🚀欢迎来到本文🚀
🍉个人简介：陈童学哦，目前正在学习C/C++、Java、算法等方向，一个正在慢慢前行的普通人。
🏀系列专栏：陈童学的日记
💡其他专栏：C++STL，感兴趣小伙伴可以了解一下哦
🎁希望各位→点赞👍 + 收藏⭐️ + 留言📝 ​
⛱️万物随心起，心动则万物动🤺

前言

因参加了我校的ACM暑期集训为之后的xcpc等赛事做准备，所以就有了此文哈哈。本文主要复盘做题的过程以及一些感悟，便于复习巩固。辣么现在废话也不多说啦，直接往下看吧哈哈。

A - 关于gcd

来源：洛谷P4549 【模板】裴蜀定理
算法标签：数学、最大公约数、gcd不定方程

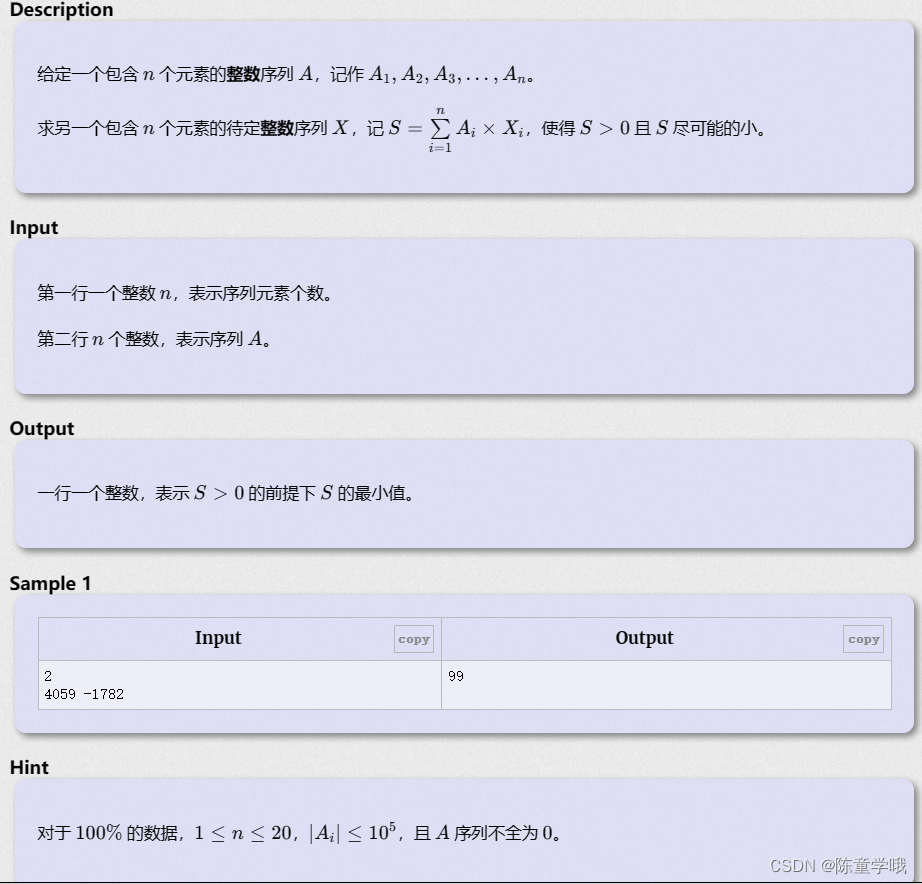
解题思路

这题要用到裴蜀定理(或称贝祖定理)，那么这个勾八定理是干啥的，怎么用呢？它其实就是二元一次方程ax+by=c存在整数解时c应为a、b的最小公约数。但是这里要注意将负数变为正后再求。

示例代码

#include<bits/stdc++.h>
using namespace std;
int n,a,res;
int gcd(int x,int y)
{return !y?x:gcd(y,x%y); 辗转相除法求最大公约数
}
int main()
{cin>>n;for(int i=1;i<=n;i++){cin>>a;a=a>0?a:-a;res=gcd(res,a);}cout<<res;
}

B - gcd区间

来源：洛谷P1890 gcd区间
算法标签：数学

解题思路

这题就是求所给区间的最大公约数，我看有大佬用线段树做的（但是我不会哈哈），我用动规思想做的

示例代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a,b,k[1005][1005],d,p;
int main()
{cin>>a>>b;for(int i=1;i<=a;i++)cin>>k[i][i];for(int i=a-1;i>=1;i--)for(int j=i+1;j<=a;j++)k[i][j]=__gcd(k[i][i],k[i+1][j]);for(int i=1;i<=b;i++){cin>>d>>p;cout<<k[d][p]<<endl;}		}

C - Cipher Shifer

来源：CodeforcesA. Cipher Shifer

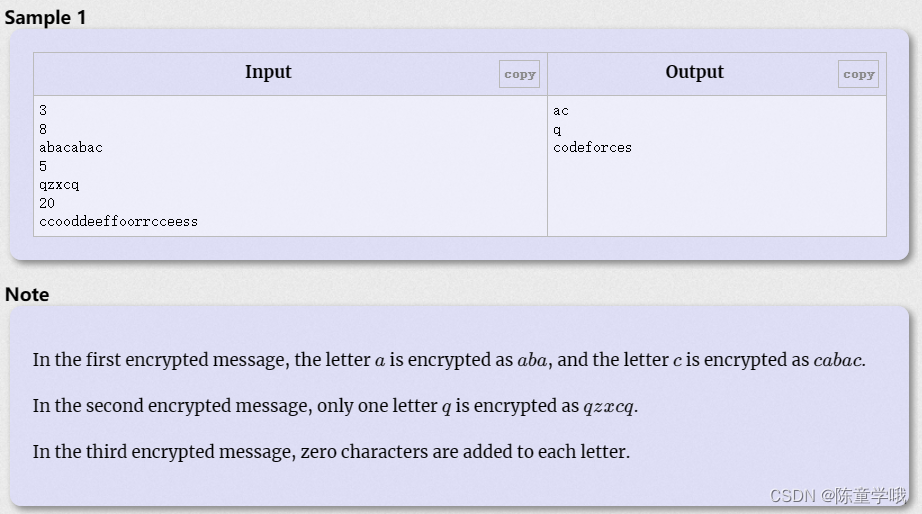
解题思路

遍历字符串并更新字符即可

示例代码

#include<bits/stdc++.h>
using namespace std;
int main()
{int t,n;cin>>t;for(int i=0;i<t;i++){cin>>n;char c[110],b;cin>>c;b=c[0];for(int j=1;j<n;j++){if(b==c[j]){cout<<c[j];j++;b=c[j];}}if(i!=t-1)cout<<endl;}
}

D - 质数筛

来源：洛谷P5736 【深基7.例2】质数筛

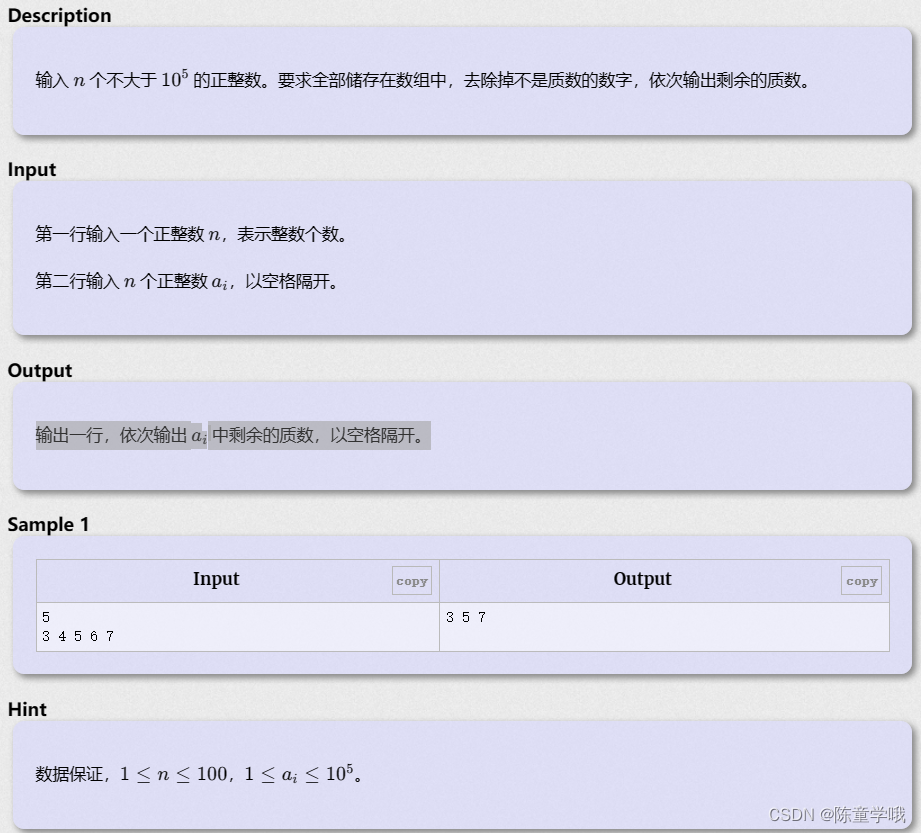
解题思路

这题其实写个判断素数的函数就OK了，对啦，质数就是素数哦！

示例代码

#include<bits/stdc++.h>
using namespace std;
int n,m;
bool judge(int x)
{if(x<=1)return false;for(int i=2;i<=sqrt(x);i++){if(x%i==0)return false;}return true;
}
int main()
{cin>>n;for(int i=1;i<=n;i++){cin>>m;if(judge(m))cout<<m<<" ";}
}

E - 完全平方数

来源：洛谷P8754 [蓝桥杯 2021 省 AB2] 完全平方数
算法标签：数论、素数判断、质数、筛法

解题思路

完全平方数想必大家都听过撒，而完全平方数有一个性质：完全平方数的质因子的指数一定为偶数。
什么意思呢？如：36=2^2 x 3^2= 6^2

示例代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,x=1;
int main()
{cin>>n;for(ll i=2;i*i<=n;i++){int cnt=0;while(n%i==0)cnt++,n/=i;if(cnt%2==1)x*=i;}x*=n;cout<<x;
}

F - Vika and Her Friends

来源：CodeforcesA. Vika and Her Friends

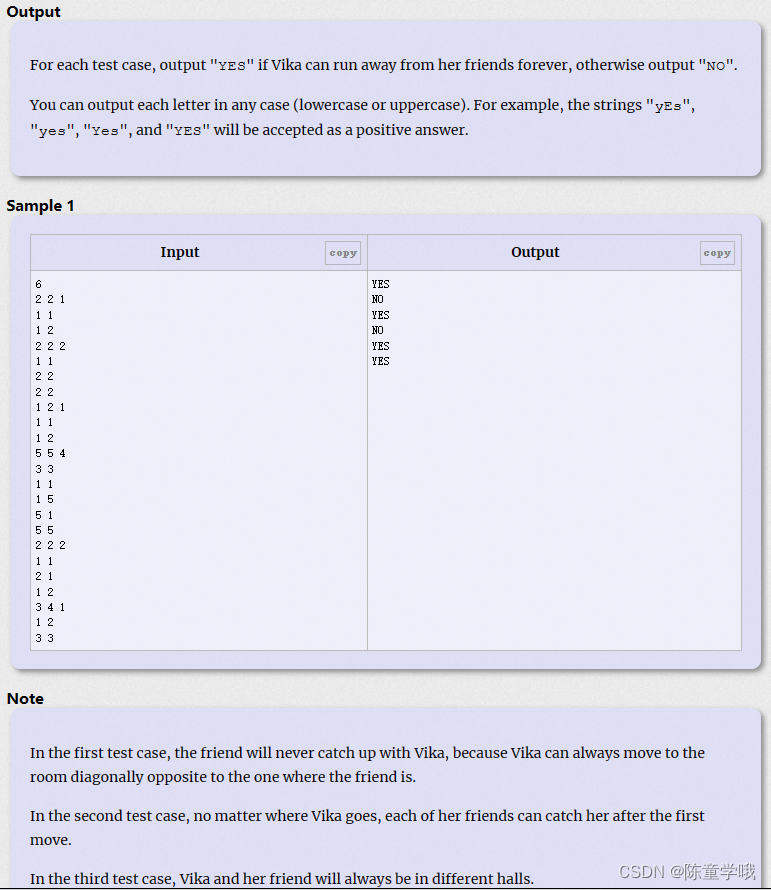
解题思路

如果距离为奇数，那么就抓不住Vika，只有为偶数时才能抓住（我也不知道怎么说啦）

示例代码

#include<bits/stdc++.h>
using namespace std;
int t;
int n,m,k;
int x,y,a,b,flag;
int main()
{	cin>>t;while(t--){flag=0;cin>>n>>m>>k>>x>>y;for(int i=0;i<k;i++){cin>>a>>b;if((abs(x-a)+abs(y-b))%2==0)flag=1;}if(flag)printf("NO\n");elseprintf("YES\n");}
}

总结

ADay5的题主要是数论的题。
算法：数论、最大公约数
感悟：想要学好算法，数学还是不能落下的呀（手动哭脸）
总结：数论的题偏数学里的解题思路