提出问题
在STM32——直流电机PI调速一文中推导了直流有刷电机的数学模型,在不考虑电流环的情况下,可做降阶处理,视同一个一阶系统,通过简单的 P I PI PI控制使得电机有着不错的响应,但仍然存在两个问题,一是参数整定依托数学模型,较为繁琐,二是没有电流环,系统性能欠佳。例如:某电机输入电压 U ( v ) U(v) U(v)与转速 n ( n / m i n ) n(n/min) n(n/min)之间的传递函数为

我们期望系统响应快,超调小,令ts = 0.4 s , ξ = 0.9 =0.4s,ξ=0.9 =0.4s,ξ=0.9,在前文计算 P I PI PI控制器参数的基础上为消除闭环零点的影响做略微调整,得控制器如下:
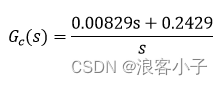
假设系统中存在干扰,整体框图如下:
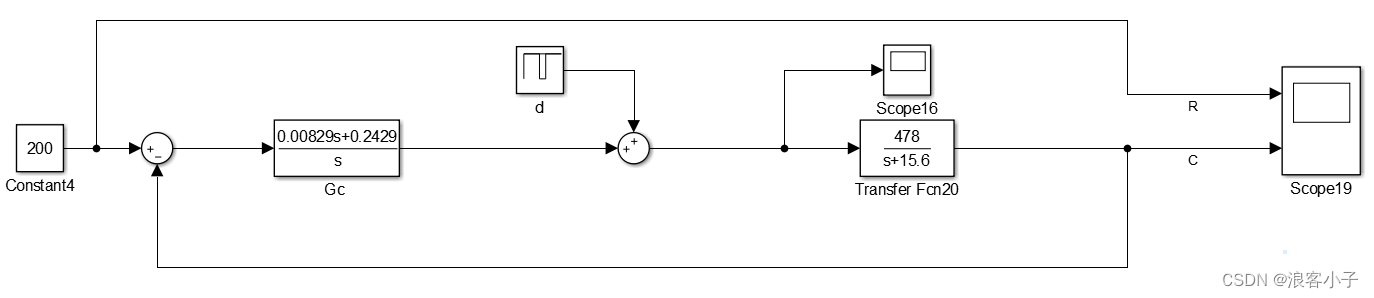
干扰 d d d在 0.9 − 1.2 s 0.9-1.2s 0.9−1.2s内输出 − 5 -5 −5,其余时间为 0 0 0。得系统响应如下图所示
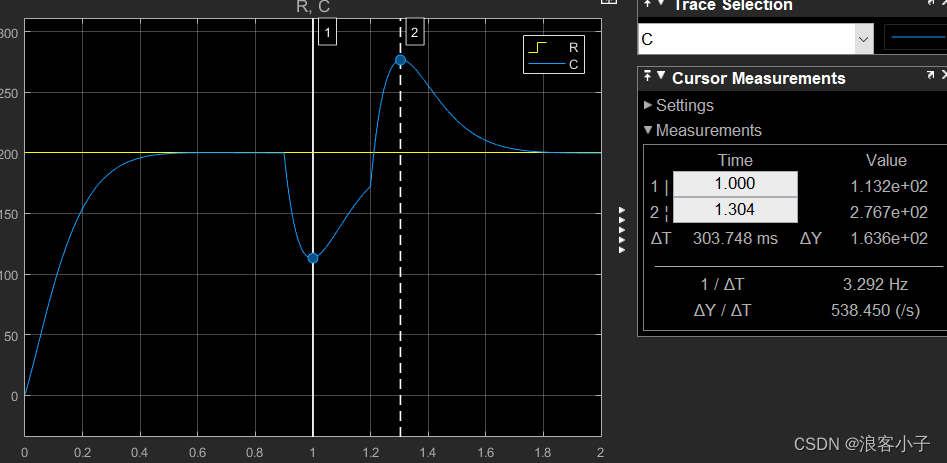
可见,系统的波动幅度很大,两个峰值之间的差为 163.6 163.6 163.6,很明显,这样的系统抗干扰能力就很差了,电机的机械特性较软,加电流环就能得到改善,电流环控制的是电流,其实是转矩,所以电机的机械特性较硬。
电流环在电机控制中很重要,对电机的性能有很大的影响,从控制理论的角度看,我们的目的是控制电机的转速或者位置,电流环相当于给系统增加了一个内环,使得系统更加稳定,增大了系统性能提升的空间。但增加一个电流环无论是从硬件上还是软件上,都是比较麻烦的,在不知道电机内部参数的情况下想要调好电流环也不是一件容易的事,那么有没有一种办法在不要电流环的情况下仍能保证系统的性能和鲁棒性不会受到太大影响,而且更方便参数整定呢?
前面说到,电流环是用输出转矩去抵消系统中的干扰,因为干扰的存在直接影响转速,那我们可以利用转速作为反馈信号使输入电压快速克服掉干扰,也就是说,转速受干扰影响减小时,通过快速增大电机输入电压来增大转速,反之减小输入电压。利用局部反馈的方式就能很好的做到这点。
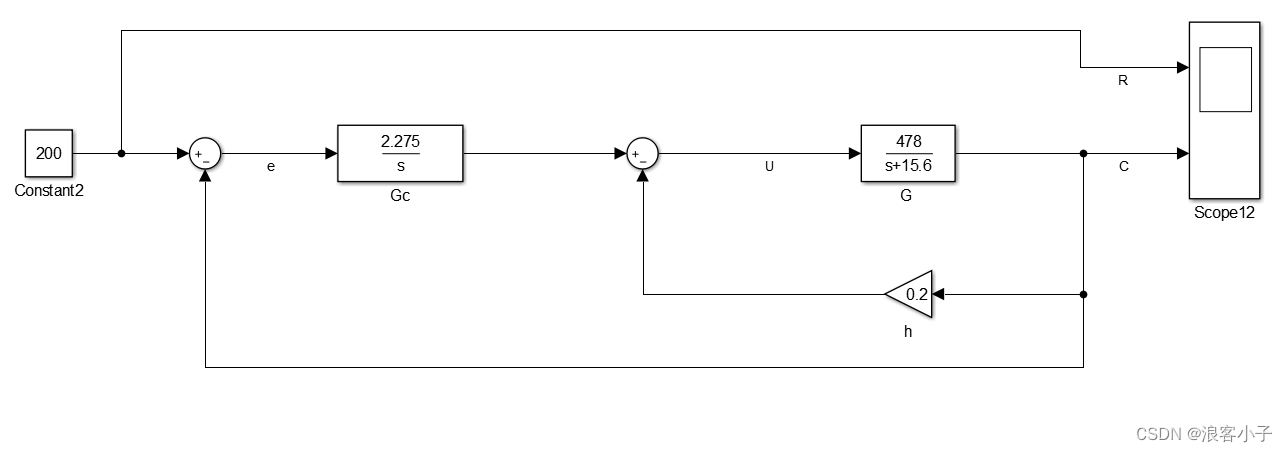
局部反馈
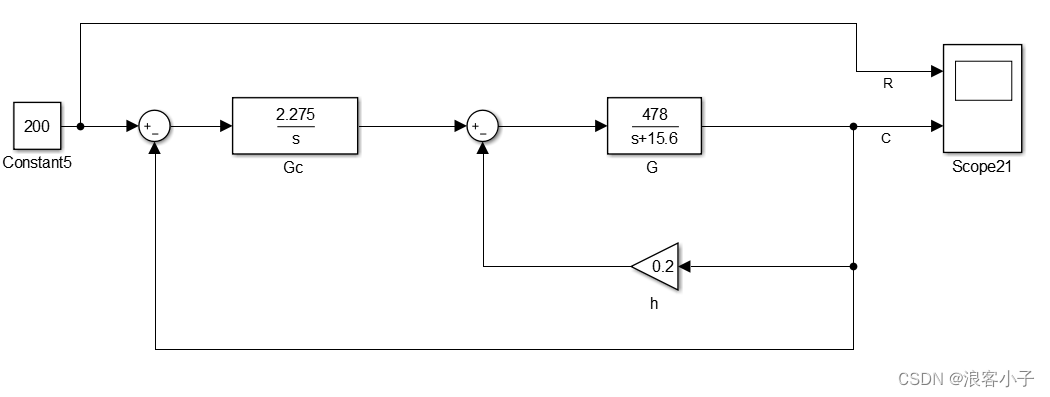
上图便是局部反馈的系统结构图, G G G表示电机传递函数, G c G_c Gc表示控制器,为了方便·参数整定,积分控制就够了, h h h表示反馈系数,如果将上图中的局部反馈在化简掉,得到一个新的被控对象 G p ( s ) G_p(s) Gp(s)
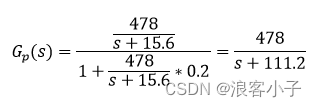
所以上面的结构框图可以等效为
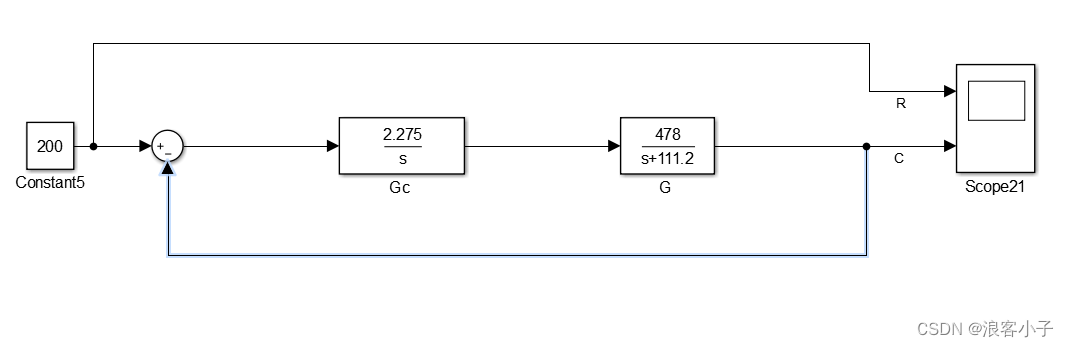
通过对比 G ( s ) G(s) G(s)和 G p ( s ) G_p(s) Gp(s)可以看出,局部反馈相当于将原系统的极点放大了,极点越大越远离虚轴,响应越快,对主导极点的影响越小。
抗扰性
我们先来看看局部反馈与 P I PI PI控制的效果,在同样系统指标与干扰影响下
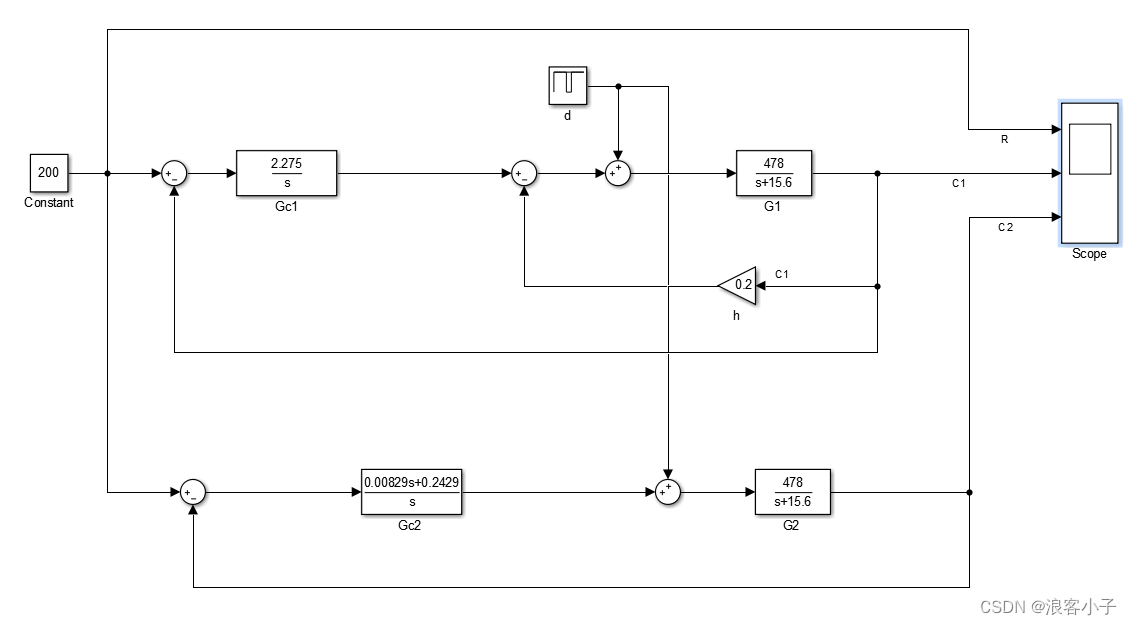
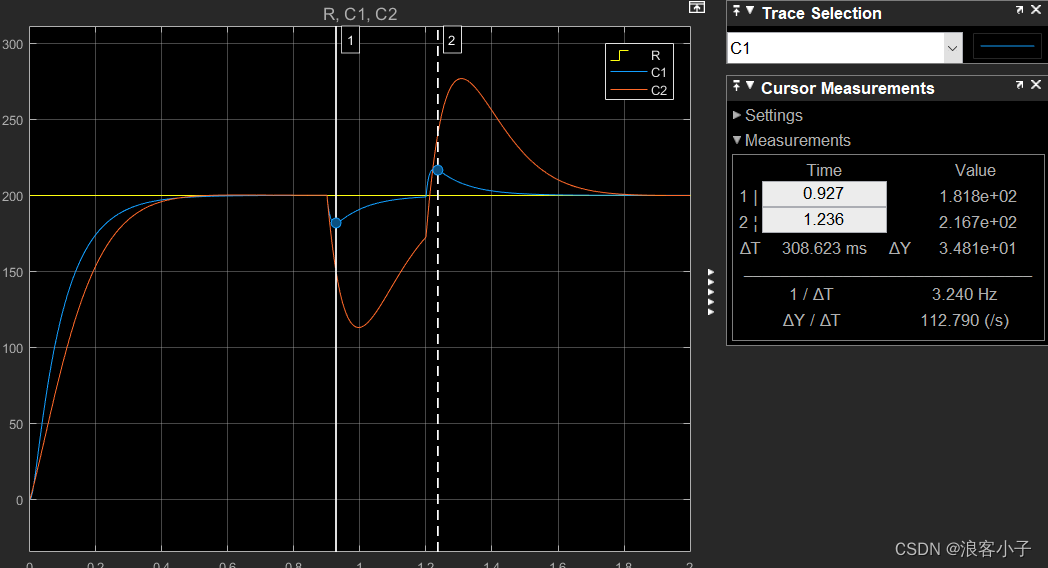
可见,局部反馈的方式能明显抑制系统波动,两个峰值之差只有 34.8 34.8 34.8。
鲁棒性
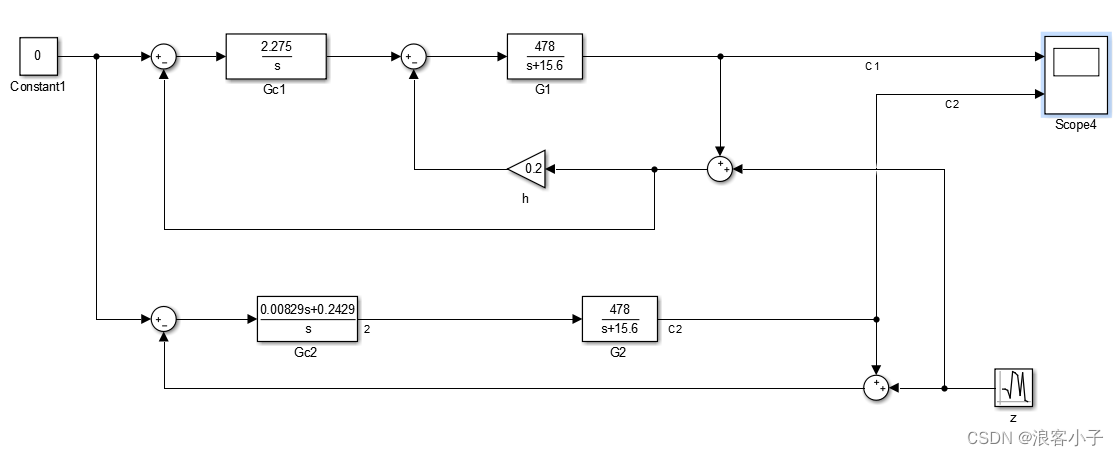
电机在不同负载下,它的传递函数的参数会发生改变,假设在某个负载下,电机的传递函数变为

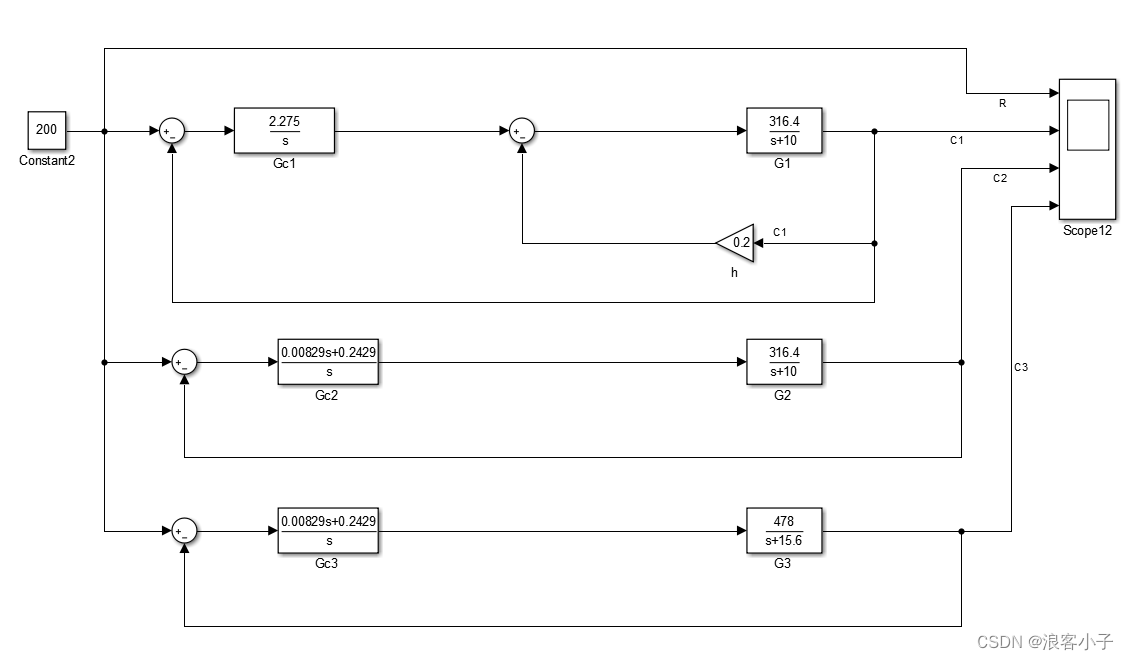
为了更好地对比,加入参数不变情况下的 P I PI PI控制,其中 C 1 、 C 2 、 C 3 C1、C2、C3 C1、C2、C3分别表示变系统参数后的局部反馈控制、变系统参数后的 P I PI PI控制、原系统的 P I PI PI控制,波形如下
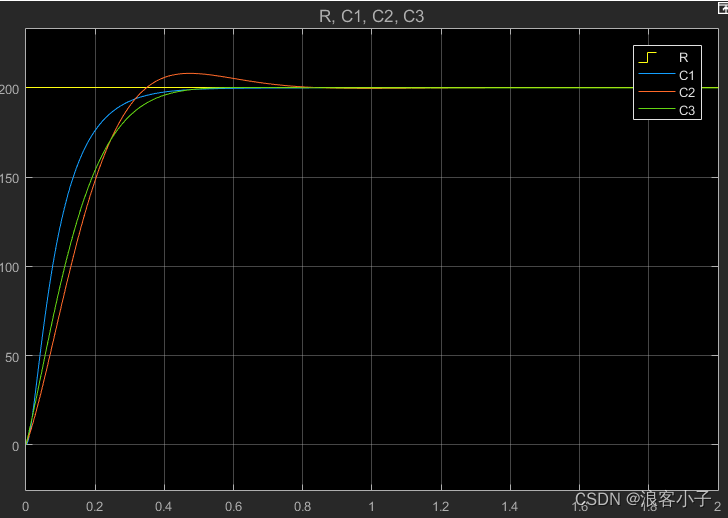
从图中可以看出,变系统参数后的局部反馈控制几乎没有太大的影响,而变系统参数后的 P I PI PI控制有了一个明显的超调,而且调节时间大大的延长了。
参数计算
前述的理论证明不做详细赘述,只解释积分系数和反馈系数怎么计算。对于一阶系统,其结构为
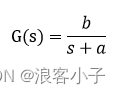
参数 b 、 a b、a b、a之间存在 b = K a b=Ka b=Ka的关系,其中 K K K表示开环增益。在直流有刷电机中,同样有 n ( ∞ ) = K U n(∞)=KU n(∞)=KU, n ( ∞ ) n(∞) n(∞)表示在电压 U U U下的稳态转速,利用这个关系便可以得到直流有刷电机的开环增益,在测量时可多测量几组数据求平均值。
加入局部反馈后,反馈系数 h h h与原系统传递函数 G ( s ) G(s) G(s)组成新的被控对象 G p ( s ) G_p(s) Gp(s)
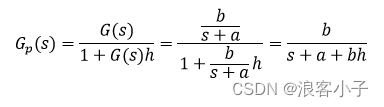
取 a + b h > 5 a a+bh>5a a+bh>5a即可,有
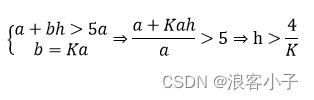
再说积分系数 K i K_i Ki,由于只用积分控制,而且 G p ( s ) G_p(s) Gp(s)的极点足够大,所以闭环传递函数Gclose(s)仍然可视作一个一阶系统,结构如下:
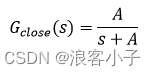
调节时间 t s t_s ts与 A A A之间的关系为

接着计算 G p ( s ) Gp(s) Gp(s)的开环增益 K k K_k Kk
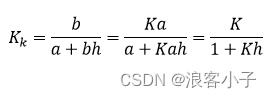
最后 K i K_i Ki为

总结后公式如下:

我们原系统中, a = 15.6 , b = 478 a=15.6,b=478 a=15.6,b=478,取 t s = 0.4 s t_s=0.4s ts=0.4s( t s t_s ts在取值时不能选择的太小,它是有上限的,这个上限 U p = 3.912 / a Up=3.912/a Up=3.912/a)。
第一步:计算开环增益 K K K

第二步:计算反馈系数 h h h( h h h不要取得太大)
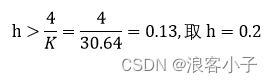
第三部:计算 K i K_i Ki
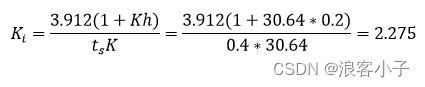
算法表达式
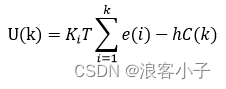
其中 T T T表示采样时间。
缺点
通过上述可知,局部反馈控制具有较强的抗干扰能力和鲁棒性,参数整定也较为简单,但有个缺点,就是无法抑制测量噪声,和 P I PI PI控制对比一下
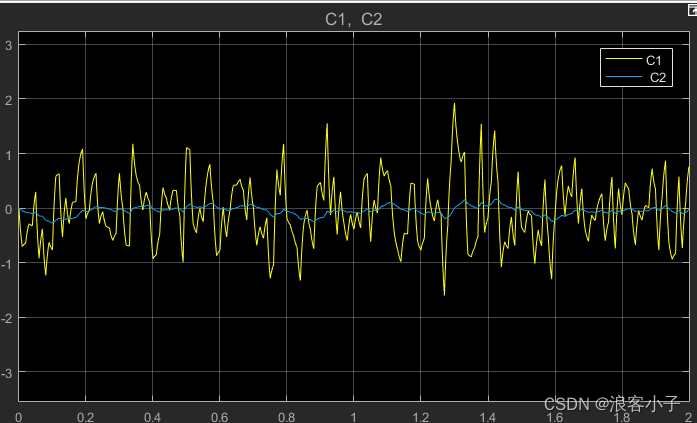
从上图可知,局部反馈控制在抑制测量噪声上不如 P I PI PI控制,所以电机的编码器分辨率不要太小,否则电机进入稳态后会有很多毛刺。


C卷 (JavaPythonC++Node.jsswift))










![【算法每日一练]-动态规划(保姆级教程 篇14) #三倍经验 #散步 #异或和 #抽奖概率](http://pic.xiahunao.cn/【算法每日一练]-动态规划(保姆级教程 篇14) #三倍经验 #散步 #异或和 #抽奖概率)


获取商品的图片信息)


