汉诺塔问题

问题：

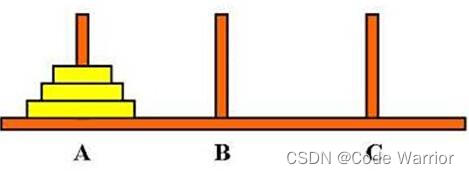
Hanoi(汉诺)塔问题。这时一个古典的数学问题，是一个递归方法解题的典型例子。问题是这样的：古代有一个梵塔，塔内有3个座 A,B,C（如下图）。开始时A座上有64个盘子，盘子大小不等，大的在下，小的在上。有一个老和尚想把这64个盘子从A座移到C座，但规定每次只允许移动一个盘，且在移动过程中3个座上都始终保持大盘在下，小盘在上。在移动过程中可以利用B座。要求编程序输出移动盘子的步骤。

解题思路：

要把64个盘子从A座移动到C座，一般人是不可能确定怎么移动盘子的每一个具体步骤的。所以我们需要找到一个解决问题的办法，把看似简单的问题简单化，使问题得以迎刃而解。

我们可以将63个盘子移动到B座，然后将A座的盘子移动到C座，这时就把移动64个盘子的问题简化为移动63个盘子，难度减小了一些。但是我们怎么才能将63个盘子从A座移到B座？

要想将63个盘子移动到B座，我们只需将62个盘子移动到C座，再将A座的一个盘子移动到B座。这时的问题又转换为如何将62个盘子移动到C座。

要想将62个盘子移动到C座，我们只需将61个盘子移动到B座，再将A座的一个盘子移动到C座。这时的问题又转换为如何将61个盘子移动到B座。

......

这样层层递归下去，问题就简单很多了，只要有足够的时间就可以以最少的步骤将A座的盘子移动到C座了。

思路实践：

为了更好理解递归在此问题的运用，我们可以将A,B,C的三个座分为起始塔，中转塔，目标塔。下面我们将试着移动四个盘子。

1. A座前三个盘子移动到B座

要想将这三个盘子移动到B座，我们应该先将前两个盘子移动到C座，而要想把前两个盘子移动到C座，我们应该先将前一个盘子移动到B座。这时我们逆着推回去就可以得到这里移动的整个步骤：

A -> B（第一个盘子移动到了B座）

A -> C（第二个盘子移动到了C座）

B -> C（B座的盘子移动了到C座）

其中将前两盘子从A座移动到C座是以A座为起始塔，B为中转塔，C为目标塔进行的移动。

A -> B(第三个盘子移动到了B座）

最后需要将C座的两个盘子移动到B座，这时就以C座为起始塔，A为中转塔，B为目标塔进行移动，跟上面移动两个盘子相比不同的就是将A换为C,B换为A,C换为B,那么这里的移动步骤就是：

C -> A, C -> B, A -> B。

综上，这一步的移动步骤为：A -> B, A -> C, B -> C, A -> B, C -> A, C -> B, A -> B

2. A座最后一个盘子移动到C座（A -> C）

3. B座的三个盘子移动到C座

由1可知A座前三个盘子移动到座的移动步骤为：

A -> B, A -> C, B -> C, A -> B, C -> A, C -> B, A -> B

我们可以知道第一步1是以A座位起始塔，C位中转塔，B位目标塔进行三个盘子的移动，而第3步是以B座为起始塔，A座为中转塔，C座为目标塔进行三个盘子的移动，以此可以知道第三步的步骤为：B->C B->A C->A B->C A->B A->C B->C

综上，移动四个盘子的完整步骤就为：

A->B A->C B->C A->B C->A C->B A->B A->C B->C B->A C->A B->C A->B A->C B->C

假设A座有n个盘子，从上面的移动步骤我们可以知道盘子的移动可以分为三步：

1. 把起始塔的前n-1个盘子放到中转塔上。

(1). 把起始塔的前n-2个盘子放到中转塔上。

......

(2). 然后把起始塔的一个盘子放到目标塔上。

(3). 最后中转塔的n-2个盘子放到目标塔上。

......

2. 然后把起始塔的一个盘子放到目标塔上。

3. 最后把中转塔的n-1个盘子放到目标塔上。

(1). 把起始塔（前一步的中转塔）的前n-2个盘子放到中转塔上。

......

(2). 然后把起始塔的一个盘子放到目标塔上。

(3). 最后中转塔的n-2个盘子放到目标塔上。

......

就这样层层递归下去我们就可以得到一个完整的步骤了。

代码分析：

写一个move函数表示盘子从x座移到y座的过程。写一个递归函数，根据上面的分析可知第一步是用递归将n-1个盘子移动到中转塔上，第二步是将起始塔的一个盘子移动到目标塔上，第三步是用递归将中转塔上的盘子移动到目标塔上，当n==1（也就是A座还有一个盘子时）结束递归，其中我们只需要将确定递归的最后一步的步骤就可以写出这个递归函数了，比如第一个递归是将n-1个盘子移动到中转塔上，那它递归到最后面就是将A座的第一个盘子移动到B座上，所以递归就写成Hanoi(n - 1, a, c, b);

完整代码：

void move(char x,char y)
{printf(" %c->%c ", x, y);
}
void Hanoi(int n, char a, char b, char c)
{if (n == 1){move(a, c);}else{Hanoi(n - 1, a, c, b);move(a, c);Hanoi(n - 1, b, a, c);}
}
int main()
{int n = 0;printf("请输入盘子的数量>:");scanf("%d", &n);Hanoi(n, 'A', 'B', 'C');return 0;
}

A座上一开始放四个盘子时，移动盘子的步骤：