目录
引入
并查集的具体讲解及代码实现
Quick Find
Quick Union
基于size的优化
代码实现
基于rank的优化
代码实现
路径压缩
代码实现
更多关于路径压缩的并查集
引入
由孩子指向父亲的这种特殊的树结构可以很高效的处理连接问题,在一个复杂的图中(如下图),给出图中任意两点,问它俩之间是否存在一条连接它俩的路径。

在并查集中,主要有合并集合以及判断是否连接两个动作,即“并”和“查”。

并查集的具体讲解及代码实现
//接口
public interface UF {//不考虑向并查集中添加元素或者删除元素int getSize();//判断是否相连boolean isConnected(int p, int q);//两个元素合并在一起,变成一个集合中的元素void unionElements(int p, int q);
}
Quick Find
相同id值的数字属于同一个集合,如下图,0、2、4、6、8是同一个集合,1、3、5、7、9是同一个集合。
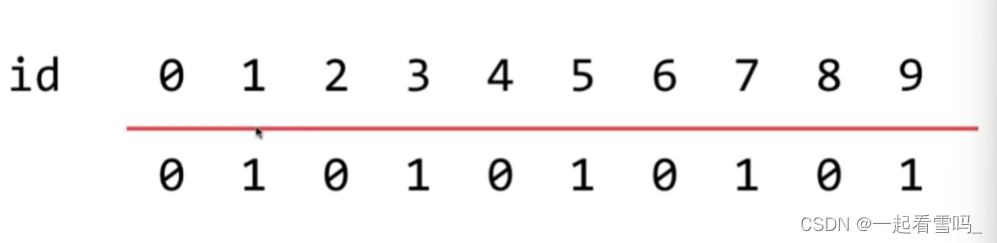
我们用数组存储id值可以很容易的实现isConnected(int p, int q)这个“查”的操作,也就是转换成查找p、q的id值是否相等,即find(p) == find(q) ? 这个find操作的时间复杂度为O(1),非常快,我们叫做Quick Find。
“查”了解完了,那“并”呢?如果我们想合并1和4又该怎么操作呢。原本1 3 5 7 9是连接起来的,0 2 4 6 8是连接的,一旦我们把1和4连接起来,那么所有和1、4连接的元素也就都连接起来了。在我们上图的例子中我们所有的元素所对应的id值就应该改成一样的,都取0或1,具体都改成0还是都改成1是无所谓的,在这里我们选择都改为1。
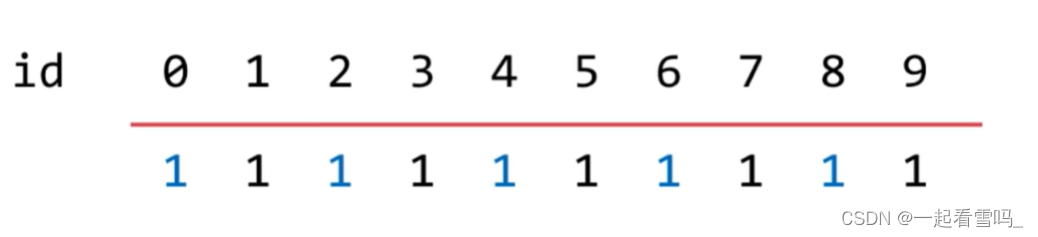
我们通过循环的方式把0都改为1,这个Union的操作时间复杂度为O(n) 。
//第一版的并查集
public class UnionFind1 implements UF{private int[] id;public UnionFind1(int size){id = new int [size];//每一个元素对应的集合编号都不一样,表示所属不同的集合,各不相连for(int i = 0; i < id.length; i++){id[i] = i;}}@Override public int getSize(){return id.length;}//查找元素p所对应的集合的编号//由于这个方法不在接口中,所以我们设为private的private int find(int p){if(p < 0 || p >= id.length){throw new IllegalArgumentException("p is out of bound.");}return id[p];}@Overridepublic boolean isConnected(int p, int q){return find(p) == find(q);}@Overridepublic void unionElements(int p, int q){int pID = find(p);int qID = find(q);if(pID == qID){return;}for(int i = 0; i < id.length; i++){if(id[i] == pID){id[i] = qID;}}}
}

Quick Union
这一版的并查集是一般情况下更常用的。由于Quick Find中的合并操作时间复杂度为O(n),所以数据规模一大的话算法就会很慢,而下面要讲的这种并查集顾名思义可以很快的合并元素,因为我们要实现一种底层逻辑,即孩子指向父亲的特殊树结构。
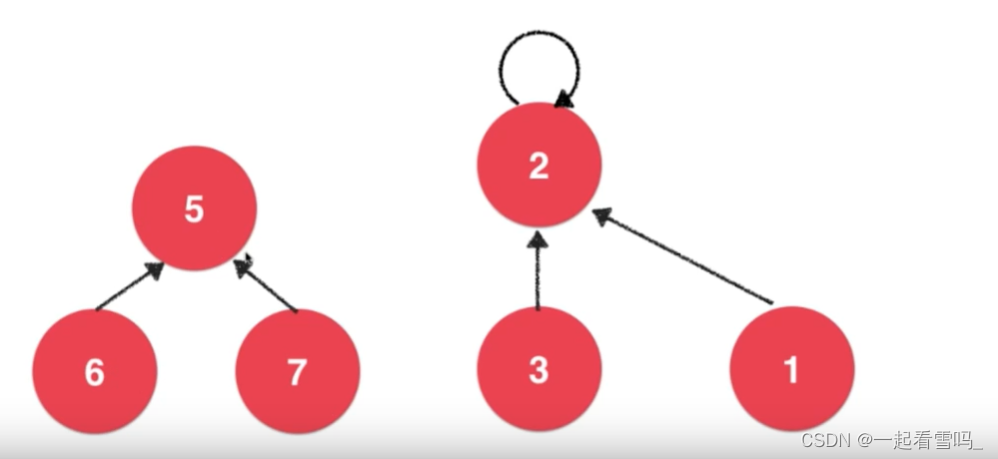
如上图,每个结点只会有一个指针指向另一个结点,结点1、2、3是相连接的,根节点为2,指向它本身。结点5、6、7是相连的,根节点为5,现在我们希望合并3和7,那么只需要将两个集合的根节点相连就好,如下图。
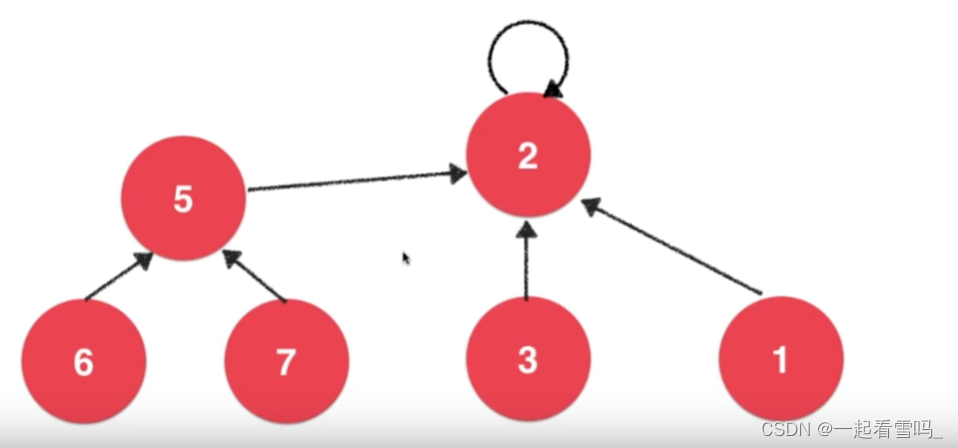
关于指针的存储,我们依然可以采取数组的方式来存储。数组就代表第i个元素的指针指向了某个结点。在初始情况下,每一个结点都是一个根节点,指向自己,没和任意元素相连。此刻不是一个树结构,而是一个森林。
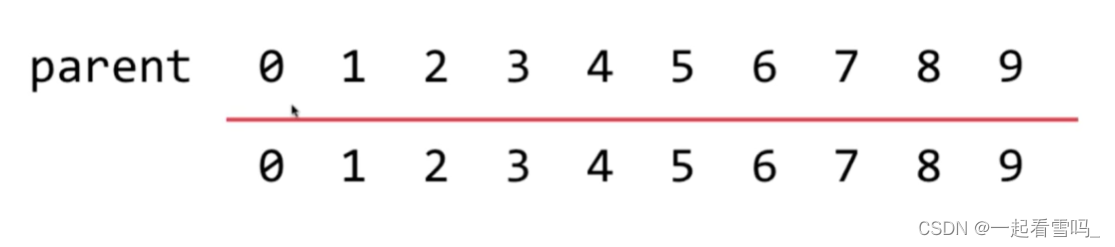
如果我们想合并4、3该怎么做呢? 很简单,就让4的指针指向3。parent数组中4的位置改为3。
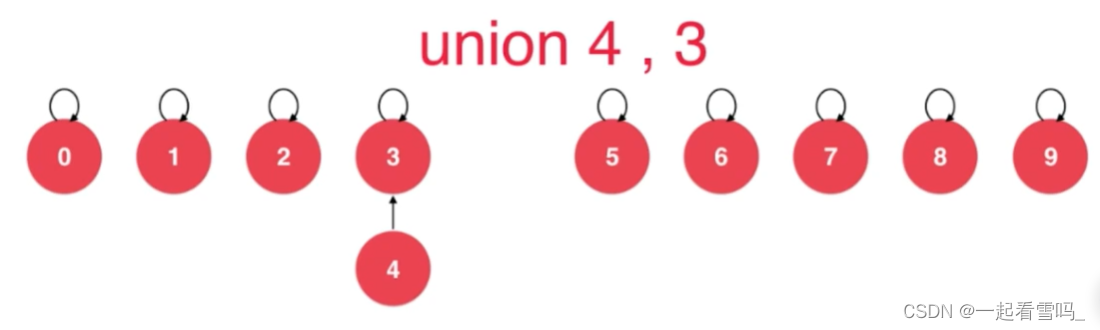
 倘若要合并两个树结构中的元素,需要这两个树结构的根节点指向根节点, 这时候就要查找哪个是根节点,即这两棵树中哪个节点是自己指向自己的。比如我们要合并9、4。
倘若要合并两个树结构中的元素,需要这两个树结构的根节点指向根节点, 这时候就要查找哪个是根节点,即这两棵树中哪个节点是自己指向自己的。比如我们要合并9、4。
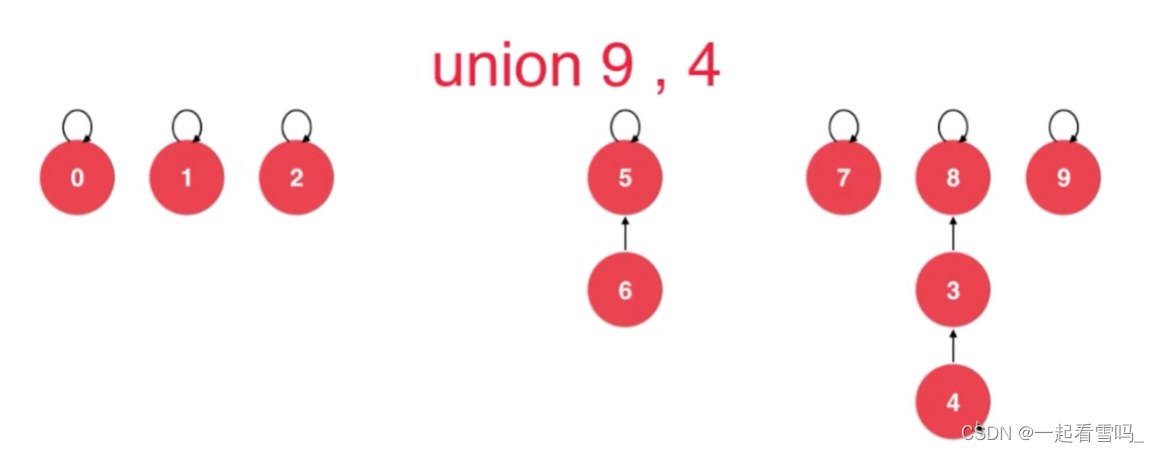
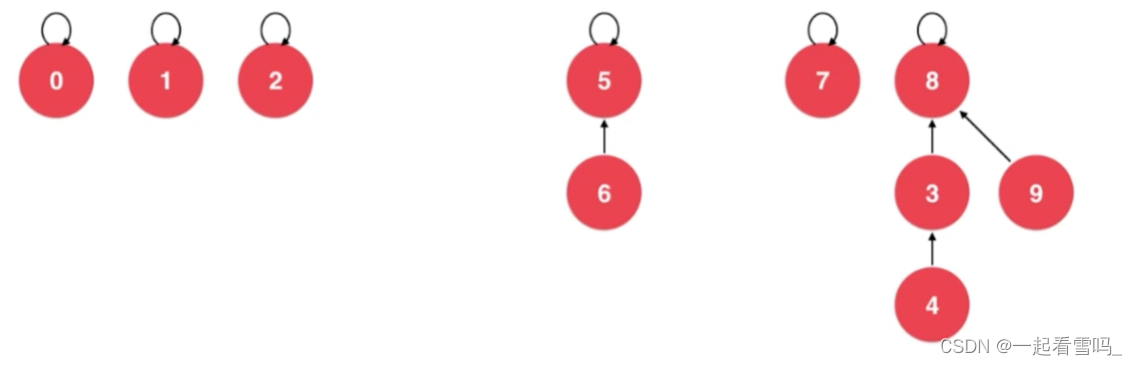 我们为什么不让9直接指向4呢?是因为如果那样做就会形成一个链表,我们树结构的优越性就不存在了。 而如果9指向4的根节点,下次我们如果要查询9这个元素所对应的根节点只需要一步查询就好了。(别忘了把parent(9) = 8~)
我们为什么不让9直接指向4呢?是因为如果那样做就会形成一个链表,我们树结构的优越性就不存在了。 而如果9指向4的根节点,下次我们如果要查询9这个元素所对应的根节点只需要一步查询就好了。(别忘了把parent(9) = 8~)
//第二版并查集
public class UnionFind2 implements UF{private int[] parent;public UnionFind2(int size){parent = new int [size];for(int i = 0; i < size; i++){parent[i] = i;}}@Overridepublic int getSize(){return parent.length;}//时间复杂度为O(h),h是树的高度//查找到数据所在的树相应的根节点private int find(int p){if(p < 0 || p >= parent.length){throw new IllegalArgumentException("p is out of bound.");}while(p != parent[p]){p = parent[p];}return p;}//时间复杂度为O(h),h是树的高度@Overridepublic boolean isConnected(int p, int q){return find(p) == find(q);}//时间复杂度为O(h),h是树的高度@Overridepublic void unionElements(int p, int q){int pRoot = find(p);int qRoot = find(q);if(pRoot == qRoot){return;}parent[pRoot] = qRoot;}
}
基于size的优化
在某些情况下,我们不判断树的形状就去合并会徒增树的高度形成一个链表的样子(如下图),我们可以考虑当前这棵树有多少个结点,即基于size来解决这个问题。
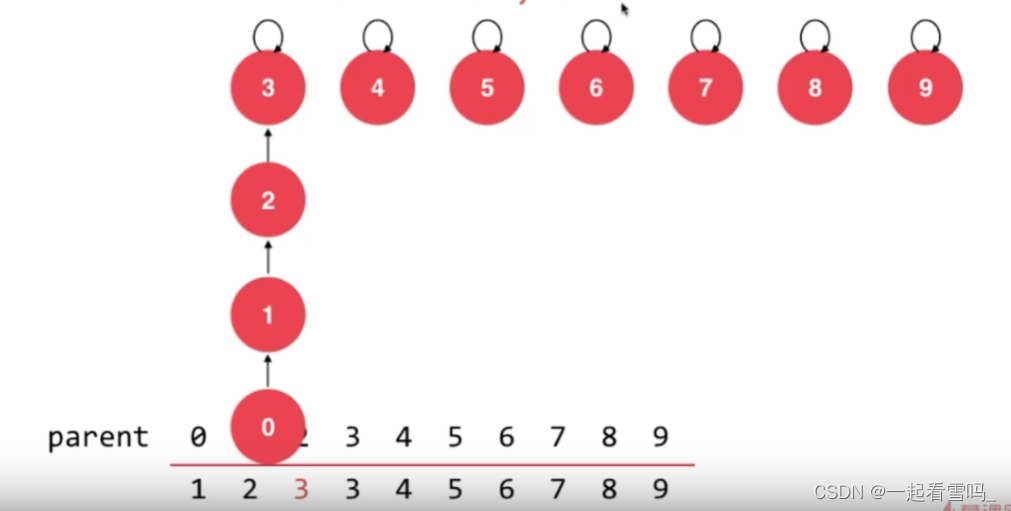
比如,我们要合并4和9。
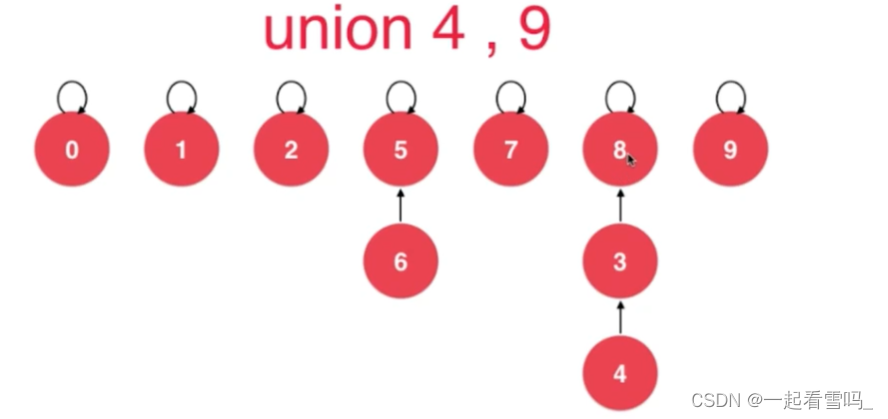
如果我们让8指向9,深度就会为4。
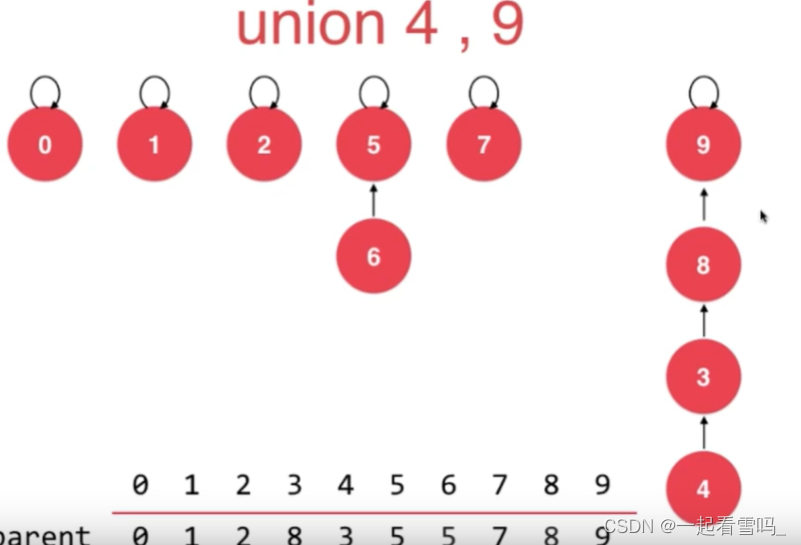
而我们让9指向8的话,树的高度只有3。

即我们让结点个数小的树指向结点个数多的树。
代码实现
//第三版的并查集
public class UnionFind3 implements UF{private int[] parent;private int[] sz; //sz[i]表示以i为根的集合中元素个数public UnionFind3(int size){parent = new int [size];sz = new int[size];for(int i = 0; i < size; i++){parent[i] = i;sz[i] = 1;}}@Overridepublic int getSize(){return parent.length;}//时间复杂度为O(h),h是树的高度//查找到数据所在的树相应的根节点private int find(int p){if(p < 0 || p >= parent.length){throw new IllegalArgumentException("p is out of bound.");}while(p != parent[p]){p = parent[p];}return p;}//时间复杂度为O(h),h是树的高度@Overridepublic boolean isConnected(int p, int q){return find(p) == find(q);}//时间复杂度为O(h),h是树的高度@Overridepublic void unionElements(int p, int q){int pRoot = find(p);int qRoot = find(q);if(pRoot == qRoot){return;}if(sz[pRoot] < sz[qRoot]){parent[pRoot] = qRoot;sz[qRoot] += sz[pRoot];}else{parent[qRoot] = pRoot;sz[pRoot] += sz[qRoot];}}
}
基于rank的优化
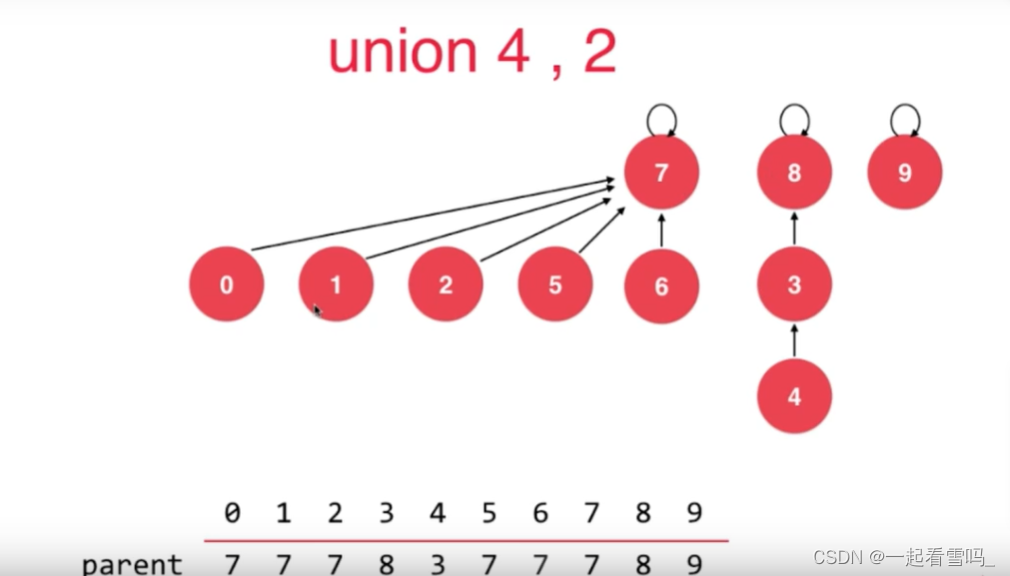
如果是基于size优化的话,结点少的指向结点多的,就会产生下图结果,树的高度变成了4。
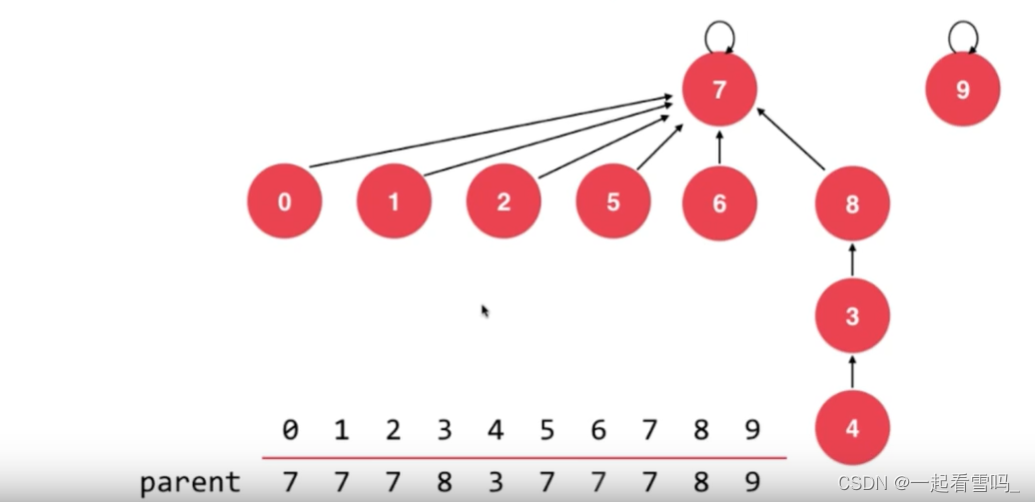
结点数少的树高度反而是高的,结点数多的这棵树高度却只有2。 所以更合理的是让7指向8。
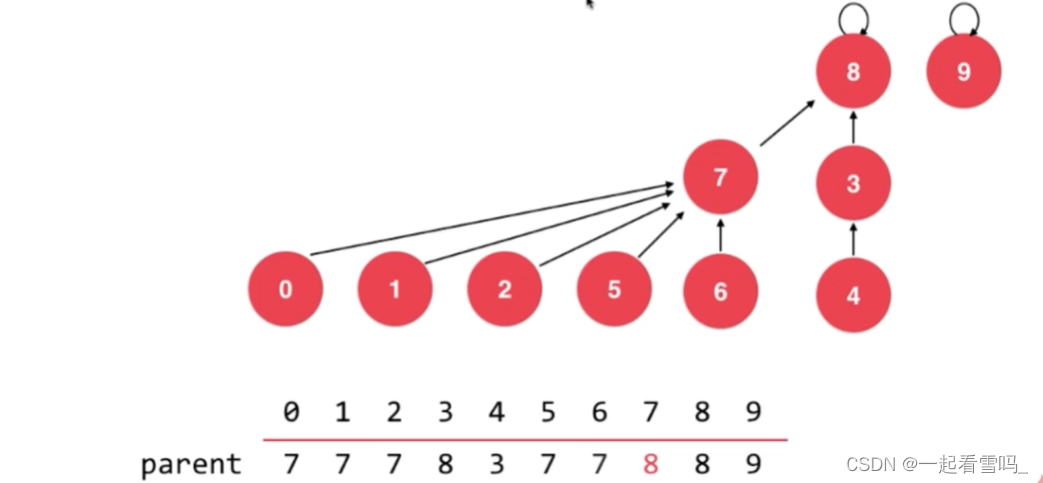
所以更合理的方法是记录一下以这个结点为根的树深度是多少,让深度比较低树指向深度比较高的树,这就是基于rank的优化。
代码实现
//第四版的并查集
public class UnionFind4 implements UF{private int[] parent;private int[] rank; //rank[i]表示以i为根的集合中树的层数public UnionFind4(int size){parent = new int [size];rank = new int[size];for(int i = 0; i < size; i++){parent[i] = i;rank[i] = 1;}}@Overridepublic int getSize(){return parent.length;}//时间复杂度为O(h),h是树的高度//查找到数据所在的树相应的根节点private int find(int p){if(p < 0 || p >= parent.length){throw new IllegalArgumentException("p is out of bound.");}while(p != parent[p]){p = parent[p];}return p;}//时间复杂度为O(h),h是树的高度@Overridepublic boolean isConnected(int p, int q){return find(p) == find(q);}//时间复杂度为O(h),h是树的高度@Overridepublic void unionElements(int p, int q){int pRoot = find(p);int qRoot = find(q);if(pRoot == qRoot){return;}if(rank[pRoot] < rank[qRoot]){parent[pRoot] = qRoot;}else if(rank[qRoot] < rank[pRoot]){parent[qRoot] = pRoot;}//相等时谁指向谁都可以else{parent[qRoot] = pRoot;rank[pRoot] += 1;}}
}
路径压缩

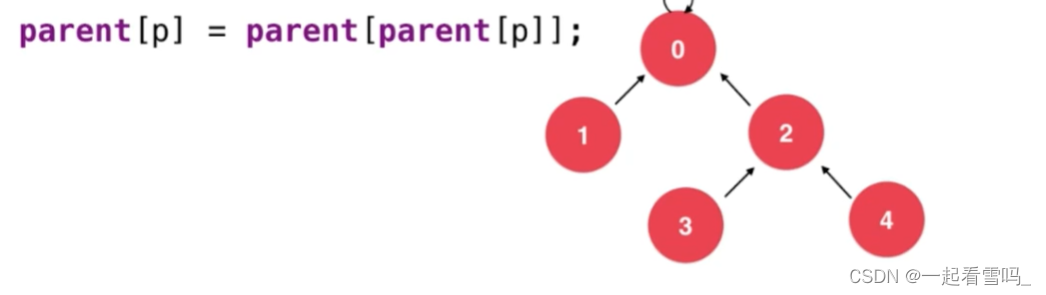
如上图所示相同效力的三种树,深度不同效率是不同的。路径压缩就是把一棵比较高的树变成比较矮的树。我们把路径压缩放在find方法中,比如我们要查找4的根节点,即find(4)。
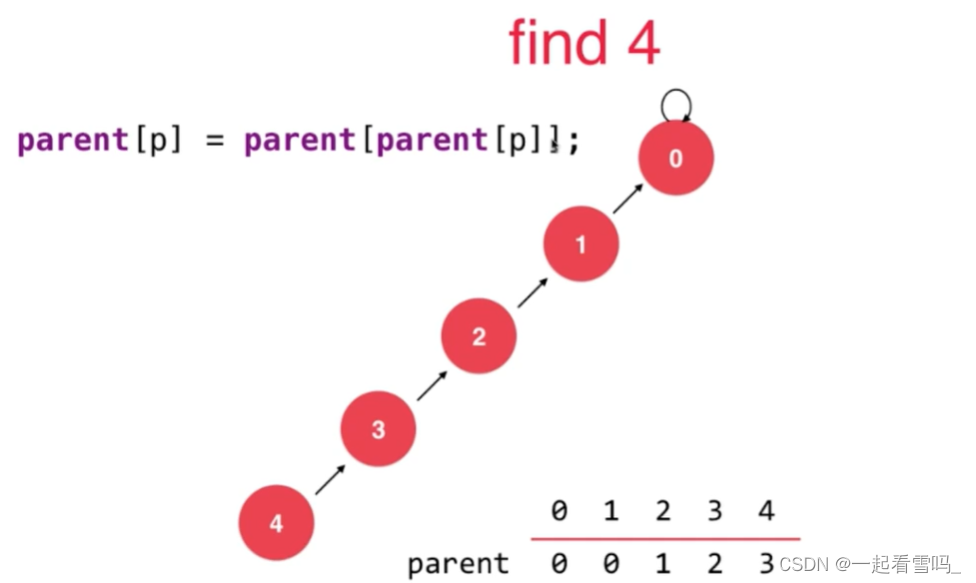
我们可以使用图上那句代码, 即把p结点的父亲的父亲设为p结点的父亲,如下图。树的深度就降低了。
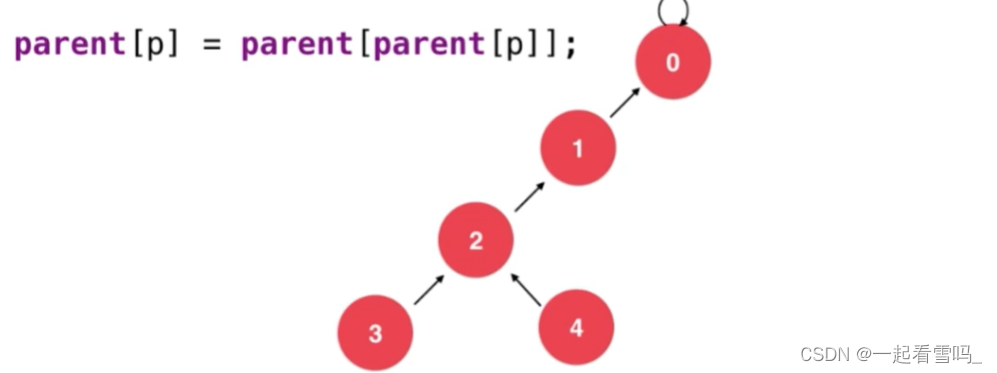
然后我们从2开始,以此类推,得到下图。 把深度从5降成3,这就是路径压缩。
代码实现
//第五版的并查集
public class UnionFind5 implements UF{private int[] parent;private int[] rank; //rank[i]表示以i为根的集合中树的层数public UnionFind5(int size){parent = new int [size];rank = new int[size];for(int i = 0; i < size; i++){parent[i] = i;rank[i] = 1;}}@Overridepublic int getSize(){return parent.length;}//时间复杂度为O(h),h是树的高度//查找到数据所在的树相应的根节点private int find(int p){if(p < 0 || p >= parent.length){throw new IllegalArgumentException("p is out of bound.");}while(p != parent[p]){parent[p] = parent[parent[p]];p = parent[p];}return p;}//时间复杂度为O(h),h是树的高度@Overridepublic boolean isConnected(int p, int q){return find(p) == find(q);}//时间复杂度为O(h),h是树的高度@Overridepublic void unionElements(int p, int q){int pRoot = find(p);int qRoot = find(q);if(pRoot == qRoot){return;}if(rank[pRoot] < rank[qRoot]){parent[pRoot] = qRoot;}else if(rank[qRoot] < rank[pRoot]){parent[qRoot] = pRoot;}//相等时谁指向谁都可以else{parent[qRoot] = pRoot;rank[pRoot] += 1;}}
}
我们添加上路径压缩后,rank没有跟着维护深度没有问题,rank只是作为合并时的参考,它不作为树的高度值和深度值,这就是为什么它叫rank而不是depth或者length。
更多关于路径压缩的并查集
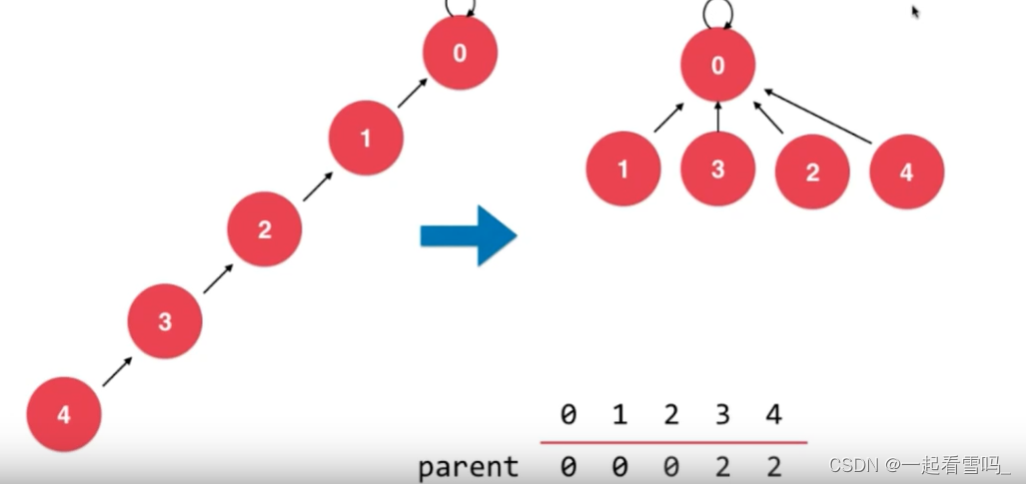
第六版本主要是为了下图的路径压缩操作一步到位,这样的方式我们要借助递归实现。
//第六版的并查集
public class UnionFind6 implements UF{private int[] parent;private int[] rank; //rank[i]表示以i为根的集合中树的层数public UnionFind6(int size){parent = new int [size];rank = new int[size];for(int i = 0; i < size; i++){parent[i] = i;rank[i] = 1;}}@Overridepublic int getSize(){return parent.length;}//时间复杂度为O(h),h是树的高度//查找到数据所在的树相应的根节点private int find(int p){if(p < 0 || p >= parent.length){throw new IllegalArgumentException("p is out of bound.");}parent[p] = find(parent[p]);return parent[p];}//时间复杂度为O(h),h是树的高度@Overridepublic boolean isConnected(int p, int q){return find(p) == find(q);}//时间复杂度为O(h),h是树的高度@Overridepublic void unionElements(int p, int q){int pRoot = find(p);int qRoot = find(q);if(pRoot == qRoot){return;}if(rank[pRoot] < rank[qRoot]){parent[pRoot] = qRoot;}else if(rank[qRoot] < rank[pRoot]){parent[qRoot] = pRoot;}//相等时谁指向谁都可以else{parent[qRoot] = pRoot;rank[pRoot] += 1;}}
}
第六版路径压缩比第五版性能上整体差一点点,递归需要额外的消耗,参加算法竞赛不要忘了路径压缩提高性能哦!


)

:VLAN的配置)







)



)

)
