【数据结构和算法】相等行列对

其他系列文章导航

Java基础合集
数据结构与算法合集

设计模式合集

多线程合集

分布式合集

ES合集

文章目录

其他系列文章导航

文章目录

前言

一、题目描述

二、题解

2.1 三层循环

2.2 哈希 + 二层循环

三、代码

3.1 三层循环

3.2 哈希 + 二层循环

四、复杂度分析

4.1 三层循环

4.2 哈希 + 二层循环

前言

这是力扣的 2352 题，难度为中等，解题方案有很多种，本文讲解我认为最奇妙的一种。

一、题目描述

给你一个下标从 0 开始、大小为 n x n 的整数矩阵 grid ，返回满足 Ri 行和 Cj 列相等的行列对 (Ri, Cj) 的数目。

如果行和列以相同的顺序包含相同的元素（即相等的数组），则认为二者是相等的。

示例 1：

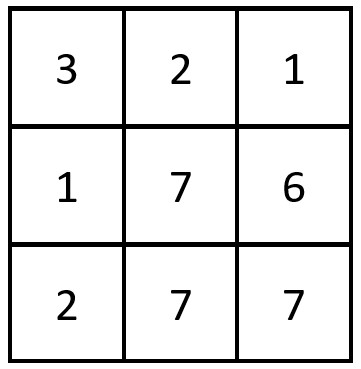
输入：grid = [[3,2,1],[1,7,6],[2,7,7]]
输出：1
解释：存在一对相等行列对：
- (第 2 行，第 1 列)：[2,7,7]

示例 2：

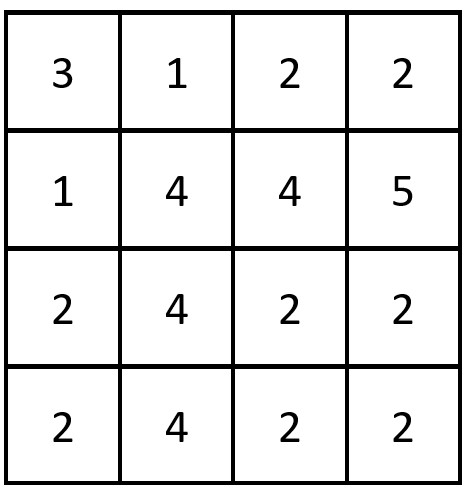
输入：grid = [[3,1,2,2],[1,4,4,5],[2,4,2,2],[2,4,2,2]]
输出：3
解释：存在三对相等行列对：
- (第 0 行，第 0 列)：[3,1,2,2]
- (第 2 行, 第 2 列)：[2,4,2,2]
- (第 3 行, 第 2 列)：[2,4,2,2]

提示：

n == grid.length == grid[i].length
1 <= n <= 200
1 <= grid[i][j] <= 105

二、题解

2.1 三层循环

思路与算法：

我们直接将矩阵 gridgridgrid 的每一行和每一列进行比较，如果相等，那么就是一对相等行列对，答案加一。

2.2 哈希 + 二层循环

思路与算法：

这道题暴力解：遍历每一列，然后遍历每一行，再比对当前行和当前列是否以相同顺序包含相同元素。

遍历每一行的时间复杂度为O(n^2)，再套上一层遍历每一列时间复杂度就为O(n^3)。

我们可以发现，我们其实在遍历每一列的时候都在重复的遍历每一行，那么我们可以使用哈希表来存储每一行的数字序列字符串。

然后在遍历每一个行的时候生成这一行对应的数字序列字符串，哈希表中记录有这个数字序列字符串的个数就是对应的行列对个数。

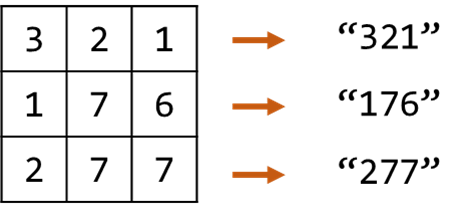
如果直接把数字进行拼接会造成歧义，可能不同的数字会有相同数字序列字符串。因此每一个数字之后添加一个标识符%进行区分。

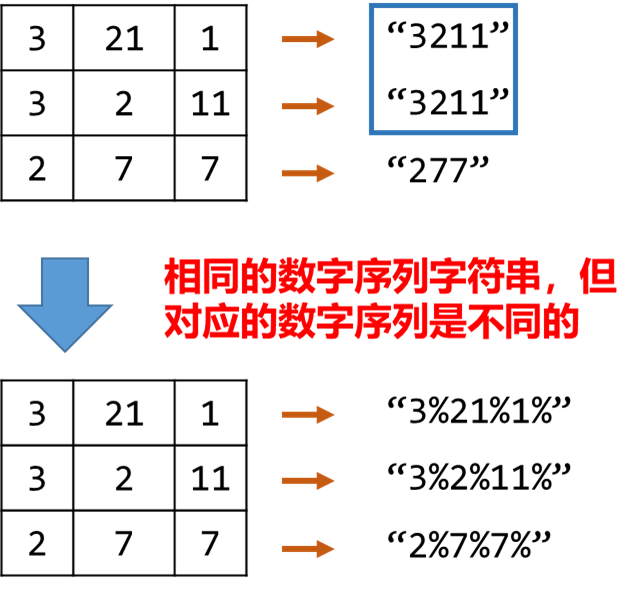
图解

以示例2进行图解

三、代码

3.1 三层循环

Java版本：

class Solution {public int equalPairs(int[][] grid) {int n = grid.length;int ans = 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {int ok = 1;for (int k = 0; k < n; ++k) {if (grid[i][k] != grid[k][j]) {ok = 0;break;}}ans += ok;}}return ans;}
}

C++版本：

class Solution {
public:int equalPairs(vector<vector<int>>& grid) {int n = grid.size();int ans = 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {int ok = 1;for (int k = 0; k < n; ++k) {if (grid[i][k] != grid[k][j]) {ok = 0;break;}}ans += ok;}}return ans;}
};

Python版本：

class Solution:def equalPairs(self, grid: List[List[int]]) -> int:g = [list(col) for col in zip(*grid)]return sum(row == col for row in grid for col in g)

3.2 哈希 + 二层循环

Java版本：

class Solution {public int equalPairs(int[][] grid) {int n = grid.length;    // 矩阵尺寸Map<String, Integer> rowSeqCount = new HashMap<>();     // 存储行数字序列字符串的哈希表StringBuilder sb ;      // 用于生成数字序列字符串String rowSeq;          // 数字序列字符串for(int i = 0; i < n; i++){     // 遍历每一行sb = new StringBuilder();   // 每一行新建一个对象// 生成行数字序列字符串for(int j = 0; j < n; j++){sb.append(grid[i][j]);sb.append('%');}rowSeq = sb.toString(); // 哈希表记录这个数字序列字符串个数rowSeqCount.put(rowSeq, rowSeqCount.getOrDefault(rowSeq, 0) + 1);}int count = 0;for(int j = 0; j < n; j++){     // 遍历每一列sb = new StringBuilder();   // 每一列新建一个对象// 生成列数字序列字符串for(int i = 0; i < n; i++){sb.append(grid[i][j]);sb.append('%');}rowSeq = sb.toString();// 从哈希表中查询是和这个列数字序列字符串相同的行数字序列字符串的个数count += rowSeqCount.getOrDefault(rowSeq, 0);}return count; }
}

C++版本：

class Solution {
public:int equalPairs(std::vector<std::vector<int>>& grid) {int n = grid.size(); // 矩阵尺寸std::unordered_map<std::string, int> row_seq_count; // 存储行数字序列字符串的哈希表for (int i = 0; i < n; i++) { // 用于生成数字序列字符串std::string row_seq = ""; // 每一行新建一个字符串// 生成行数字序列字符串for (int j = 0; j < n; j++) {row_seq += std::to_string(grid[i][j]) + "%";}// 哈希表记录这个数字序列字符串个数row_seq_count[row_seq] = row_seq_count[row_seq] + 1;}int count = 0;for (int j = 0; j < n; j++) { // 遍历每一列std::string row_seq = ""; // 每一列新建一个对象// 生成列数字序列字符串for (int i = 0; i < n; i++) {row_seq += std::to_string(grid[i][j]) + "%";}// 从哈希表中查询是和这个列数字序列字符串相同的行数字序列字符串的个数count += row_seq_count[row_seq];}return count;}
};

Python版本：

class Solution:def equalPairs(self, grid: List[List[int]]) -> int:n = len(grid)       # 矩阵尺寸row_seq_count = {}  # 存储行数字序列字符串的哈希表for i in range(n):  # 用于生成数字序列字符串row_seq = ""    # 每一行新建一个字符串# 生成行数字序列字符串for j in range(n):  row_seq += f"{grid[i][j]}%"# 哈希表记录这个数字序列字符串个数row_seq_count[row_seq] = row_seq_count.get(row_seq, 0) + 1count = 0for j in range(n):  # 遍历每一列row_seq = ""    # 每一列新建一个对象# 生成列数字序列字符串for i in range(n):row_seq += f"{grid[i][j]}%"# 从哈希表中查询是和这个列数字序列字符串相同的行数字序列字符串的个数count += row_seq_count.get(row_seq, 0)return count