1. 度量学习

现有的大部分算法对图像进行特征提取后化为向量的表达形式，其本质是把每一幅用于训练的图像

通过某种映射到欧氏空间的一个点，并利用欧氏空间的良好性质在其中进行学习器的训练。但定义

图像特征之间的欧氏距离未必能很好反映出样本之间的相似。通过训练样本寻找一种能够合理描述

当前样本相似度的距离度量，能够大大提高学习器的性能。  度量学习是机器学习的一个重要分

支，通过有标记样本或结合未标记样本，寻找一个能够在给定指标下最恰当刻画样本相似度的距离

矩阵或距离函数。

度量学习包括监督度量学习和半监督度量学习。监督度量学习主要是利用标注样本学习一个反映样

本语义关系的度量函数，使语义上相近的样本之间距离较近，反之则较远。 半监督度量学习则是

利用了标注样本，也利用了未标注样本。

1.1 监督度量学习

利用携带标注信息的训练数据进行距离度量学习，能更好的降低“语义鸿沟”的影响。 监督的距离度

量学习的主要思想是，利用标注数据学习一个度量矩阵，对样本进行映射变换，使得在变换后的度

量空间中，同类样本之间的距离变小，异类样本之间的距离变大，或使得相似的样本距离变小，不

相似的样本距离变大。可以通过设定不同的标注信息，使得距离度量结果符合不同的相似度评判标

准，因此度量方式的选择更加自由。

（1）基于凸规划的全局距离度量学习方法：该方法学习一个度量矩阵，使非相似样本间距离的平

方和最大，同时使相似样本间距离的平方和小于一定值。

（2）近邻成分分析：以概率的方式定义点的软邻域，然后通过最大化训练样本的留一法分类错误

率学习距离度量矩阵。该方法在训练度量矩阵的同时，保持了相邻数据点之间关系，但不一定能全

局最优。

（3）区分性成分分析：通过学习一种最优的数据转换使不同“团簇”间的方差和最大，所有“团簇”

内的方差和最小。

（4）基于信息论的距离度量学习方法：在满足约束信息的同时，使学习到的度量矩阵M和根据某

种先验知识给出的度量矩阵M0之间的 KL 散度最小。

（5）最大边界近邻分类：分类方法是将样本的 K 最近邻保持在同一类别中，同时使异类样本之间

的边界最大。其损失函数的第一项是惩罚输入样本和其最近邻间的距离，第二项是惩罚异类样本间

较小的距离。

1.2 半监督度量学习

监督度量学习只利用了有限的标注数据，且常会遇到训练数据不足的问题，而实际中却有大量未标

注的数据存在。半监督度量学习通过对未标注数据加以利用，以获得更准确的模型。

（1）07年，一种基于核的半监督距离度量学习方法

（2）09年，通过保留类似于 LLE局部线性嵌嵌入的局部关系学习距离度量

（3）Laplacian 正则化距离度量学习（LRML），将样本点的近邻看作相似点，联合已有标注数据

学习距离度量。

近年来，距离度量学习已成为智能信息处理方面的一个研究热点，研究表明，距离度量学习能够大

大提升了图像分类、图像匹配、及图像检索等工作的性能。

2. 降维

降维的动机：原始观察空间中的样本具有极大的信息冗余；样本的高维数引发分类器设计的“维数

灾难”；数据可视化、特征提取、分类与聚类等任务需求。

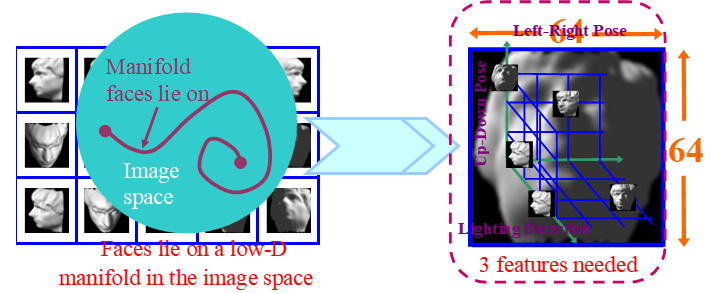
解决办法：选取尽可能多的, 可能有用的特征，然后根据需要进行特征/维数约简。 

实验数据分析，数据可视化（通常为2维或3维）等也需要维数约简。 

线性降维：通过特征的线性组合来降维，本质上是把数据投影到低维线性子空间，线性方法相对比

较简单且容易计算。代表方法：主成分分析(PCA)，线性判别分析(LDA)，多维尺度变换(MDS) 。

2.1 线性判别分析(LDA)

降维目的：寻找最能把两类样本分开的投影直线，使投影后两类样本的均值之差与投影样本的总类

散度的比值最大。求解方法：经过推导把原问题转化为关于样本集总类内散度矩阵和总类间散度矩

阵的广义特征值问题。

2.2 主成分分析(PCA)

主成分分析（Principal Component Analysis，简称PCA）是最常用的一种降维方法。对于正交属

性空间中的样本点，如何用一个超平面（直线的高维推广）对所有的样本进行恰当的表达？应该具

有两个性质：最近重构性：样本点到这个超平面的距离足够近最大可分性：样本点在这个超平面上

的投影能尽可能分开。

降维目的：寻找能够保持采样数据方差的最佳投影子空间，求解方法：对样本的散度矩阵进行特征

值分解，所求子空间为经过样本均值，以最大特征值所对应的特征向量为方向的子空间。

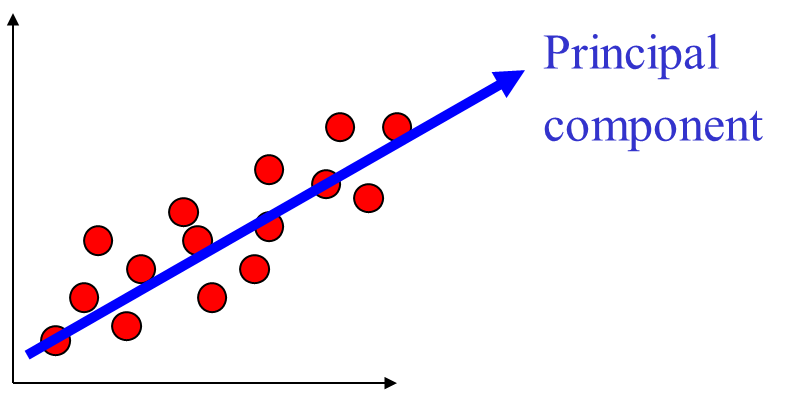
PCA对于椭球状分布的样本集有很好的效果，学习所得的主方向就是椭球的主轴方向。PCA 是一

种非监督的算法，能找到很好地代表所有样本的方向，但这个方向对于分类未必是最有利的。

考虑最近重构性和最大可分性两个优化目标，得到如下推导：

假定数据样本进行了中心化，即；再假定投影变换后得到的新坐标系为

其中wi是标准正交基向量，。若丢弃新坐标系中部分坐标，即将维

度降低到d'<d，则样本点xi在低维坐标系中的投影是，其中；是

xi在低维坐标系下第j维的坐标，若基于zi来重构xi，则会得到。

考虑整个训练集，原样本点与基于投影重构的样本点之间的距离为：

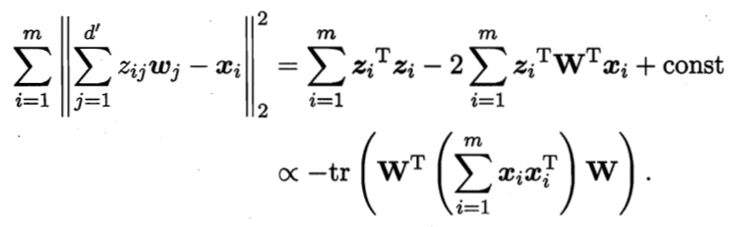
根据最近重构性，上式应被最小化，考虑到wj是标准正交基，是协方差矩阵，有

这就是主成分分析的优化目标。

从最大可分性出发，能得到主成分分析的另一种解释，我们知道，样本点xi在新空间中超平面上的

投影是，若所有样本点的投影能尽可能分开，则应该使投影后样本点的方差最大化，如下

图所示。

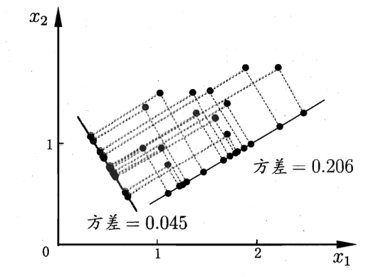
使所有样本的投影尽可能分开，则需最大化投影点的方差。

投影后样本点的方差是，于是优化目标可写为

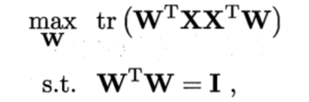
 对上式使用拉格朗日乘子法可得。

于是，只需对协方差矩阵xxT进行特征值分解，将求得的特征值排序：，再取

前d'个特征值对应特征向量构成。这就是主成分分析的解。PCA算法描述：

降维后低维空间的维数d通常是由用户事先指定，或通过在d值不同的低维空间中对k近邻分类器

（或其他开销较小的学习器）进行交叉验证来选取较好的d值.对PCA，还可从重构的角度设置一个重构阈值，例如t=95%，然后选取使下式成立的最小 d' 值：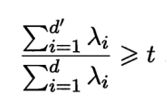 

PCA 仅需保留 W 与样本的均值向量即可通过简单的向量减法和矩阵—向量乘法将新样本投影至低

维空间中，显然，低维空间与原始高维空间必有不同，因为对应于最小的d—d'个特征值的特征向

量被舍弃了，这是降维导致的结果。但舍弃这部分信息往往是必要的：一方面，舍弃这部分信息之

后能使样本的采样密度增大，这正是降维的重要动机；另一方面，当数据受到噪声影响时，最小的

特征值所对应的特征向量往往与噪声有关，将它们舍弃能在一定程度上起到去噪的效果。

def pca(dataMat,topNfeat=9999999):   meanVals=mean(dataMat,axis=0)    	meanRemoved=dataMat-meanVals # 去除平均值    covMat=cov(meanRemoved,rowvar=0)    	eigVals,eigVects=linalg.eig(mat(covMat))    	eigValInd=argsort(eigVals)    # 从大到小对N个值排序    	eigValInd=eigValInd[:-(topNfeat+1):-1]    	redEigVects=eigVects[:,eigValInd]    # 将数据转换到新空间    	lowDDataMat=meanRemoved*redEigVects    	reconMat=(lowDDataMat*redEigVects.T)+meanVals    return lowDDataMat,reconMat

2.3  多维缩放(MDS) 

MDS 是一种非监督的维数约简方法。MDS的基本思想：约简后低维空间中任意两点间的距离。应

该与它们在原高维空间中的距离相同。MDS的求解：通过适当定义准则函数来体现在低维空间中

对高维距离的重建误差，对准则函数用梯度下降法求解。对于某些特殊距离可以推导出解析解法。

若要求原始空间中样本之间的距离在低维空间中得以保持，即多维缩放（Multiple Dimensional

Scaling,MDS）。

假定m个样本在原始空间的距离矩阵为𝐷∈𝑅^(𝑚×𝑚)，其第i行j列的元素𝑑𝑖𝑠𝑡𝑖𝑗为样本 𝑥𝑖 到 𝑥𝑗 的距

离。我们的目标是获得样本在𝑑′维空间的表示𝐷∈𝑅^(𝑑′×𝑚)，𝑑′≤𝑑，且任意两个样本在𝑑′维空间中的

欧式距离等于原始空间中的距离，即。 

令，其中B为降维后样本的内积矩阵，，有：

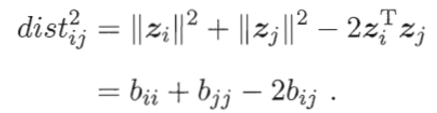
为便于讨论，令降维后的样本Z被中心化，即。显然，矩阵B的行与列之和均为零，即

。易知：

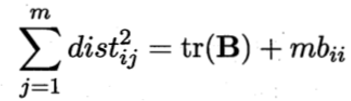
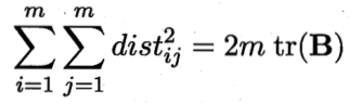
其中tr(·)表示矩阵的迹(trace)，tr(B)=令：

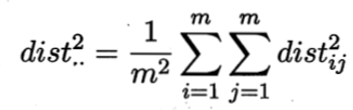
由上式可得：

由此即可通过降维前后保持不变的距离矩阵D求取内积矩阵B。

对矩阵B做特征值分解(eigenvalue decomposition))，，其中

为特征值构成的对角矩阵，，V为特征向量矩阵。假定其中有d*个非零特

征值，它们构成对角矩阵，令V*表示相应的特征向量矩阵，则Z可表达

为。

在现实应用中为了有效降维，往往仅需降维后的距离与原始空间中的距离尽可能接近，而不必严格

相等。此时可取d`<<d个最大特征值构成对角矩阵，令V表示相应的特征

向量矩阵，则Z可表达为。

算法描述：

MDS降维步骤：

①保持原始空间样本之间的距离和低维空间中的距离相等。这是MDS降维方法的前提和条件，但

是在实际的应用中，在本文后面的分析中会发现，我们并不会保证样本之间距离在降维前后保持百

分之百不变，而是使得降维前后样本距离大致一致。

②对原始数据进行归一化后，保证所有属性的数据点全部落在[0,1]区间内，这样方便后面MDS算

法处理。

③使用两层for循环，对原始数据样本分别进行行和列遍历，最后得m个样本在原始空间的距离矩阵

𝐷∈𝑅^(𝑚×𝑚)，现在我们的目标是获得样本在d’维空间中的表示𝐷∈𝑅^(𝑑′×𝑚)，其中d’<=d，并且两

个样本在d’维空间中的欧氏距离等于原始空间中的距离。

④首先构造矩阵，其中Z表示的是降维后的样本矩阵。经过一系列的推导过程，

最后能够得到如下的计算公式：，根据这个公式，我们就

能够计算出矩阵B中每一个元素的值。

⑤对矩阵B做特征值分解，其中是特征值构成的对角矩阵，满

足，V表示特征向量矩阵。如果特征值中有 𝑑∗个非零特征值，那么我们将

得到如下计算Z矩阵的表达式：                            

在该式中，矩阵Z的每一列表示一个样本，每一行表示降维后在d’空间内的一个维度，由于d’<=d,

因此也就达到了降维的目的。后续的分析中，我们只需要修改d’的值，就可以将原数据样本降维到

我们想要的维度了。