画家问题
题目描述
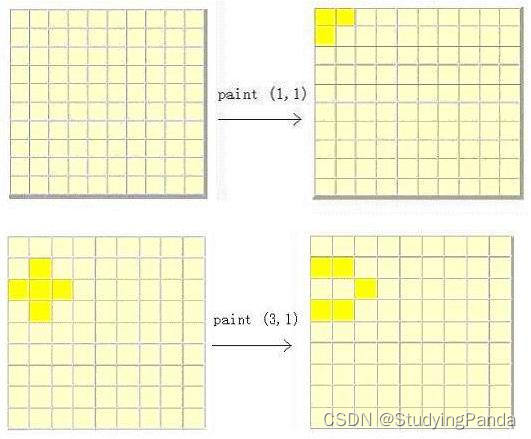
有一个正方形的墙,由N*N个正方形的砖组成,其中一些砖是白色的,另外一些砖是黄色的。Bob是个画家,想把全部的砖都涂成黄色。但他的画笔不好使。当他用画笔涂画第(i, j)个位置的砖时, 位置(i-1, j)、 (i+1, j)、 (i, j-1)、 (i, j+1)上的砖都会改变颜色。请你帮助Bob计算出最少需要涂画多少块砖,才能使所有砖的颜色都变成黄色。
关于输入
第一行是个整数t(1≤t ≤20),表示要测试的案例数。然后是t个案例。每个案例的首行是一个整数n (1≤n ≤15),表示墙的大小。接下来的n行表示墙的初始状态。每一行包含n个字符。第i行的第j个字符表示位于位置(i,j)上的砖的颜色。“w”表示白砖,“y”表示黄砖。
关于输出
每个案例输出一行。如果Bob能够将所有的砖都涂成黄色,则输出最少需要涂画的砖数,否则输出“inf”。
例子输入
2 3 yyy yyy yyy 5 wwwww wwwww wwwww wwwww wwwww
例子输出
0 15
解题分析
要解决这个问题,我们先去思考一下,怎么涂才能把全部区块涂满呢?又有多少种的解法?显然,我们没有办法直接一眼就看出来怎么去涂,并且题目也要求我们去求一个最少的操作步骤,所以枚举是不可避免的,关键是我们如何去枚举呢?
其实我们一行一行地涂,考虑第一行每一个区块是否涂就可以了,后面的每一行都是根据前一行的状态去确定是否填涂的,如果前一行中有白色的砖块,那么它的下一行的这个砖块必然要涂,否则不可能把全部砖块都涂满,这样的话问题就清晰起来了,其实我们只要去枚举第一行的全部情况即可,每个方块只有涂和不涂两种状态,所以说,最多也就2的15次方种情况,这是一个可以接受的数字。
最后只要检查最后一行有没有被涂满就行了。
- 首先,我们定义一个递归函数draw,用于将指定位置的砖及其周围砖的颜色进行反转。具体操作是,如果砖是白色的,则改为黄色,反之亦然。同时,将周围砖的颜色也进行反转。
- 然后,我们定义一个递归函数print,用于检查当前墙的状态是否可以全部涂成黄色。具体操作是,从上到下每一行进行遍历:
- 如果是第一行,则遍历每一列,将该位置及其周围砖的颜色进行反转,并设置count数组的相应位置为1(表示已经涂过颜色)。
- 如果是其他行,则遍历上一行中颜色为白色的位置,在该位置上进行反转,并设置count数组的相应位置为1(表示已经涂过颜色)。
- 递归调用print函数,进行下一行的涂色操作。
- 在每一行结束时,检查最后一行是否所有砖都变为黄色,如果是,则计算涂色的砖数ans,并将ans与当前最小涂色砖数ANS进行比较,取较小值。
- 接下来,我们定义一个递归函数fill,用于枚举第一行中的每个位置是否涂色。具体操作是,对于每个位置,递归调用fill函数,分别设置该位置涂色和不涂色,并进行下一行的涂色操作。
- 在主函数中,读入测试案例的数量t,并进行t次测试。对于每个测试案例,读入墙的大小n和初始状态的墙面颜色。初始化一个标记数组is,用于记录第一行中每个位置是否涂色。初始化最小涂色砖数ANS为无穷大。
- 调用fill函数,开始进行所有位置的枚举涂色操作。在fill函数中,递归调用fill函数,对第一行中的每个位置进行设置涂色和不涂色。在每个位置上进行设置涂色或不涂色后,调用print函数,进行下一行的涂色操作。
- 在print函数中,检查是否最后一行的所有砖都变为黄色。如果是,则计算涂色的砖数ans,并将ans与当前最小涂色砖数ANS进行比较,取较小值。
- 在主函数中,将最小涂色砖数ANS输出。如果ANS为无穷大,则输出"inf"。
代码实现
#include <iostream>
#include <cstring>
using namespace std;int t=0,n=0,ANS=1e9;;
char board1[16][16],board2[16][16];
const int dx[]={-1,1,0,0};
const int dy[]={0,0,-1,1};
bool is[16]={0}, count[16][16];void draw(int x,int y){if(board2[x][y]=='w') board2[x][y]='y';else board2[x][y]='w';for(int i=0;i<4;i++){int nx=x+dx[i],ny=y+dy[i];if(nx>=1 && nx<=n && ny>=1 && ny<=n){if(board2[nx][ny]=='w') board2[nx][ny]='y';else board2[nx][ny]='w';}}
}void print(int row){if(row==n+1){for(int i=1;i<=n;i++){if(board2[n][i]=='w'){return;}}int ans=0;for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){if(count[i][j]) ans++;}ANS=min(ANS,ans);return;}if(row==1){for(int i=1;i<=n;i++){if(is[i]){draw(row,i);count[row][i]=1;}}print(row+1);}else{for(int i=1;i<=n;i++){if(board2[row-1][i]=='w'){draw(row,i);count[row][i]=1;}}print(row+1);}
}void fill(int step){if(step==n+1){memcpy(board2,board1,sizeof(board1));memset(count,0,sizeof(count));print(1);return;}for(int i=0;i<2;i++){if(i==0){is[step]=1;fill(step+1);}else{is[step]=0;fill(step+1);}}
}int main(){scanf("%d",&t);while(t--){scanf("%d",&n);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){scanf(" %c",&board1[i][j]);}}memset(is,0,sizeof(is));ANS=1e9;fill(1);if(ANS!=1e9)printf("%d\n",ANS);elseprintf("inf\n");}return 0;
}













)


)
)
