文章目录
- 前言
- 什么是位运算算法
- 1.判断字符是否唯一
- 1.1 题目要求
- 1.2 做题思路
- 1.3 Java代码实现
- 2. 丢失的数字
- 2.1 题目要求
- 2.2 做题思路
- 2.3 Java代码实现
- 3. 两数之和
- 3.1 题目要求
- 3.2 做题思路
- 3.3 Java代码实现
- 4. 只出现一次的数字
- 4.1 题目要求
- 4.2 做题思路
- 4.3 Java代码实现
- 5. 消失的两个数字
- 5.1 题目要求
- 5.2 做题思路
- 5.3 Java代码实现
- 总结
前言
位操作符想必大家都知道吧,&——按位与,|——按位或,^——按位异或,~——按位取法,位操作主要是用来操作二进制数的,就是因为它操作的是二进制,所以它的速度非常的快,那么既然他的速度很快,我们是否可以用位运算来解决一些实际问题呢?当然是可以的,这篇文章我将为大家分享如何使用位运算这种算法来解决一些问题。
什么是位运算算法
位运算算法是一组基于二进制位的操作符和操作方法的算法,用于在计算机中对二进制数字进行快速和高效的操作。位运算算法可以在二进制位级别上进行操作,包括位与(AND)、位或(OR)、位异或(XOR)、位取反(NOT)以及移位操作(左移和右移)等。
- 按位与(&):只有当两个比特位都为1的时候结果才为1,否则为0
- 按位或(|):两个比特位中有一个1,结果就为1
- 按位异或(^):两个比特位相同为0,相异为1
- 按位取反(~):除符号位之外,其它的比特位取反,为0结果为1,为1结果为0
位运算算法常用于以下情况:
- 位操作:可以通过位与、位或、位异或等运算符来对二进制数字的每一位进行操作,实现快速的位级别操作。
- 位掩码:可以使用位运算来创建和操作掩码,掩码经常用于标志位、权限控制和位字段的操作。
- 整数运算优化:位运算算法可以实现某些整数运算的高效实现,如乘以2的幂次方、除以2的幂次方、判断奇偶性等。
- 位图算法:位运算常用于位图算法,其中每个二进制位表示集合中的一个元素,可以进行高效的集合操作,如并集、交集、差集等。
- 压缩算法:位运算可以在压缩算法中起到重要的作用,用于压缩和解压缩数据,常见的例子包括哈夫曼编码和算术编码。
位运算算法通常具有高效性、简洁性和可移植性的特点,可以提供快速的底层操作,特别适合某些特定的问题和应用领域。在编写低级别的系统程序、嵌入式系统、网络协议和算法优化等方面,位运算算法发挥着重要的作用。
1.判断字符是否唯一
https://leetcode.cn/problems/is-unique-lcci/
1.1 题目要求
实现一个算法,确定一个字符串 s 的所有字符是否全都不同。
示例 1:
输入: s = "leetcode"
输出: false
示例 2:
输入: s = "abc"
输出: true
限制:
- 0 <= len(s) <= 100
- s[i]仅包含小写字母
- 如果你不使用额外的数据结构,会很加分。
class Solution {public boolean isUnique(String astr) {}
}
1.2 做题思路
通常判断唯一性的时候,我们首先想到的是哈希表,但是这里限制我们不适用额外的数据结构,我们虽然可以使用数组来模拟哈希表,但这都不是最优解,这道题最优的解法就是使用位图的思想。为什么会选择使用位图呢?因为题目中说明了:字符串中只包含小写字母,也就是无重复字符的字符串的长度最长为26,而一个整型0有4个字节,32个比特位,并且二进制的0和1则恰好可以标志某一字符有或者没有。
那么如何使用位图的思想来解决这个问题呢?我们可以将每一个字符所代表的ASCII码值来表示它在32个比特位中的位置,用循环来遍历字符串中的每一个字符,如果该字符在32个比特位中的对应位置是0的话,则用 | 运算,将该位置变为1,如果该位置为 1 的话,则说明出现了重复的字符。
1.3 Java代码实现
class Solution {public boolean isUnique(String astr) {//鸽巢原理,当字符串长度大于26的时候一定会有重复的字符if(astr.length() > 26) return fasle; int tmp = 0; //tmp 代表32位比特位的位图for(int i = 0; i < astr.length(); i++) {char ch = astr.charAt(i);if(((tmp >> (ch - 'a')) & 1) == 1) return false;else tmp = tmp | (1 << (ch - 'a'));}return true;}
}
2. 丢失的数字
https://leetcode.cn/problems/missing-number/
2.1 题目要求
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
示例 1:
输入:nums = [3,0,1]
输出:2
解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,
因为它没有出现在 nums 中。
示例 2:
输入:nums = [0,1]
输出:2
解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,
因为它没有出现在 nums 中。
示例 3:
输入:nums = [9,6,4,2,3,5,7,0,1]
输出:8
解释:n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,
因为它没有出现在 nums 中。
示例 4:
输入:nums = [0]
输出:1
解释:n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,
因为它没有出现在 nums 中。
提示:
- n == nums.length
- 1 <= n <= 104
- 0 <= nums[i] <= n
- nums 中的所有数字都 独一无二
class Solution {public int missingNumber(int[] nums) {}
}
2.2 做题思路
这道题目的意思就是,原本数组中的元素应该是[0,数组长度],但是数组中缺少了一个数字,我们需要找到这个缺失的数字。这个题有很多种解法:
- 哈希表。
- 高斯求和。将原本数组中的元素的和减去现有数组所有元素的和就得到缺失的那个数字
- 排序。将数组进行排序,然后遍历数组找到缺失的那个数字
- 位运算
能用位运算解决就尽量用位运算来解决,因为位运算的速度非常快,那么这道题如何使用位运算来解决呢?在这之前,我们需要知道,^ 操作,当两个相同的数字进行异或操作的时候结果为0,那么我们可以将原本数组中元素和现有数组中的元素都进行异或操作,相同的两个数异或结果为0,到最后异或的结果就是我们要找的那个缺失的数字。
2.3 Java代码实现
class Solution {public int missingNumber(int[] nums) {int ret = 0;for(int n : nums) ret ^= n;for(int i = 0; i <= nums.length; i++) ret ^= i;return ret;}
}
3. 两数之和
https://leetcode.cn/problems/sum-of-two-integers/
3.1 题目要求
给你两个整数 a 和 b ,不使用 运算符 + 和 - ,计算并返回两整数之和。
示例 1:
输入:a = 1, b = 2
输出:3
示例 2:
输入:a = 2, b = 3
输出:5
提示:
- -1000 <= a, b <= 1000
class Solution {public int getSum(int a, int b) {}
}
3.2 做题思路
两数之和,大家一看到这个题目可能就会觉得很简单,直接 return a + b; 不就行了吗?但是仔细看题目,这道题不允许使用运算符 + 和 -,那么如何在不使用运算符的情况下实现两数之和呢?位运算,通过位运算就可以在不适用运算符的情况下实现两数之和的运算。
当我们进行二进制的加法的时候,当两个比特位相加的结果为2的时候,就需要向前进一位,但是我们可以先使用 ^ 操作来进行无进位的加法,当两个比特位相加的结果为2时,不进行进位而得到的结果,然后再使用 & 操作,来得到什么时候该进位,然后将 & 的结果向左移动一位,将上面的两个结果再循环进行上面的操作,直到 & 得到的结果为0的时候,就得到了两数之和的结果。

3.3 Java代码实现
class Solution {public int getSum(int a, int b) {while(b != 0) {int x = a ^ b;int y = a & b;a = x;b = y << 1;}return a;}
}
4. 只出现一次的数字
https://leetcode.cn/problems/single-number-ii/
4.1 题目要求
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
示例 1:
输入:nums = [2,2,3,2]
输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99]
输出:99
提示:
- 1 <= nums.length <= 3 * 104
- -231 <= nums[i] <= 231 - 1
- nums 中,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次
class Solution {public int singleNumber(int[] nums) {}
}
4.2 做题思路
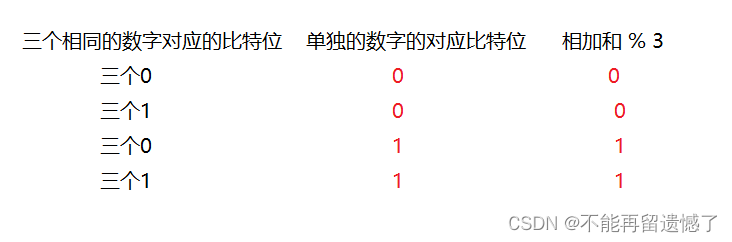
通过题目,我们可以知道,除了那个只出现了一次的数字之外,其他的数字都出现了一次,所以呢,我们可以将数组中的每个元素的32个比特位分别相加,将结果 % 3,就会得到那个只出现一次的数字的对应比特位。
4.3 Java代码实现
class Solution {public int singleNumber(int[] nums) {int ret = 0;for(int i = 0; i < 32; i++) {int tmp = 0;for(int n : nums) {tmp += (n >> i) & 1;}ret |= (tmp % 3) << i;}return ret;}
}
5. 消失的两个数字
https://leetcode.cn/problems/missing-two-lcci/
5.1 题目要求
给定一个数组,包含从 1 到 N 所有的整数,但其中缺了两个数字。你能在 O(N) 时间内只用 O(1) 的空间找到它们吗?
以任意顺序返回这两个数字均可。
示例 1:
输入: [1]
输出: [2,3]
示例 2:
输入: [2,3]
输出: [1,4]
提示:
- nums.length <= 30000
class Solution {public int[] missingTwo(int[] nums) {}
}
5.2 做题思路
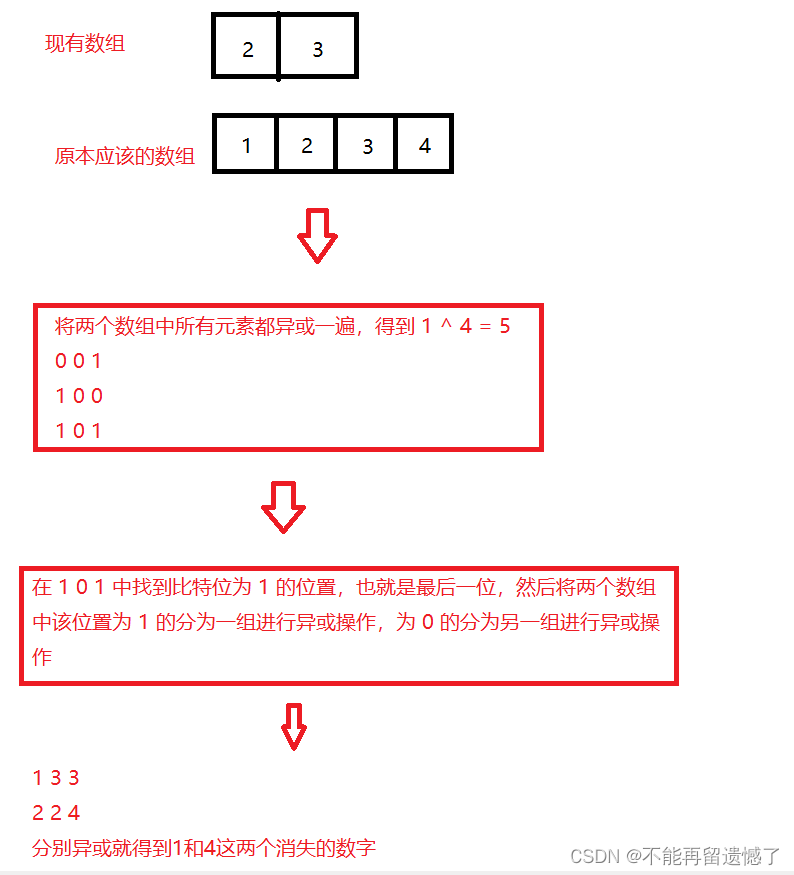
这个题目跟上面的消失的一个数字其实是类似的,只不过这里出现了两个消失的数字,我们不可能一次就找到两个消失的数字,但是我们可以分两次找。可以将这道题目转换为数组中只出现了一次的数字,这里大家可以看看我之前写过的一篇文章寻找单身狗,但是呢一个数组中只能找到一个只出现了一次的数字,如果要想找到两个只出现了一次的数字,我们可以将这两个消失的数组分别给分到两个不同的数组中,然后在每一个数组中找那个只出现了一次的数字,最终这两个消失的数字都会被找到。那么,如何将这两个消失的数字分在两个不同的数组中呢?同样是将原本的数组和现有的数组中的所有元素都进行异或操作,相同的元素异或为0,最后剩下的其实就是这两个消失的数字异或的结果,然后我们需要在这个异或的结果中找到比特位为 1 的位置,因为异或,相异为 1 ,相同为0,当找到这个为 1 的比特位之后,就可以将这些元素进行分组了,该比特位为 1 的为一组,为 0 的为另一组。
5.3 Java代码实现
class Solution {public int[] missingTwo(int[] nums) {int[] ret = new int[2];int tmp = 0;for(int n : nums) tmp ^= n;for(int i = 1; i <= nums.length + 2; i++) tmp ^= i;int flg = 0; //用来记录异或结果比特位为1的位置for(int i = 0; i < 32; i++) {if(((tmp >> i) & 1) == 1) {flg = i;break;}}for(int n : nums) {if(((n >> flg) & 1) == 1) ret[0] ^= n;else ret[1] ^= n;}for(int i = 1; i <= nums.length + 2; i++) {if(((i >> flg) & 1) == 1) ret[0] ^= i;else ret[1] ^= i;}return ret;}
}
总结
通过本篇博客,我们深入了解了位运算算法及其在计算机领域中的重要性和应用。位运算算法是一项强大的工具,它基于二进制位的操作,能够高效地处理二进制数据,提升程序的性能和效率。
在实际应用中,我们可以利用位运算算法来实现各种位级别的操作,如位掩码、位操作、整数运算优化、位图算法和压缩算法等。这些算法和技巧可以在底层系统编程、嵌入式系统、网络协议和算法优化等领域发挥重要作用。
然而,在使用位运算算法时,也需要注意一些优化技巧和注意事项。我们需要注意位运算的优先级、位移操作的性能和溢出问题,以及如何利用位运算进行快速乘法、除法和判断奇偶性等操作。深入理解这些技巧,能够更好地应用位运算算法,提高代码的效率和准确性。
位运算算法是计算机科学中一个广泛应用的领域,通过深入学习和实践,我们可以进一步探索和发现更多有趣的位运算技巧和应用。在日常编程中,合理运用位运算算法,能够帮助我们解决一些复杂的问题,实现更高效和可靠的程序。
希望本篇博客能够为读者提供一个全面而清晰的位运算算法入门指南,让大家对位运算算法有更深入的了解,并能够应用于实际开发中。通过不断学习和探索,我们可以进一步提升自己的编程能力,并在算法领域中取得更多的成就。
感谢您的阅读,希望本篇博客对您有所帮助。如果您有任何问题或反馈,欢迎留言交流。祝愿您在位运算算法的学习和应用中取得成功!




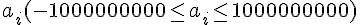






![[C/C++]天天酷跑游戏超详细教程-上篇](https://img-blog.csdnimg.cn/79e2f0cd769945f5b326f0c2dcb85c74.jpeg)