一、图的基本表示和特征工程

1.1 什么是图

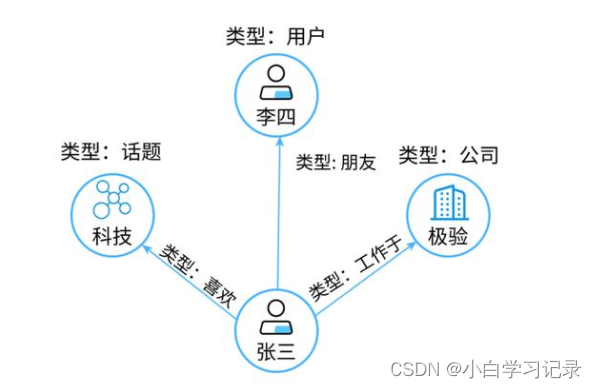
图是由节点和边组成的，如下图所示。一般图中的节点表示实体对象（比如一个用户、一件商品、一辆车、一张银行卡等都可以作为节点），边代表事件或者实体之间的特殊关系（比如用户和商品之间的购买关系）。

---

1.2 图的基本表示

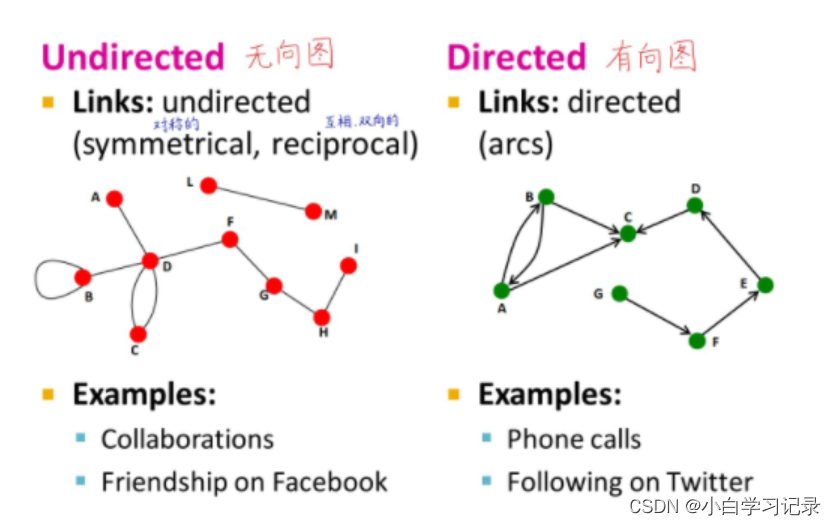
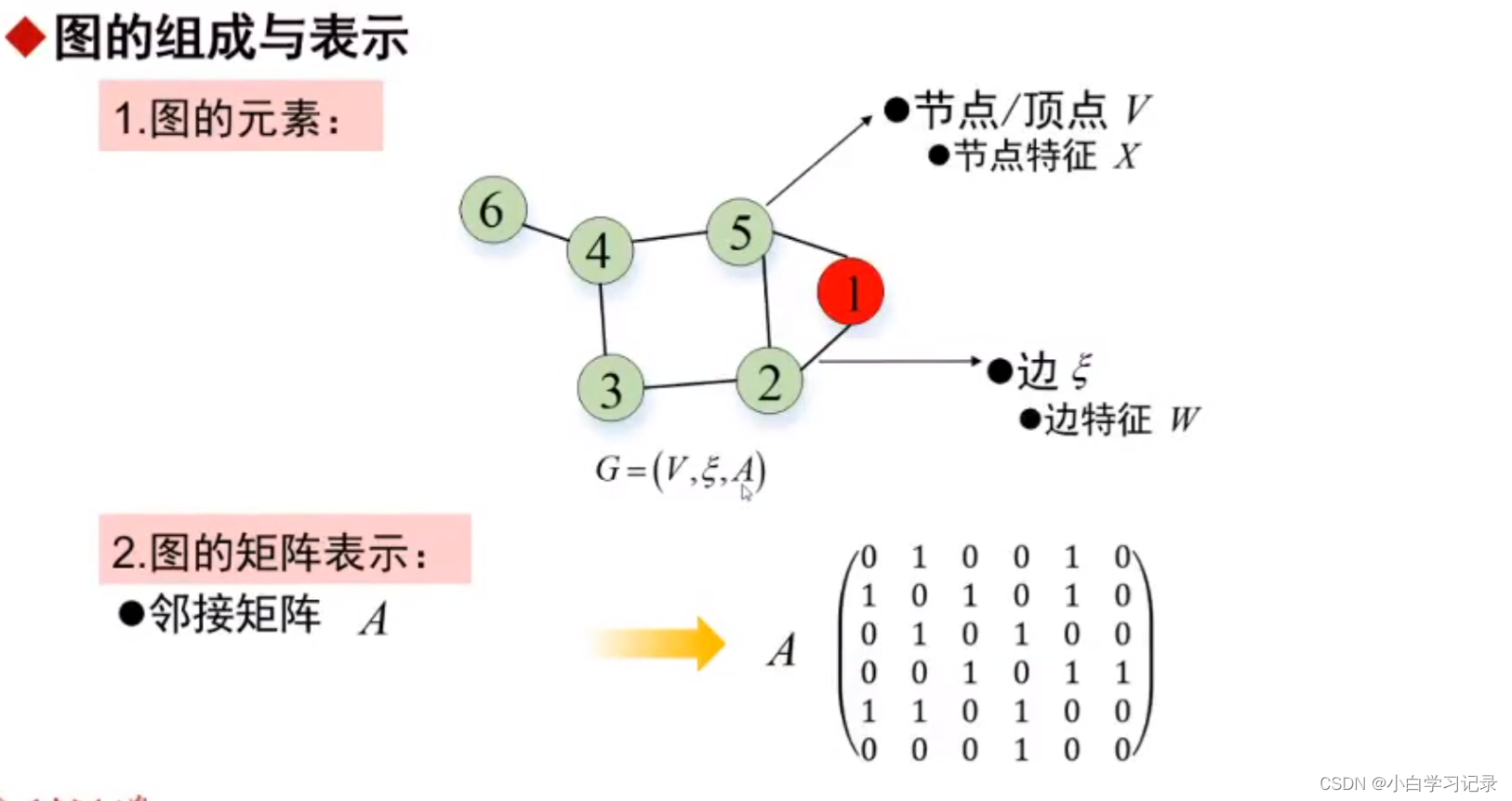
如何去表示一张图？

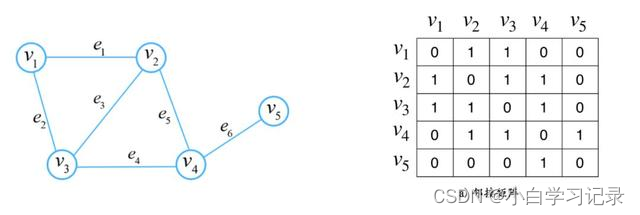
在数学中，我们一般使用邻接矩阵来表示图，如上图右边所示。邻接矩阵中的值为 1 表示节点之间有边，即有连接关系。所以邻接矩阵其实很好的将图的这种结构信息表达出来了。
此外，有的图网络比较庞大，故也采用连接列表和邻接列表来表示图。

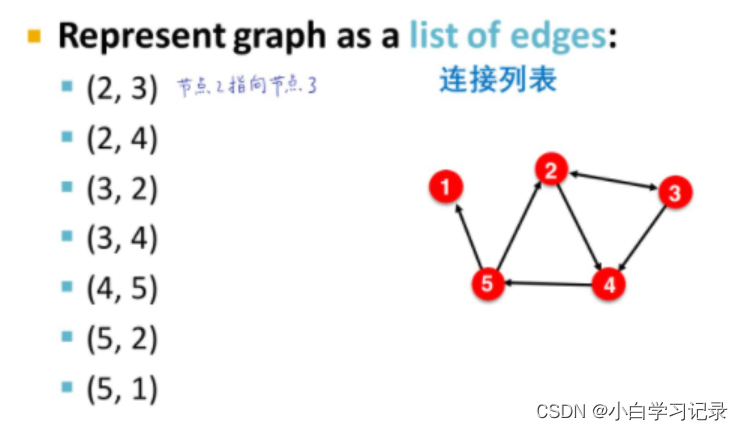
连接列表只记录存在连接的节点对

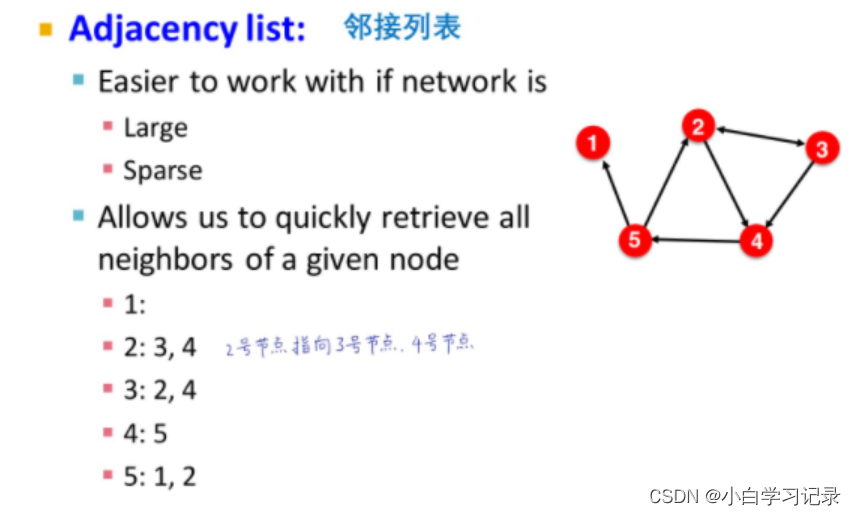
邻接列表只记录存在关系的节点对，每个节点依次排开，只记录与它有关系的节点

1.3 图的性质–度（degree)

---

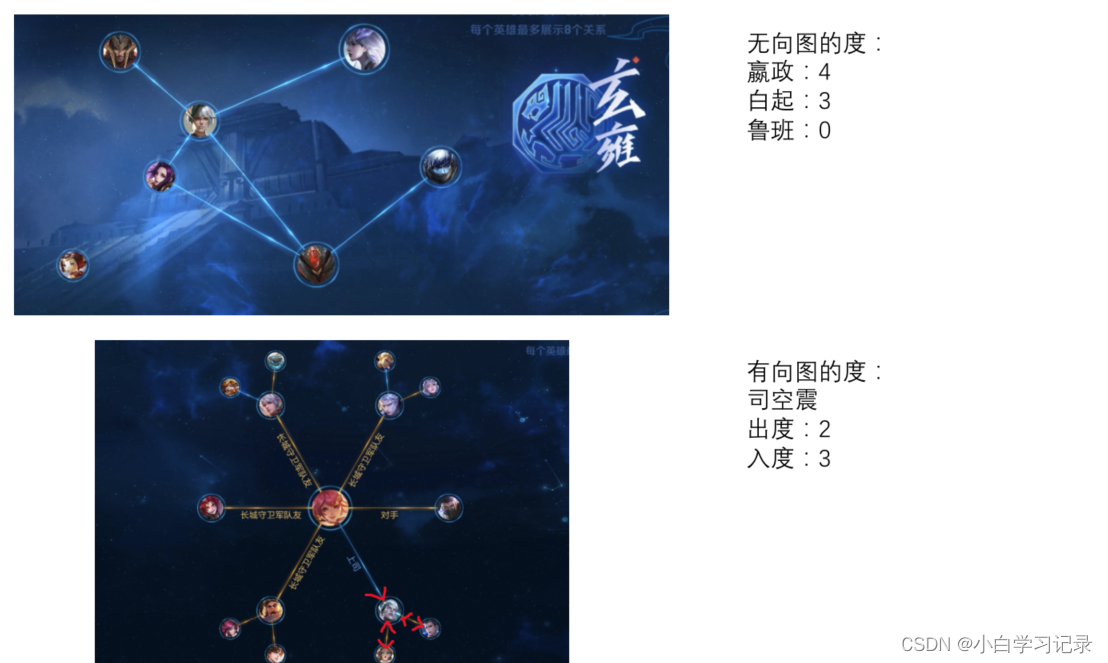
节点的度(Degree)表示与该节点相连的边的个数，记作d(v)。对于n个节点的简单图G=(V, E)，其度矩阵D为，也是一个对角矩阵。

---

1.4 连通图，连通分量

对于一个无向图，如果任意的节点i能够通过一些边到达节点j ，则称之为连通图

1.5有向图连通性

1.6图直径

图直径：两两节点中最长的最短路径

1.7度中心性

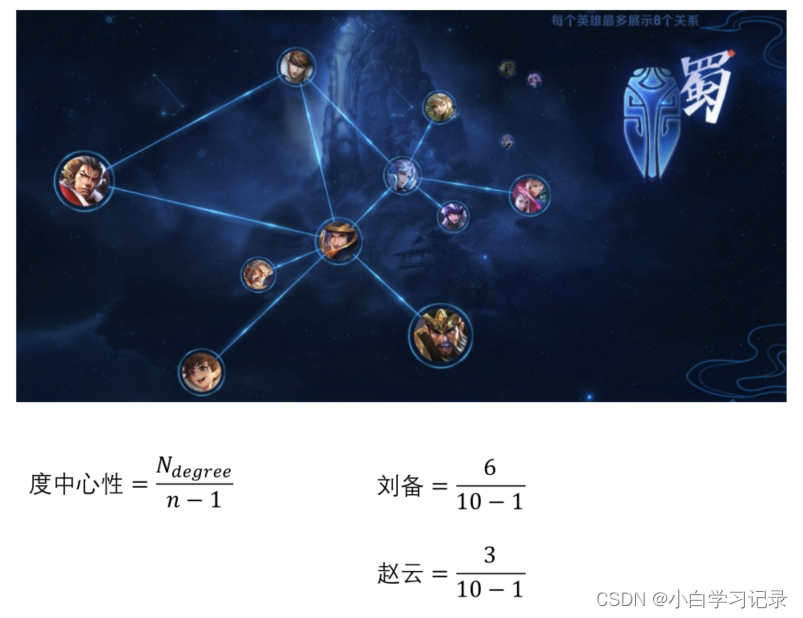
1.7特征中心性（ Eigenvector Centrality）

特征中心性：最大特征值对应的特征向量。

---

---

1.8中介中心性 Betweenness Centrality、

---

1.9连接中心性 Closeness

---

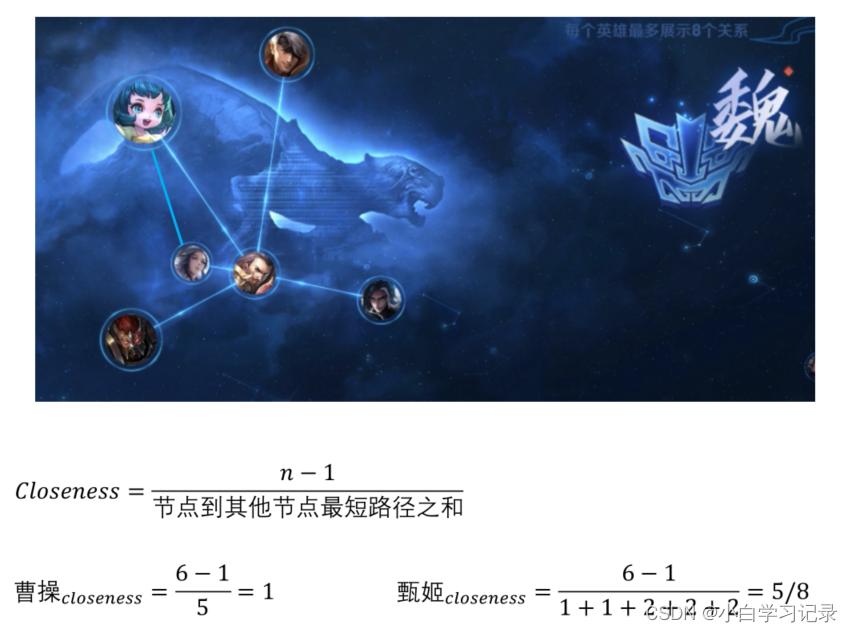
1.10PageRank

基本思路
一个页面很重要：如果他被其他重要的pages指向。

• 每个链接的投票与其源页面的重要性成正比
• 如果具有重要性的页面 i 具有 di 个连出链接，则每个链接都会获得 ri / di 投票
• 页面j本身的重要性rj是其连入链接的投票总和

rj 是节点j的importance score

1.10HITS

二、图神经网络

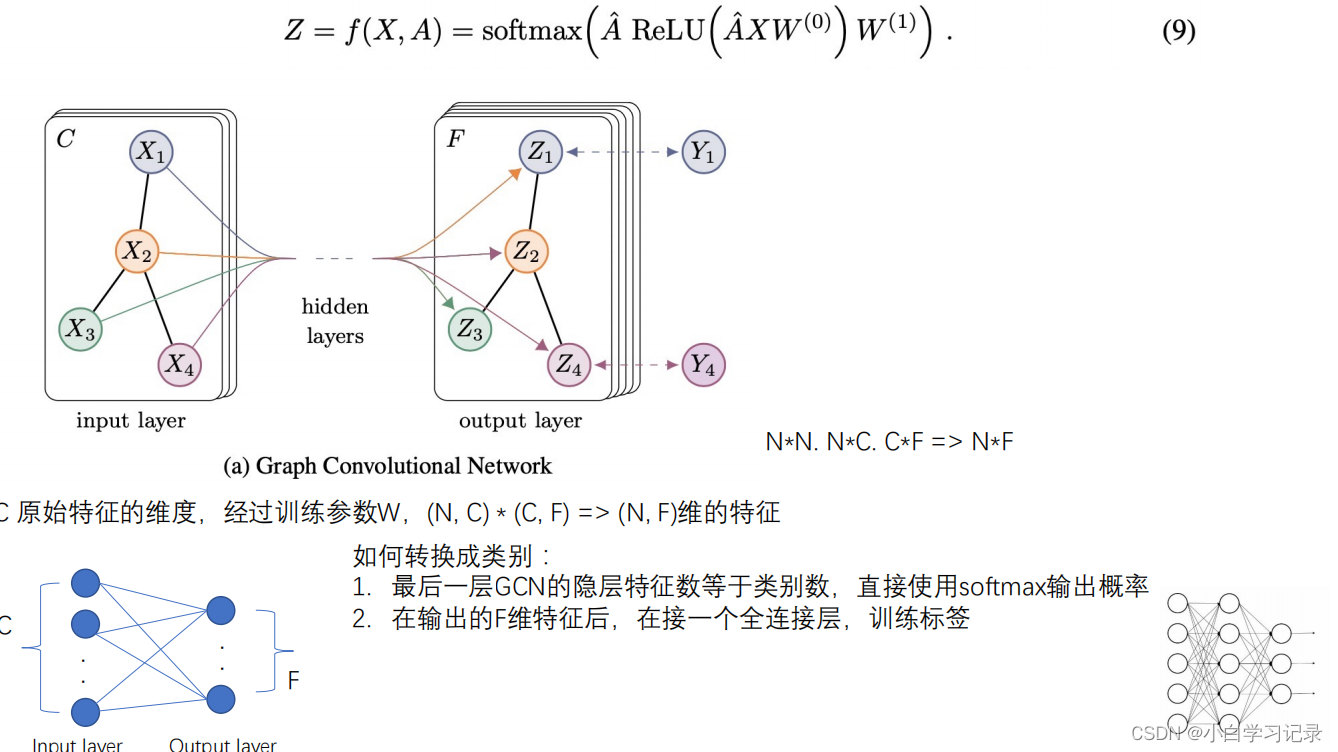
2.1GCN

整体示意图

---

---

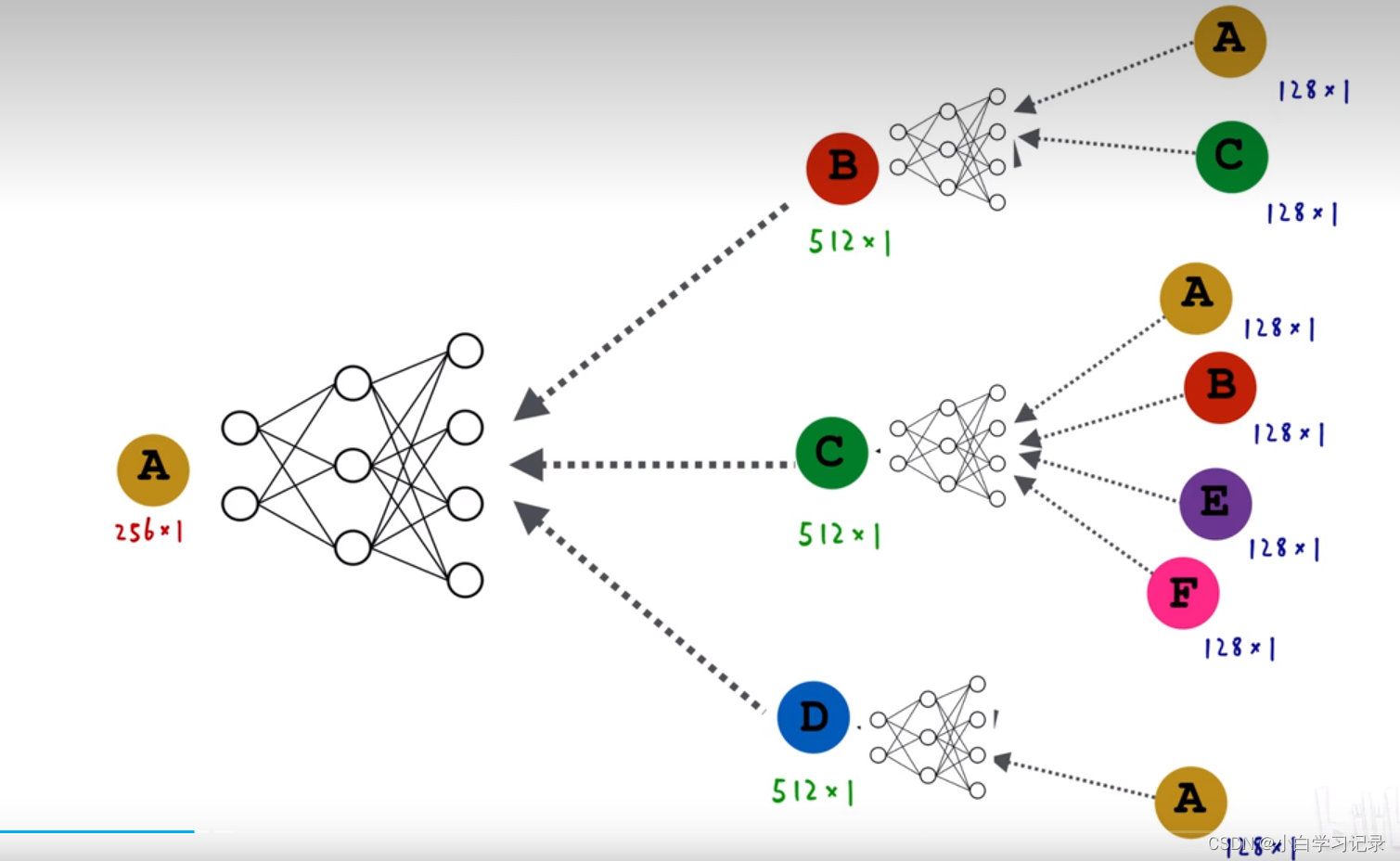
公式原理：

---