网址大全官网下载/站长工具seo综合查询推广

网址大全官网下载,站长工具seo综合查询推广,公司网站被黑有不良信息做笔录,楼盘价格哪个网站做的好【专栏】数据结构复习之路这篇文章来自上述专栏中的一篇文章的节选： 【数据结构复习之路】图（严蔚敏版）两万余字&超详细讲解想了解更多图论的知识，可以去看看本专栏 Dijkstra 算法讲解： 迪杰斯特拉算法(Di…

【专栏】数据结构复习之路

这篇文章来自上述专栏中的一篇文章的节选：

【数据结构复习之路】图（严蔚敏版）两万余字&超详细讲解

想了解更多图论的知识，可以去看看本专栏

Dijkstra 算法讲解：

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是：从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

这里我直接以书P189那个例子为基础进行讲解（附带书上的源代码）

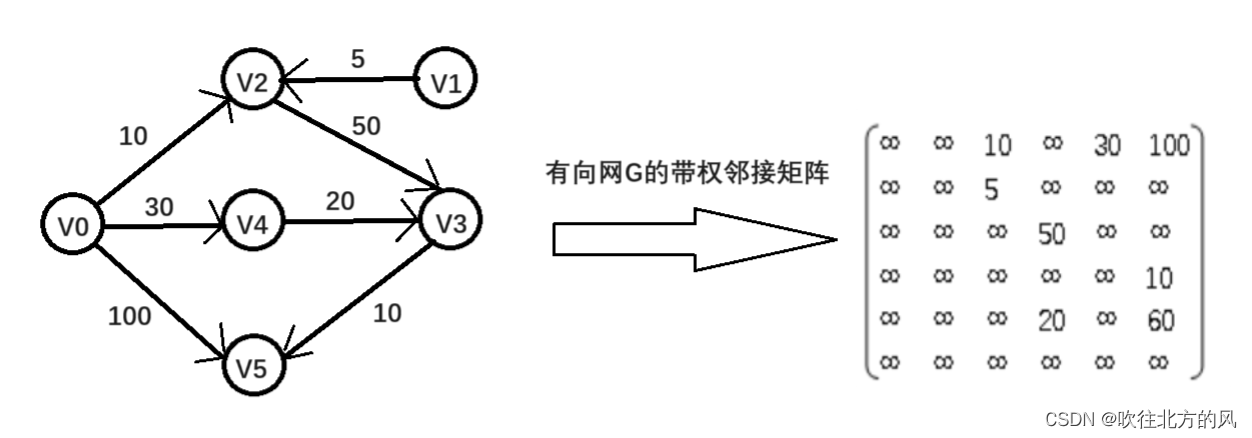
先给出算法代码，然后结合着代码来讲可能会更容易理解：

/* 迪杰斯特拉（Dijkstra) 算法*/
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc path, ShortPathTable dist)
{int v, w, k, min;int final[MaxVerterNum];		// final[w] = 1表示求得顶点 v0 至 vw的最短路径，即已访问过顶点vwfor (v = 0; v < G.vexNum; v++){final[v] = 0;				// 全部顶点初始化为未知最短路径状态dist[v] = G.Edge[v0][v];	// 将与v0点有连线的顶点加上权值path[v] = -1;				// 初始化路劲数组p为-1}dist[0] = 0;	// v0至v0路径为0final[0] = 1;	// v0至v0不需要路径/* 开始主循环，每次求得v0到某个顶点v的最短路径*/for (v = 1; v < G.vexNum; v++){min = INFINITY;		// 当前所知离v0顶点的最近距离for (w = 0; w < G.vexNum; w++)	// 寻找离v0最近的顶点{if (!final[w] && dist[w] < min){k = w;min = dist[w];	// w顶点离v0顶点更近}}final[k] = 1;	// 将目前找到的最近的顶点置为1for (w = 0; w < G.vexNum; w++)	// 修正当前最短路径及距离{/* 如果经过v顶点的路径比现在这条路径的长度短的话 */if (!final[w] && (min + G.Edge[k][w] < dist[w])){dist[w] = min + G.Edge[k][w];	// 修改当前路径长度path[w] = k;}}}
}

【1】初始化（执行上述代码前面一部分）

⚠️注意：这里的path[2] 、path[4]、path[5]没有初始化为0，主要是没必要，因为path[i] = -1，就表明 i 的前驱结点一定就是V0。

final[i]：标记各顶点是否已找到最短路径
dist[i]：最短路径长度
path[i]：路径上的前驱

    int v, w, k, min;int final[MaxVerterNum];  // final[w] = 1表示求得顶点 v0 至 vw的最短路径，即已访问过顶点vwfor (v = 0; v < G.vexNum; v++){final[v] = 0;		// 全部顶点初始化为未知最短路径状态dist[v] = G.Edge[v0][v]; // 将与v0点有连线的顶点加上权值path[v] = -1;		// 初始化路劲数组p为-1}dist[0] = 0;			// v0至v0路径为0final[0] = 1;			// v0至v0不需要路径

【2】找到距离V0最近的顶点，并修改当前路径长度

/* 开始主循环，每次求得v0到某个顶点v的最短路径*/for (v = 1; v < G.vexNum; v++){min = INFINITY;		// 当前所知离v0顶点的最近距离for (w = 0; w < G.vexNum; w++)	// 寻找离v0最近的顶点{if (!final[w] && dist[w] < min){k = w;min = dist[w];	// w顶点离v0顶点更近}}final[k] = 1;			// 将目前找到的最近的顶点置为1for (w = 0; w < G.vexNum; w++)	// 修正当前最短路径及距离{/* 如果经过v顶点的路径比现在这条路径的长度短的话 */if (!final[w] && (min + G.Edge[k][w] < dist[w])){dist[w] = min + G.Edge[k][w];	// 修改当前路径长度path[w] = k;}}}