二叉树之堆的应用

堆排序

思路详解

Ⅰ 建堆

Ⅱ 利用堆的删除思想来进行排序

功能接口

向上调整算法

向下调整算法

主函数

运行结果展示

TOP - K问题

思路详解

Ⅰ 用数据集合中前K个元素来建堆

Ⅱ 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

功能接口

建小堆所需的向上调整算法

向下调整算法

创建数据集合的文件创建接口

堆排序接口

TOP-K

运行结果展示

结语

堆排序

所谓堆排序，即是使用堆的思想来进行排序。

在堆中，我们逻辑上想象他是一棵树，但实际在物理上它是一个数组。

思路详解

Ⅰ 建堆

如果我们要将数据升序排列，那我们需要建大堆，如果降序排列，则建小堆。

升序：建大堆；

降序：建小堆。

Ⅱ 利用堆的删除思想来进行排序

以升序为例，假设此时我们已经完成了大堆的创建。

还记得堆是如何删除的吗？

我们将堆顶与堆尾互换，然后删除堆尾，再向下调整。

但在堆排序中，我们互换之后并不删除堆尾，只是不再对堆尾进行操作。

试想，一个大堆，堆顶元素自然是最大的数据，当我们交换堆顶堆尾，最大的元素就到了堆尾，我们不再对其进行操作，逻辑上将其暂时剥离数组，随后再进行向下调整。循环往复。

我们来画图看看：

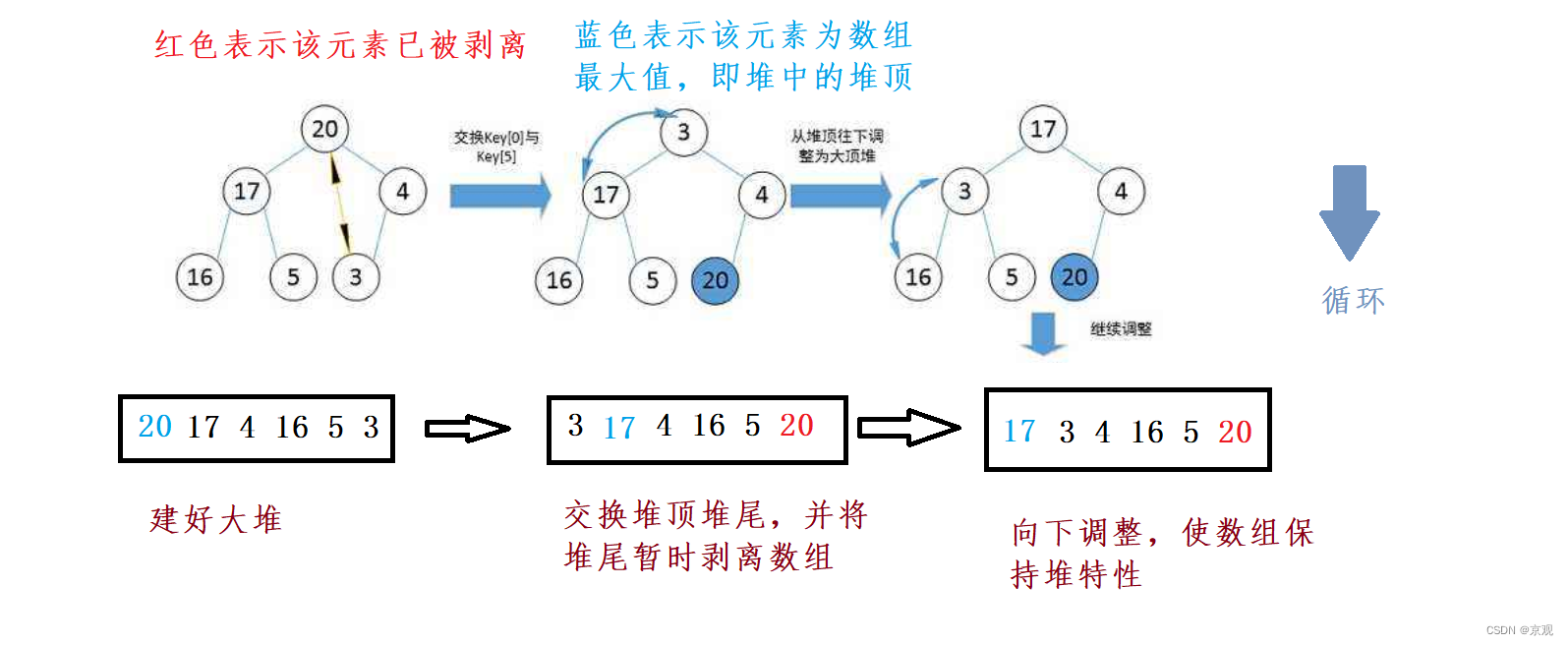
功能接口

有关堆的一些基础特性可查看我的另一篇文章。数据结构之树 --- 二叉树-CSDN博客

向上调整算法

该接口建堆时使用。

//小堆
void SmaADjustUP(int* a, int child)
{int parent = (child - 1) / 2;while (child >= 0){if (a[child] < a[parent]){swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}elsebreak;}
}

向下调整算法

void SmaADjustDown(int *a,int size,int parent)
{int child = parent * 2 + 1;while (child < size){if (child+1 < size && a[child] > a[child + 1]){child = child + 1;}if (a[child] < a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}elsebreak;}
}

当然，只使用向下调整算法也是可以的。

主函数

步骤操作在代码中有注释。

int main()
{int a[10] = { 2,5,3,9,6,8,7,1,10 };int len = 10;for (int i = 0; i < len; i++)//建堆{BigADjustUP(a,i);}while(len>0){swap(&a[0], &a[len - 1]);//交换堆顶与堆尾BigADjustDown(a, len - 1, 0);//向下调整，注意此时传入的数组大小为len-1，并未将堆尾传入//即向下调整时不包括堆尾len--;//剥离堆尾}for (int i = 0; i < 10; i++)//打印操作{printf("%d ", a[i]);}return 0;
}

运行结果展示

TOP - K问题

TOP-K问题：即求数据集合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，

思路详解

Ⅰ 用数据集合中前K个元素来建堆

前k个最大的元素，则建小堆
前k个最小的元素，则建大堆

Ⅱ 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

以建小堆为例，我们要求前5个最大的元素。

假设此时我们已经建好5个元素的小堆，将剩余的元素依次与堆顶进行比较，如果大于堆顶，则与堆顶交换，然后进行向下调整算法，使堆时刻保持特性。直至集合中的数据全部比较完成，此时堆中的五个数就是数据集合中最大的五个数。

我们来看看例子

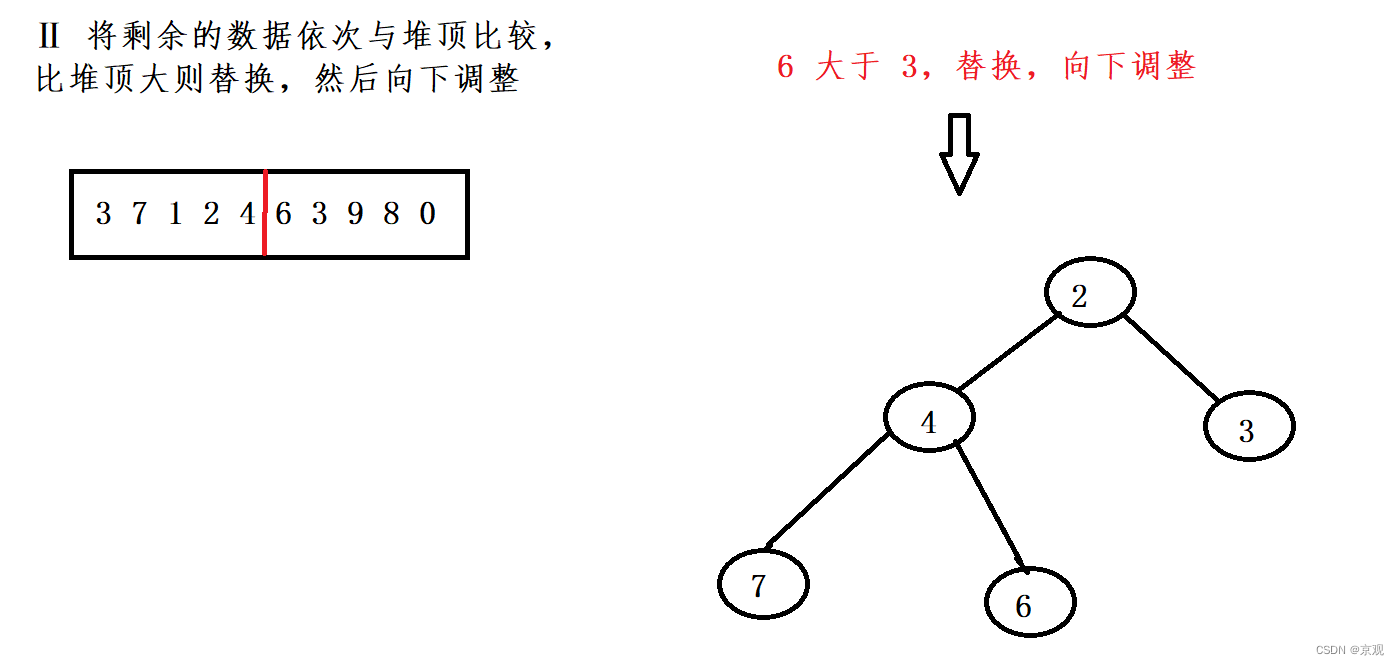
按照上图方法比对，直至数据集合结束。

功能接口

建小堆所需的向上调整算法

向下调整算法

以上两个函数接口在堆排序中已经给出来了。

创建数据集合的文件创建接口

由于TOP-K问题一般用来处理大数据，因此我们需要创建一个乱序的含有大量数据的数据集合。

我们创建一个文件，向文件内写入一定数量的随机值，然后对文件中的数据进行操作。

void CreateFile(int n)
{srand(time(0));//const char* file = "data.txt";FILE* fin = fopen("data.txt", "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; i++){int num = (rand() + i) % 10000;fprintf(fin, "%d\n", num);}fclose(fin);
}

该过程我们需要用到 rand() 函数。

堆排序接口

将最后小堆中的数据进行升序排列

void heapSort(int* a, int len)
{int size = len;for (int i = 0; i < size; i++){swap(&a[0], &a[len - 1]);SmaADjustDown(a, len - 1, 0);len--;}for (int i = 0; i < size; i++){if (i % 5 == 0)printf("\n");printf("%d ", a[i]);}
}

TOP-K

在该函数中，我们调用创建文件接口，完成数据集合文件的创建，然后取k个数建堆。

接下来将剩下的数据依次与堆顶比对，向下调整。

void PrintTopk(int n,int k)
{CreateFile(n);//创建数据集合的文件FILE* fout=fopen("data.txt", "r");if (fout == NULL){perror("fopen errorPrint");return;}int* a = (int*)malloc(sizeof(int) * k);//开辟堆空间for (int i = 0; i < k; i++)//建k个数的堆{fscanf(fout,"%d",&a[i]);SmaADjustUP(a, i);}int tmp = 0;while (fscanf(fout, "%d", &tmp)!=EOF)//直至文件内的数据取完{if (tmp > a[0]){a[0] = tmp;SmaADjustDown(a, k, 0);}}heapSort(a, k);free(a);fclose(fout);
}