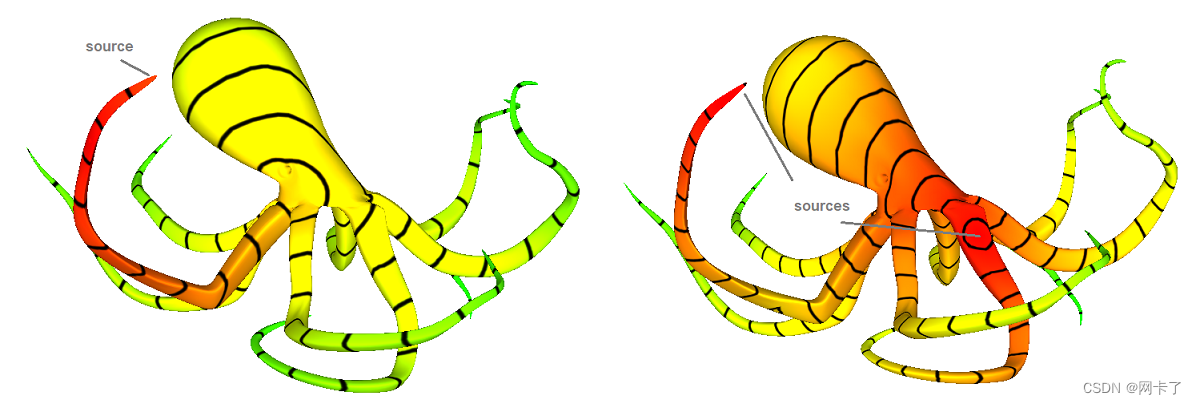
1、介绍

        热方法是一种算法，通过返回三角形网格中所有顶点到给定源顶点集合中最近顶点的测地距离近似值，解决单源或多源最短路径问题。网格中两个顶点的测地距离是指从网格表面（可能经过面的内部）行进的距离。例如，在章鱼的两个相邻臂上，三维空间中靠近的两个顶点可能在表面上很远。在图中，我们使用渐变的红色/绿色对距离进行着色编码，对应于接近/远离源顶点。

        热方法非常高效，因为该算法简化为两个标准的稀疏线性代数问题。在需要对固定域进行重复距离查询的情况下，该方法特别有用，因为第一次查询的预计算可以重复使用。

        一般来说，该方法在Delaunay三角形网格上表现良好，尽管在实践中对于远离Delaunay的网格也可能表现良好。为了确保良好的性能，我们启用了预处理步骤，该步骤构建了内在Delaunay三角剖分（iDT）；这个剖分不会改变输入几何体，但通常会提高解决方案的质量。该预处理步骤的成本大约会使总预处理成本翻倍。

        内在Delaunay三角剖分（Intrinsic Delaunay Triangulation，IDT）

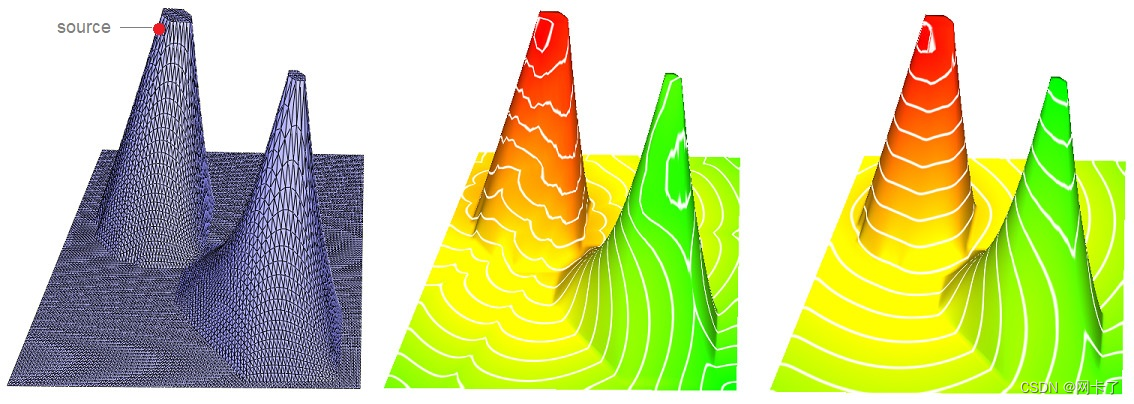
在不进行iDT重网格和进行iDT重新网格的情况下放置在网格上的等值线。

        在下一节中，我们给出了一些例子。理论背景部分介绍了热方法的数学理论。最后一节是关于实施历史。

        请注意，此软件包依赖于第三方 Eigen 库（3.3 或更高版本）或概念 SparseLinearAlgebraWithFactor Traits_d 的其他模型。。

        此软件包与三角曲面网格最短路径软件包相关。两者都处理测地线距离。热方法软件包为网格的每个顶点计算到一或多个源顶点的近似距离。测地线最短路径软件包计算曲面任意两点之间的精确最短路径。 

2、理论背景

        “热方法算法”一节概述了热方法所需的理论。“内蕴Delaunay三角化”一节介绍了内蕴Delaunay三角化所需的背景。

2.1、加热法

        关于热方法的详细概述，读者可以参考[1]阅读原文。在接下来的内容中，我们将介绍一些基本概念，以便解释我们的算法。一般来说，热方法适用于任何设置，如果存在一个梯度算子，一个发散算子和一个拉普拉斯算子 Δ=∇⋅∇Δ；这是向量微积分的标准导数。

        热处理方法包括三个主要步骤：

        将热流u˙=Δu整合；在某个固定的时间 t；求向量场X=−∇ut/|∇ut|；求解泊松方程 Δϕ=∇⋅X

        函数 ϕ 是到给定源集的距离的近似值，并且随着 t 趋近于零而接近真实距离。 然后，必须通过用近似值替换空间和时间中的导数，将该算法转化为离散算法。

        热方程可以用一个向后欧拉步进行时间离散化。这意味着必须求解以下方程

        (id−tΔ)ut=δγ(x)，其中δγ(x)是狄拉克δ函数，编码“无限”热尖峰（如果x在源集γ中，则为1，否则为0），其中id是单位算子。

        空间离散化取决于离散表面表示的选择。对于这个包，我们只使用三角形网格。设u∈R|V|表示一个在三角表面上的分段线性函数，该三角表面有V个顶点、E条边和F个面。在顶点i处的拉普拉斯算子的标准离散化是

        Lui=12Ai∑j(cotαij+cotβij)(uj−ui)，其中Ai是所有与顶点i相交的三角形的面积的三分之一。

        该和值由所有相邻顶点 j 计算得出。此外，αij 和 βij 是与相应边 ij 对角的角度。我们通过矩阵 L=M−1Lc 表示这一操作，其中 M∈R|V|x|V| 是一个包含顶点面积的对角矩阵，Lc∈R|V|x|V| 是余切算子，表示剩余的和值。

        由此，对称正定系统（M−tLC）u=δγ可以求解，以找到u，其中δγ是γ上的克罗内克δ。
接下来，给定三角形中的梯度可以表示为

        ∇u=12Af∑iui(N×ei)

        其中 Af 是三角形的面积，N 是其外单位法线，ei 是第 i 条边向量（逆时针方向），ui 是 u 在相对顶点的值。与顶点 i 相关的积分散度可以表示为

        ∇⋅X=12∑jcotθ1(e1⋅Xj)+cotθ2(e2⋅Xj)

        其中，总和是针对每个具有向量Xj的入射三角形j求得的，e1和e2是包含i的三角形j的两个边向量，θ1和θ2是相对角。

        最后，设b∈R|V|为归一化向量场X的积分散度。因此，求解对称泊松问题Lcϕ=b可以计算出最终的距离函数。

2.2、内在Delaunay三角剖分

        cotan Laplace 算子的标准离散化使用三角形网格中角度的余切。 内在的 Delaunay 算法构造了相同多面体的三角剖分，这反过来又产生了不同的（通常更精确的）cotan Laplace 算子。从概念上讲，iDT 的边缘仍然连接原始（输入）表面上的对顶点，但现在允许沿着多面体是测地线路径，并且不必对应于输入三角剖分的边缘。这些路径不是显式存储的；相反，我们只是在三角剖分更新时跟踪它们的长度。这些长度足以确定内在三角形的面积和角度，进而确定新的 cotan Laplace 矩阵。

        如果对角之和不小于 pi，或者等价地，如果对角之余切线为非负数，则网格的边缘是局部 Delaunay。如果网格的所有边缘都是局部 Delaunay，则网格是 Delaunay。

        将给定的平面三角剖分转换为Delaunay三角剖分的标准算法是翻转网格中的非Delaunay边，直到网格为Delaunay。同样，单形表面的内在Delaunay三角剖分是通过执行内在边翻转来构造的。

        设 K=(V,E,T) 是一个二维流形三角形网格，其中 V 是顶点集，E 是边集，T 是面集（三角形集）。设 L 是欧几里得距离集，其中 L(eij)=lij=||pi−pj||，其中 pi 和 pj 分别是顶点 i 和 j 在 R3 中的位置。然后，将 (K,L)作为输入输入到 iDT 算法中，该算法返回 (K~,L~)，即内在 Delaunay 网格和内在长度。该算法如下：

 for all edge e in E : Mark(e)Stack s <-- Ewhile !Empty(s) doedge(ij) = Pop(s) and Unmark(edge(ij))if !Delaunay(edge(ij)) thenedge(kl) = Flip(edge(ij)) and compute the new length length(kl) using the Cosine Theoremfor all edge e in {edge(kj), edge(jl), edge(li), edge(ik)} doif !Mark(e) thenMark(e) and Push(s,e)end ifend forend ifend while
return (~K,~L)

        然后，新的（K，L）被用来像往常一样实现热方法。

        我们在开始时已经举了一个例子，其中内禀Delaunay三角化改进了结果。网格是通过给2D三角化赋予高程而获得的，这导致了高度细长的三角形。

        这种情况类似于任何具有非常小角度面的三角形网格，如下图所示。

放置在没有iDT重新网格的网格上的等值线

 

使用iDT重新网格化放置在网格上的等值线

3、性能

        算法的时间复杂度主要由线性求解器的选择决定。在目前的实施方案中，Cholesky预系数约为O（N1.5）距离的计算大致为O（N），其中N是三角测量中的顶点数。该算法使用两个N×N
矩阵，两者都具有相同的非零模式（平均每行/列7个非零）。计算成本与源集的大小无关。基运算包括稀疏数值线性代数（双精度）和基本算术运算（包括平方根）。

        我们在英特尔酷睿i7-7700HQ 2.8HGz上执行基准测试，并使用Visual Studio 2013进行编译。

Number of triangles	Initialization iDT (sec)	Distance computation iDT (sec)	Initialization Direct (sec)	Distance computation Direct (sec)
30,000	0.18	0.02	0.12	0.01
200,000	1.82	1.31	1.32	0.11
500,000	10.45	0.75	8.07	0.55
1,800,000	38.91	2.24	35.68	1.1

4、其他

        CGAL::Heat_method_3::estimate_geodesic_distances 是一个用于估计三维空间中给定源集的内在测地距离的函数。它使用热方法（heat method）来求解测地距离问题。

        该函数接受一个三维三角形网格作为输入，其中每个三角形由三个顶点表示。它还接受一个源集，表示要计算测地距离的目标点集。

        函数的工作原理如下：首先，它在三角形网格上定义一个初始温度场，其中每个顶点的温度初始化为无穷大。然后，它使用向后欧拉步（backward Euler step）对热方程进行离散化，以更新温度场。在每个时间步长中，函数计算每个顶点处的梯度，并根据梯度更新温度值。随着时间的推移，温度值逐渐接近测地距离，最终收敛到稳定状态。函数返回收敛后的温度场，其中每个顶点的温度值即为该顶点到源集的测地距离。

        该函数使用了一些数学公式和概念来计算测地距离，包括拉普拉斯算子、梯度、散度和离散化等。这些公式和概念在数学和物理中有广泛的应用，特别是在计算几何和数值分析领域。

        总结：CGAL::Heat_method_3::estimate_geodesic_distances 是一个用于估计三维空间中给定源集的测地距离的函数，它使用热方法进行求解。该函数通过离散化热方程并计算梯度来逼近测地距离，最终返回收敛后的温度场作为结果。

        CGAL::Heat_method_3::Surface_mesh_geodesic_distances_3 是一个用于计算三维网格上点到源集的测地距离的函数，它使用热方法进行求解。该函数通过离散化热方程并计算梯度来逼近测地距离，最终返回收敛后的温度场作为结果。