声明：本文的部分内容参考了他人的文章。在编写过程中，我们尊重他人的知识产权和学术成果，力求遵循合理使用原则，并在适用的情况下注明引用来源。
本文主要参考了《PostgresSQL数据库内核分析》一书，OpenGauss1.1.0 的开源代码和《OpenGauss数据库源码解析》一书以及OpenGauss社区学习文档

概述

  遗传算法（GA）是一种启发式搜索算法，用于解决优化和搜索问题，它借鉴了自然界中的进化理论。在数据库领域，遗传算法可以用于各种任务，如查询优化、数据挖掘、模式识别等。以下是遗传算法在数据库中应用的一些关键概念：

1. 种群（Population）：在遗传算法中，一个种群由多个个体组成，每个个体代表数据库中的一个潜在解决方案。
2. 染色体（Chromosome）：每个个体由染色体表示，它是解决方案的编码。在数据库应用中，染色体可能代表查询计划、数据库索引的配置或数据分布的模式。
3. 适应度函数（Fitness Function）：这是一个评价函数，用于确定染色体的优劣。在数据库中，适应度函数可能基于查询执行时间、资源使用效率或数据检索的准确性。
4. 选择（Selection）：算法选择适应度较高的个体进行繁殖。这意味着更好的解决方案有更高的机会被保留下来。
5. 交叉（Crossover）：选择的个体通过交叉操作生成新的后代。这类似于生物遗传中的DNA交换，可以在数据库解决方案中引入新的组合。
6. 变异（Mutation）：为了维持遗传多样性并避免局部最优解，算法会随机改变某些后代的某些部分。在数据库应用中，这可能意味着改变查询计划的某个操作或索引结构。

  在 PostgreSQL 中遗传算法主要用在连接路径的生成操作中，其流如下图所示。

  遗传算法让 PostgreSQL查询规划器可以通过非穷举搜索有效地支持很多表的连接路径的生成。PostgreSQL 使用遗传算法（Genetic Query Optimizer，GEQO）来优化某些类型的复杂查询，尤其是涉及多个连接的查询。当查询涉及多个表连接时，可能的连接顺序成指数级增长，传统的优化器可能在这种情况下效率低下。这时，PostgreSQL 的 GEQO 模块就派上用场了。下面是 GEQO 在 PostgreSQL 中的一般执行过程。

GEQO 的执行过程

1. 初始化种群：GEQO 首先生成一个初始种群。这个种群包含了多个个体，每个个体代表一个可能的连接顺序。
2. 适应度计算：对于种群中的每个个体，GEQO 使用成本估算模型来计算它的适应度。适应度通常是基于预计的查询成本，成本越低表示个体越适合。
3. 选择：基于适应度，GEQO 选择较优的个体用于产生下一代。
4. 交叉：通过交叉操作，从选中的个体中创建新的后代。交叉可以看作是将两个查询计划的部分组合起来形成新的查询计划。
5. 变异：在一些后代中随机引入变化，以增加遗传多样性。
6. 新一代种群：通过选择、交叉和变异，生成新的种群，代替旧的种群。
7. 终止条件：这个过程重复进行，直到达到一定的代数或其他终止条件。
8. 最佳个体选择：最终，选出适应度最高的个体作为查询计划。

下面将对其中的个体编码方式、适应值、父体选择策略等进行介绍。

个体的编码方式及种群初始化

  PostgreSQL 中用遗传算法解决表连接问题的方式类似于解决 TSP 问题可能的连接路径被当作整数串进行编码。每个串代表查询中可能的一种连接顺序。例如，下图中的查询树是用整数串 “4132” 编码的，也就是说，首先联接表 “4” 和 “1”，得到的结果表和表 “3” 连接，最后再和表 “2” 连接。这里的 1、2、3、4 都是 PostgreSQL 里的关系标识 (relids)。

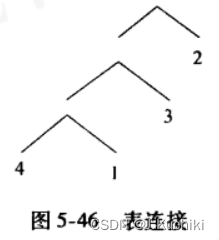
  遗传算法执行的第一步是随机初始化种群，种群大小的计算方法参考后面。设种群大小为 n，首先随机初始化 n 个排列，即 n 个类似于上面提到的字 “4132”，每一个排列数就是个个体。然后基于 n 个排列数生成基本表的连接路径，在此过程中会进行代价评估，将最后的代价作为适应值来衡量该个体的优劣。每一个个体都用 Chromosome 结构表示，其中记录了该个体的排列数和代价。Chromosome 结构如下所示：

typedef int Gene;
typedef struct Chromosome {Gene* string;	//染色体的数据值Cost worth;		//对该染色体的代价评估值
} Chromosome;

geqo 函数

  geqo 是数据库查询优化问题的遗传算法解决方案，类似于旅行推销员问题（TSP）的遗传算法。函数源码如下所示：（路径：src\gausskernel\optimizer\geqo\geqo_main.cpp）

/* geqo 函数：解决查询优化问题，类似于受限的旅行推销员问题（TSP） */
RelOptInfo* geqo(PlannerInfo* root, int number_of_rels, List* initial_rels)
{/* 初始化相关变量 */GeqoPrivateData priv;int generation;Chromosome* momma = NULL;Chromosome* daddy = NULL;Chromosome* kid = NULL;Pool* pool = NULL;int pool_size, number_generations;#ifdef GEQO_DEBUGint status_interval;
#endifGene* best_tour = NULL;RelOptInfo* best_rel = NULL;/* ... 条件编译部分省略 ... *//* 设置私有信息 */root->join_search_private = (void*)&priv;priv.initial_rels = initial_rels;/* 初始化私有随机数生成器 */geqo_set_seed(root, u_sess->attr.attr_sql.Geqo_seed);/* 设置遗传算法（GA）参数 */pool_size = gimme_pool_size(number_of_rels);number_generations = gimme_number_generations(pool_size);/* 分配遗传池内存 */pool = alloc_pool(root, pool_size, number_of_rels);/* 随机初始化遗传池 */random_init_pool(root, pool);/* 根据最便宜路径的适应度对池进行排序 */sort_pool(root, pool);/* 分配染色体 momma 和 daddy 的内存 */momma = alloc_chromo(root, pool->string_length);daddy = alloc_chromo(root, pool->string_length);/* ... 条件编译部分省略 ... *//* 迭代优化主体部分 */for (generation = 0; generation < number_generations; generation++) {/* 选择操作：使用线性偏差函数 */geqo_selection(root, momma, daddy, pool, u_sess->attr.attr_sql.Geqo_selection_bias);/* ... 不同交叉操作的条件编译部分省略 ... *//* 评估适应度 */kid->worth = geqo_eval(root, kid->string, pool->string_length);/* 根据其价值将子代加入生存竞争 */spread_chromo(root, kid, pool);/* ... 调试信息的条件编译部分省略 ... */}/* ... 最优解的提取和内存清理部分省略 ... */return best_rel;
}

适应值

  个体的适应值等于该个体中 N 个表的连接代价（参考表间的连接方式）。适应值计算由函数 geqo_eval 实现。包括以下步骤：

1. 个体有效。
2. 确定个体的连接次序以及连接方式。
3. 计算个体的适应值。

  计算个体的适应值时，首先要检查个体是否有效。也就是说，对一个给定的个体，能不能把这个个体中的表按照某种次序连接起来，因为有些表之间是不能连接的。如果一个个体按任何次序都不能连接，那么这么个体是无效的。对于有效的个体，还要确定连接次序和连接方式。在连接次序和连接方式确定之后才能计算个体的适应值。

geqo_eval 函数

  geqo_eval 函数的作用是评估查询计划的适应度，即计算给定查询计划的成本。在遗传算法中，这个步骤是关键的，因为它决定了哪些染色体（查询计划）更适合生存并被用于后续的交叉和变异。

主要步骤如下：

1. 创建临时内存上下文： 由于 geqo_eval 会被多次调用，因此创建一个临时内存上下文用于存储临时数据，防止内存泄漏。
2. 构建最佳路径： 使用 gimme_tree 函数根据提供的基因序列（即查询计划的一种表示）构建最佳查询路径。
3. 计算适应度： 计算构建的查询路径的总成本，作为这个查询计划的适应度。
4. 恢复原始状态： 将 root->join_rel_list 和 root->join_rel_hash 恢复到函数调用前的状态，以保持数据的一致性。
5. 释放内存资源： 释放在函数执行过程中分配的所有内存资源。

  geqo_eval 函数代码如下所示：（路径：src\gausskernel\optimizer\geqo\geqo_eval.cpp）

/** geqo_eval** 返回作为种群中个体的查询树的成本。*/
Cost geqo_eval(PlannerInfo* root, Gene* tour, int num_gene)
{MemoryContext mycontext;  // 用于临时存储的私有内存上下文MemoryContext oldcxt;     // 保存旧的内存上下文RelOptInfo* joinrel = NULL;  // 指向连接关系的指针Cost fitness;  // 适应度（成本）int savelength;  // 用于保存原始 join_rel_list 的长度struct HTAB* savehash;  // 保存原始的哈希表/** 创建一个私有内存上下文，用于存储 gimme_tree() 内部分配的所有临时存储。** 由于 geqo_eval() 会被多次调用，我们不能让所有这些内存直到语句结束才被回收。* 注意我们使临时上下文成为规划器正常上下文的子节点，这样即使我们通过 ereport(ERROR) 中止，* 它也会被释放。*/mycontext = AllocSetContextCreate(CurrentMemoryContext, "GEQO", ALLOCSET_DEFAULT_MINSIZE, ALLOCSET_DEFAULT_INITSIZE, ALLOCSET_DEFAULT_MAXSIZE);oldcxt = MemoryContextSwitchTo(mycontext);/** gimme_tree 会向 root->join_rel_list 添加条目，这可能已经包含了一些条目。* 新增加的条目将被下面的 MemoryContextDelete 回收，因此我们必须确保在退出前将列表恢复到其原始状态。* 我们通过将列表截断为原始长度来实现这一点。注意这假设任何添加的条目都被附加在了末尾！** 我们还必须确保不搞乱外部的 join_rel_hash（如果有的话）。* 我们可以通过临时将链接设置为 NULL 来实现。（如果我们正在处理足够多的连接关系，* 这很可能是的，那么一个新的哈希表将被建立并在本地使用。）** join_rel_level[] 不应该在使用中，所以只需断言它不是。*/savelength = list_length(root->join_rel_list);savehash = root->join_rel_hash;AssertEreport(root->join_rel_level == NULL, MOD_OPT, "");root->join_rel_hash = NULL;/* 为给定的关系组合构建最佳路径 */joinrel = gimme_tree(root, tour, num_gene);/** 计算适应度** XXX geqo 目前不支持针对部分结果检索的优化——如何修复？*/fitness = ((Path*)linitial(joinrel->cheapest_total_path))->total_cost;/** 将 join_rel_list 恢复到原来的状态，并恢复原来的哈希表（如果有的话）。*/root->join_rel_list = list_truncate(root->join_rel_list, savelength);root->join_rel_hash = savehash;/* 释放 gimme_tree 内部获取的所有内存 */(void)MemoryContextSwitchTo(oldcxt);MemoryContextDelete(mycontext);return fitness;
}

gimme_tree 函数

  gimme_tree 函数的作用是根据遗传算法中生成的基因序列（代表表连接的顺序）来构建查询计划。它不单纯按照基因序列的顺序直接连接表，而是考虑了启发式规则和实际的语义限制，以形成有效且合法的查询计划。gimme_tree 函数的源码如下所示：（路径：src\gausskernel\optimizer\geqo\geqo_eval.cpp）

主要步骤如下：

1. 初始化： 创建一个空的 “块” 列表，用于保存已成功连接的关系。
2. 按顺序处理关系： 遍历基因序列中的每个元素（代表一个表），并将其转化为一个单独的关系块。
3. 合并块： 尝试将新的关系块合并到现有的块中，如果不能合并，就将其作为新的块添加到列表中。
4. 处理剩余块： 一旦基因序列被完全处理，对于未能合并的块，使用强制合并策略尝试形成一个完整的连接关系。
5. 检查结果： 检查是否成功地将所有表连接为一个单一的查询计划。如果失败，报告错误。

/** gimme_tree*    根据指定的顺序形成查询规划的估算。**    'tour' 是提议的连接顺序，长度为 'num_gene'**    返回一个新的连接关系，其最便宜路径是这个连接顺序的最佳计划。*/
RelOptInfo* gimme_tree(PlannerInfo* root, Gene* tour, int num_gene)
{GeqoPrivateData* priv = (GeqoPrivateData*)root->join_search_private;List* clumps = NIL;  // 保存成功连接关系的“块”的列表int rel_count;/** 有时候，由于启发式规则或实际的语义限制，一个关系还不能加入到其他关系。* 我们维护一个成功连接关系的“块”的列表，大的块在前面。* 从 tour 中获取的每个新关系都被添加到它能够连接的第一个块中；* 如果没有，它就成为自己的新块。当我们扩大一个现有块时，* 我们检查它是否现在可以和其他块合并。在 tour 全部扫描完后，* 我们忽略启发式规则，尝试强制合并剩余的块。*/clumps = NIL;for (rel_count = 0; rel_count < num_gene; rel_count++) {int cur_rel_index;RelOptInfo* cur_rel = NULL;Clump* cur_clump = NULL;/* 获取下一个输入关系 */cur_rel_index = (int)tour[rel_count];cur_rel = (RelOptInfo*)list_nth(priv->initial_rels, cur_rel_index - 1);/* 将其变成单关系块 */cur_clump = (Clump*)palloc(sizeof(Clump));cur_clump->joinrel = cur_rel;cur_clump->size = 1;/* 将其合并到块列表中，仅使用合适的连接 */clumps = merge_clump(root, clumps, cur_clump, false);}if (list_length(clumps) > 1) {/* 强制合并剩余的块 */List* fclumps = NIL;ListCell* lc = NULL;foreach (lc, clumps) {Clump* clump = (Clump*)lfirst(lc);fclumps = merge_clump(root, fclumps, clump, true);}clumps = fclumps;}/* 检查是否成功形成单个连接关系 */if (list_length(clumps) != 1)ereport(ERROR,(errmodule(MOD_OPT),errcode(ERRCODE_OPTIMIZER_INCONSISTENT_STATE),errmsg("failed to join all relations together")));return ((Clump*)linitial(clumps))->joinrel;
}

  让我们通过一个具体的数据库查询优化案例来描述 gimme_tree 函数的工作流程。假设我们有一个数据库查询任务，涉及四个表：Orders, Customers, Products, Suppliers。查询的目的是获取所有订单，包括客户信息、产品信息和供应商信息。

场景设定

  假设遗传算法为这个查询生成了一个基因序列（表连接顺序）

1. Customers
2. Orders
3. Products
4. Suppliers

  这个顺序代表了遗传算法认为可能是高效的表连接顺序。

初始化和处理关系
gimme_tree 函数开始工作：

1. 初始化“块”列表： 开始时，没有任何关系被连接，因此 “块” 列表为空。
2. 按顺序处理关系：

• 首先尝试将 Customers 表加入一个新的块。
• 接下来，尝试将 Orders 表加入到 Customers 块中。如果基于启发式规则或语义限制，Orders 不能直接与 Customers 连接，则它将成为一个新的独立块。
• 然后，尝试将 Products 表加入到已有的块中。这一步同样会考虑连接的合法性和有效性。
• 最后，尝试将 Suppliers 表加入到一个合适的块中。

强制合并剩余块

  在处理完所有表之后，如果存在多个独立的块，gimme_tree 函数将尝试强制将这些块合并成一个单一的查询计划。这可能涉及重新考虑先前由于启发式规则而未执行的连接。

生成最终查询计划

• 如果成功，函数将返回一个 RelOptInfo 结构，表示包含所有四个表的单一最佳连接计划。
• 如果由于语义限制等原因无法将所有表合并成一个单一查询计划，函数将报告错误。

  在这个案例中，gimme_tree 函数演示了如何灵活地根据遗传算法提供的表连接顺序来构建查询计划。它不仅遵循算法提议的顺序，还考虑实际的连接限制和优化策略，以确保生成的查询计划既合法又高效。通过这种方式，函数能够处理包括复杂的灌木状（bushy）计划在内的各种查询场景。

父体选择策略

  父体选择策略采用基于排名的选择策略，选择概率函数如公式 5-2 所示。其中，max 是个体总数，bias 的默认值为 2.0，geo_rand 是 0.0~1.0 之间的随机数，f(geo_rand)表示当前个体在种群中的编号（该编号是根据当前个体的适应值在种群中的排名来确定）。该函数表明，排名越靠前的个体被选择的概率越大。不过在 PostgreSQL 8.4.1 的实现中父体选择时没有考虑 A 小于 0 的情况。

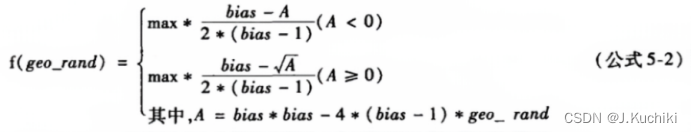
geqo_selection 函数

  其中，geqo_selection 函数实现了遗传算法中的 “选择” 步骤，其目的是从基因池（染色体集合）中选择两个染色体作为后续交叉过程的父本和母本。geqo_selection 函数的作用是在遗传算法中从一个基因池（一组染色体）中选择两个染色体，以便进行后续的遗传操作（如交叉）。这个选择过程是基于一定的偏好（由参数 bias 指定），通常旨在选择适应度较高的染色体，从而增加产生更优后代的机会。

函数主要步骤如下：

1. 随机选择：使用线性随机选择方法（linear_rand）基于偏好从基因池中随机选择两个染色体。
2. 确保不同：检查两次选择是否得到了不同的染色体。如果选择了相同的染色体，并且基因池大小大于1，则重新选择第二个染色体。
3. 复制染色体：将选中的两个染色体复制到 momma 和 daddy，这两个染色体将被用作后续交叉过程的父本和母本。

  下面是对这段代码的详细中文注释以及对其功能的描述：（路径：src\gausskernel\optimizer\geqo\geqo_selection.cpp）

/** geqo_selection*   根据输入参数描述的偏好，从基因池中选择第一和第二基因*/
void geqo_selection(PlannerInfo* root, Chromosome* momma, Chromosome* daddy, Pool* pool, double bias)
{int first, second;// 使用线性随机函数选择第一个染色体的索引first = linear_rand(root, pool->size, bias);// 使用线性随机函数选择第二个染色体的索引second = linear_rand(root, pool->size, bias);/** 确保选择了不同的基因，除非池大小只有一个，在这种情况下不能这样做。** 当平台的 erand48() 实现有问题时，这段代码会陷入无限循环。* 现在我们总是使用自己的版本。*/if (pool->size > 1) {// 如果选择了相同的染色体，则重新选择第二个染色体，直到它与第一个不同while (first == second)second = linear_rand(root, pool->size, bias);}// 将选择的第一个染色体复制到 mommageqo_copy(root, momma, &pool->data[first], pool->string_length);// 将选择的第二个染色体复制到 daddygeqo_copy(root, daddy, &pool->data[second], pool->string_length);
}

杂交算子

  PostgreSQL 中的遗传算法提供了边重组杂交、部分匹配杂交、循环杂交、基于位置的杂交和顺序杂交等多种杂交算子，用于从父辈种群中产生新的后代个体，默认使用的是边重组杂交算法。

边重组杂交 ERX ( edge recombination crossover)

  边重组杂交算子由函数 gimme_edge_table 和 gimme_tour 实现。函数 gimme_edge_table 用来计算边关系，如步骤 1 和步骤 2 ** 所示；函数 gimme_tour 由边关系得到后代，如步骤 3 **所示。
  接下来我们来看看书中对边重组杂交算子的描述吧：

gimme_edge_table 函数

  gimme_edge_table 函数的作用是在遗传算法的边缘重组交叉（ERX）中构建边缘表。这个表记录了两个 “基因”（在这里是旅行路径）之间的所有可能的边缘连接，从而帮助算法理解哪些边缘在两个基因中是共享的。这对于找出最优的新路径组合非常重要。
  函数主要步骤如下：

1. 初始化边缘表：首先清除边缘表中的旧数据，为新数据做准备。
2. 填充新数据：

• 遍历每个基因的每个点（城市），考虑到路径是环形的，即最后一个点连接回第一个点。
• 对于每一对相邻点（城市），在边缘表中记录它们之间的边。
• 因为边是双向的，所以每对点的连接需要记录两次。

3. 计算平均边数：计算每个城市的平均边数，这个数字反映了两个基因之间边的多样性。数值在 2.0（边均匀分布）到 4.0（边多样分布）之间。

  通过这种方式，gimme_edge_table 函数为遗传算法提供了一个关键的数据结构，使算法能够有效地进行边缘重组交叉，从而生成更优的查询计划或旅行路径。这在处理复杂的优化问题，如数据库查询优化或旅行推销员问题时，是非常有用的。函数源码如下所示：（路径：src\gausskernel\optimizer\geqo\geqo_erx.cpp）

/* gimme_edge_table**   填充表示两个输入基因中点之间的显式边集合的数据结构。**   假设环形游览和双向边。**   gimme_edge() 会将“共享”边设置为负值。**   返回每个城市的平均边数，范围在 2.0 - 4.0，*   其中 2.0=均匀；4.0=多样。**/
float gimme_edge_table(PlannerInfo* root, Gene* tour1, Gene* tour2, int num_gene, Edge* edge_table)
{int i, index1, index2;int edge_total; // 两个基因中唯一边的总数/* 首先清除边表的旧数据 */for (i = 1; i <= num_gene; i++) {edge_table[i].total_edges = 0;edge_table[i].unused_edges = 0;}/* 用新数据填充边表 */edge_total = 0;for (index1 = 0; index1 < num_gene; index1++) {/** 假设路径是环形的，即 1->2, 2->3, 3->1* 这个操作将 n 映射回 1*/index2 = (index1 + 1) % num_gene;/** 边是双向的，即 1->2 和 2->1 是相同的* 对每条边调用 gimme_edge 两次*/edge_total += gimme_edge(root, tour1[index1], tour1[index2], edge_table);gimme_edge(root, tour1[index2], tour1[index1], edge_table);edge_total += gimme_edge(root, tour2[index1], tour2[index2], edge_table);gimme_edge(root, tour2[index2], tour2[index1], edge_table);}/* 返回每个索引的平均边数 */return ((float)(edge_total * 2) / (float)num_gene);
}

gimme_tour 函数

  这段代码 gimme_tour 是遗传算法中用于根据边缘表创建新的基因序列（或称为旅行路径）的函数。gimme_tour 函数的目的是创建一个新的基因序列，即确定表连接的新顺序。它首先随机选择一个起始点（表），然后按照边缘表中的信息依次选择下一个连接点（表）。在选择过程中，函数优先选择共享边，即那些在多个父基因中都存在的边。如果在选择过程中遇到无法使用的边（如无剩余未使用的边），函数将尝试处理这种故障情况，并继续构建基因序列。函数最后返回在构建新基因序列过程中遇到的边缘失败次数。函数源码如下所示：（路径：src\gausskernel\optimizer\geqo\geqo_erx.cpp）

/* gimme_tour**   使用边缘表中的边创建一个新的基因序列。*   优先考虑“共享”边（即所有父基因都拥有的边，在边缘表中被标记为负值）。**/
int gimme_tour(PlannerInfo* root, Edge* edge_table, Gene* new_gene, int num_gene)
{int i;int edge_failures = 0; // 记录边缘失败的数量/* 在 1 到 num_gene 之间随机选择一个起始点 */new_gene[0] = (Gene)geqo_randint(root, num_gene, 1);for (i = 1; i < num_gene; i++) {/** 将每个点加入到基因序列中时，从边缘表中移除该点*/remove_gene(root, new_gene[i - 1], edge_table[(int)new_gene[i - 1]], edge_table);/* 为新加入的点找到下一个目的地 */if (edge_table[new_gene[i - 1]].unused_edges > 0)new_gene[i] = gimme_gene(root, edge_table[(int)new_gene[i - 1]], edge_table);else { /* 处理失败情况 */edge_failures++;/* 在发生故障时选择下一个点 */new_gene[i] = edge_failure(root, new_gene, i - 1, edge_table, num_gene);}/* 标记这个节点已经被包含在内 */edge_table[(int)new_gene[i - 1]].unused_edges = -1;}return edge_failures;
}

变异算子

  变异算子由函数 geqo_mutation 实现，该函数随机地从父体中产生两个变异位，交换这两个变异位的值，执行 numgene（基因数目）次这样的交换操作。如下所示：

geqo_mutation 函数

  geqo_mutation 函数通过随机交换基因序列中元素的位置来引入变异。这种随机变异帮助算法探索解空间的不同区域，防止过早收敛到局部最优解，增加找到全局最优解的机会。变异操作在遗传算法中是重要的，因为它提供了额外的随机性和多样性。函数源码如下所示：（路径：src\gausskernel\optimizer\geqo\geqo_mutation.cpp）

void geqo_mutation(PlannerInfo* root, Gene* tour, int num_gene)
{int swap1;int swap2;int num_swaps = geqo_randint(root, num_gene / 3, 0); // 随机确定变异次数Gene temp;while (num_swaps > 0) { // 执行多次变异操作swap1 = geqo_randint(root, num_gene - 1, 0); // 随机选择第一个要交换的位置swap2 = geqo_randint(root, num_gene - 1, 0); // 随机选择第二个要交换的位置while (swap1 == swap2) // 确保两个交换位置不同swap2 = geqo_randint(root, num_gene - 1, 0);temp = tour[swap1]; // 执行交换操作tour[swap1] = tour[swap2];tour[swap2] = temp;num_swaps -= 1; // 减少剩余的变异次数}
}