【机器学习】西瓜书学习心得及课后习题参考答案—第6章支持向量机
1.试证明样本空间中任意点x到超平面(w,b)的距离为式(6.2)。
首先,直观解释二维空间内点到直线的距离:

由平面向量的有关知识,可得:
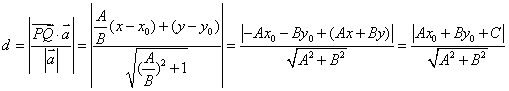
超平面的法向量为 w w w,任取平面上一点 x 0 x_0 x0,则超平面可以表示为 ω T ⋅ x 0 + b = 0 ω^T \cdot x_0 + b = 0 ωT⋅x0+b=0。一个点 x x x到超平面的距离可以用该点到 x 0 x_0 x0 的距离在法向量 (ω) 方向上的投影来表示,即:
距离 = ∣ ω T ( x − x 0 ) ∣ ∣ ∣ ω ∣ ∣ = ∣ ω T x + b ∣ ∣ ∣ ω ∣ ∣ \text{距离} = \frac{|ω^T(x−x_0)|}{||ω||} = \frac{|ω^T x + b|}{||ω||} 距离=∣∣ω∣∣∣ωT(x−x0)∣=∣∣ω∣∣∣ωTx+b∣
其中:
- ω T ω^T ωT 表示向量 w w w 的转置。
- ∣ ∣ ω ∣ ∣ ||ω|| ∣∣ω∣∣ 表示向量 w w w 的范数(模长)。
- x x x 是指向平面上的任意点。
- x 0 x_0 x0 是平面上的某一点。
- b b b 是平面的偏置项。
这个公式表示了点 x x x 到平面的距离,计算方式是将点 x x x 投影到法向量 ω ω ω 上,然后除以 ω ω ω 的模长。
其中 ω = ( ω_1; ω_2; … ; ωd) 为法向量,决定了超平面的方向 ; b b b 为位移项,决定
了超平面与原点之间的距离.
)











 -- 流量控制 和 拥塞控制)



protobuf基础)


