Matlab
利用随机梯度方法进行辨识的举例,可以结合不同情况进行优化处理(例如需要复现文献中结果)
Matlab代码如下:
clc;clear;close; format short g;
M = 'Stochastic gradient method';
sigma = 0.5; % Noise standard deviation
FF = 0.88; % Forgetting factor
PlotLength = 3000; length1 = PlotLength + 200;
na = 4; nb = 4; n = na + nb; % order
alp = [1, 0, -0.96, 0, 0.64]; bet = [0.412, 0.9682, 0.824, 0.2472]; d = [1];
par0 = [alp(2 : na + 1), bet(1 : nb)]';
p0 = 1e6; P = eye(n) * p0; r = 1; % initial value
par1 = ones(n, 1) * 1e-6;sy = f_integral(alp, bet); sv = f_integral(alp, d); % the complex integral
delta_ns = sqrt(sv / sy) * 100 * sigma; % the noise to signal ratio
[sy, sv, delta_ns];u = normrnd(0, 1, length1, 1);
v = normrnd(0, sigma, length1, 1);
Gz = tf(bet, alp, 1);
Gn = tf(d, alp, 1);
y = lsim(Gz, u) + lsim(Gn, v);%% Stochastic gradient
jj = 0; j1 = 0;
for k = 20 : length1jj = jj + 1;varphi = [-y(k - 1: -1: k - na); u(k - 1: -1: k - nb)]; r = FF * r + varphi' * varphi; % SGpar1 = par1 + varphi / r * (y(k) - varphi' * par1); %L = P * varphi / (FF + varphi' * P *varphi); % RLS%P = P - L * varphi' * P;%par1 = par1 + L * (y(k) - varphi' * par1);delta = norm(par1 - par0) / norm(par0);sg(jj, :) = [jj, par1', delta];if (jj == 100) | (jj == 200) | (jj == 500) | mod(jj, 1000) == 0j1 = j1 + 1;sg_100(j1, :) = [jj, par1', delta * 100];endif jj == PlotLengthbreakend
end
sg_100(j1 + 1, :) = [0, par0', 0];%fprintf('\n', 't & \t a_1 & \t a_2 & \t b_1 & \t b_2 & \delta');
fprintf('%6d & %6.3f & %6.3f & %6.3f & %6.3f & %6.3f & %6.3f & %6.3f & %6.3f & %6.3f \\\\ \n', sg_100');
figure(1)
jk = (19: 10: PlotLength - 1)';
plot(sg(jk, 1), sg(jk, n + 2));xlabel('\it k'); ylabel('{\it \delta}');仿真结果图:

随着迭代次数的增加,可见误差越来越小,命令行窗口输出如下:
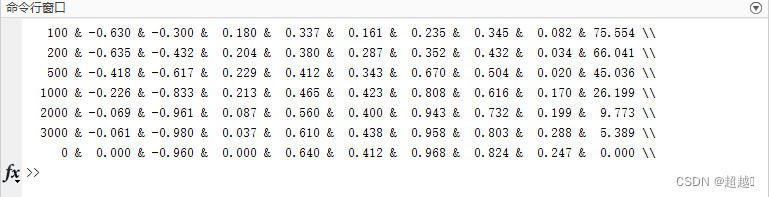
尝试修改参数加深理解~

)
)




已解决)



)





中的证书没有右三角,无法导出p12文件)

