1 简介

当信号的频率信息是已知的，或者近似已知的，则采样频率容易选择，选择最大采样频率的2倍以上(奈奎斯特采样)。

这里，将讨论信号频率未知的情况。尤其是，考虑如何避免混叠错误。

2 低通滤波(反混叠)

去除混叠错误的最佳方法是在采集数值数据前对信号进行滤波：

• 一般使用低通滤波。低通滤波通常叫做抗混叠滤波。
• 低通滤波让低频信息通过，则将指定频率分量剪除。
• 理想的低频滤波会将高频信息剪除，高于某个频率的内容全部删除。
• 一般低通滤波的频率阈值选择采样频率的 1/2，$f_{cutoff}=f_s/2$。
• 至此，混叠信息被去除，可以进行数值采样。

不幸的是，现实生活中的低通滤波器不会突然切断高频；相反，更高频率的衰减随着频率而相当缓慢地下降。

正因为如此，大多数真实的数据采集系统采用比采样频率小几倍的截止频率来确保适当的抗混叠。

3 使用不同的采样频率采样

尽管没有低通抗混叠滤波，则可以使用多种不同的采样频率进行采样，以及对相应的频率谱进行采样。如果使用2种采样频率，频谱的峰值则处于不同位置，则可以确定存在混叠误差。这种情况需要提高采样频率知道峰不变，则混叠峰可以被解释，后面有样例说明。

在许多实际应用中，例如测量流体流中的湍流波动，有时频谱中没有明显的峰值；相反，存在对频谱有贡献的宽范围的频率。在这种情况下，看到的不是尖锐的峰值，而是频谱中的宽起伏。如果采样频率足够高，则频谱应在频谱的折叠频率附近向零振幅下降。否则，没有以足够高的频率进行采样，并且信号的高频分量可能会导致混叠误差。

以上技术会在下面的案例中说明。

4 案例

以电压信号进行说明，伴随着随机噪声。首先，我们不知道信号频率分量，但预计频率在 15Hz。使用多个频率进行采样。第一个案例的采样频率在 $f_s=30Hz，N=256$，如下图所示。

从图中可以看出：

• 可以看到在 10Hz 处有很强的分量，振幅在 0.8v，还有一个很强的分量在 5.7Hz，振幅在 1.2v。
• 因为采样时间是任意的，因此存在泄漏。
• 其他的频率谱显示存在噪声

这个谱是值得信任的吗？是否存在混叠误差？最佳验证方式是采用更高的采样频率。

这里注意，新的采样频率不能是前面采样频率的整数倍如 60Hz/90Hz，否则混叠误差一样会出现。

我们选择 66Hz，N=256，采样时间从 8.5s 缩减到 3.9s，具体如下图所示：

从图中可以看出：

• 10Hz 仍然是峰值，但是 5.7Hz 消失了，取而代之的是 30.3Hz，混叠误差仍然存在，可见采样频率还是不够高。

对这两个例子进行探索，看其是否具有一致性：

• 66Hz 的采样频率在 30.3Hz 处获得了频率分量
• 因为 66Hz 比 2*30.3=60.6Hz 大，这可能是信号的合法频率分量。
• 如果是合法的，则第一个案例能够预测混叠成分。假设 30.3Hz 的频率分量是真实的，则：

$$f_a=｜f-f_s\cdot NINT(f/f_s)｜=｜30.3-30.0\cdot NINT(30.3/30.0)｜=0.3Hz$$

由上式可知，0.3 与 5.7Hz 不一致，所以 66Hz 还不够高。

为此，重新选了 100Hz (96不合适，因为96=30+66) 进行采样，如下图所示：

从图上可以看出：

• 10Hz 仍然是一个强分量，因此我们可以确定其是真实的。但另一个峰35.7 Hz 出现，则5.7和30.3都不是真实的。
• 假设35.7是真实存在的，则可以通过 66Hz 的采样频率计算获得：

$$f_a=｜f-f_s\cdot NINT(f/f_s)｜=｜35.7-66.0\cdot NINT(35.7/66)｜=30.3Hz$$

上式结果显示两者是一致。

再来看看 30Hz 的采样频率计算：

$$f_a=｜f-f_s\cdot NINT(f/f_s)｜=｜35.7-30.0\cdot NINT(35.7/30)｜=5.7Hz$$

从上面两个式子可以得出，100Hz 是足够的，10Hz 和 35.7Hz 是成分，其他是噪声。

最后再检查一下，选用 125Hz 采样频率：

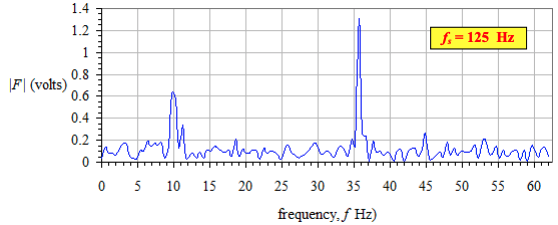
现在可以看出，10Hz 和 35.7Hz 的峰被保留。可以很自信的认为采样频率避免了混叠。

5 为什么一开始不选用高采样频率？

• 因为一开始就选用较大的采样频率，则无法确定峰是真实的还是混叠的。
• 采样频率过高会失去高频率信息。
• 低通滤波时，截止频率会设置过高，导致噪声过多。

参考：
https://www.me.psu.edu/cimbala/me345/Lectures/Frequency_Content_of_Signal.pdf