第十部分欧拉图与哈密顿图

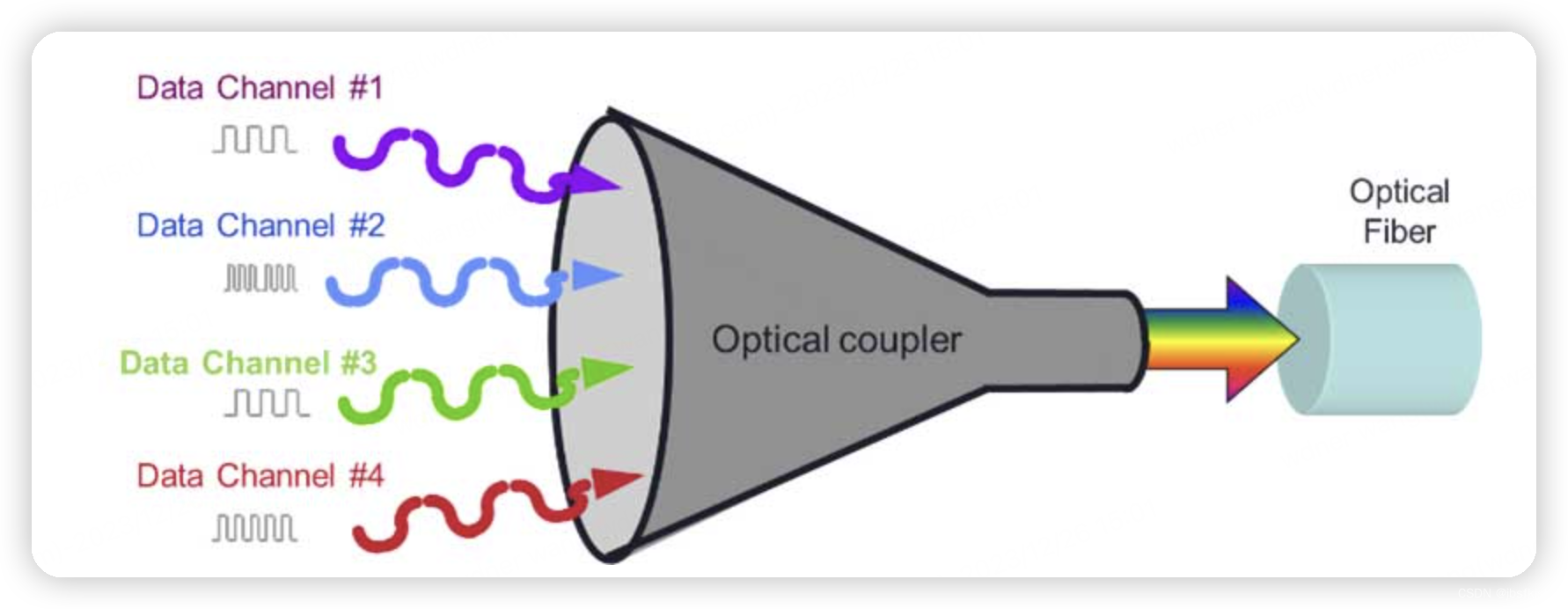
欧拉图：

历史背景：

哥尼斯堡七桥问题与欧拉图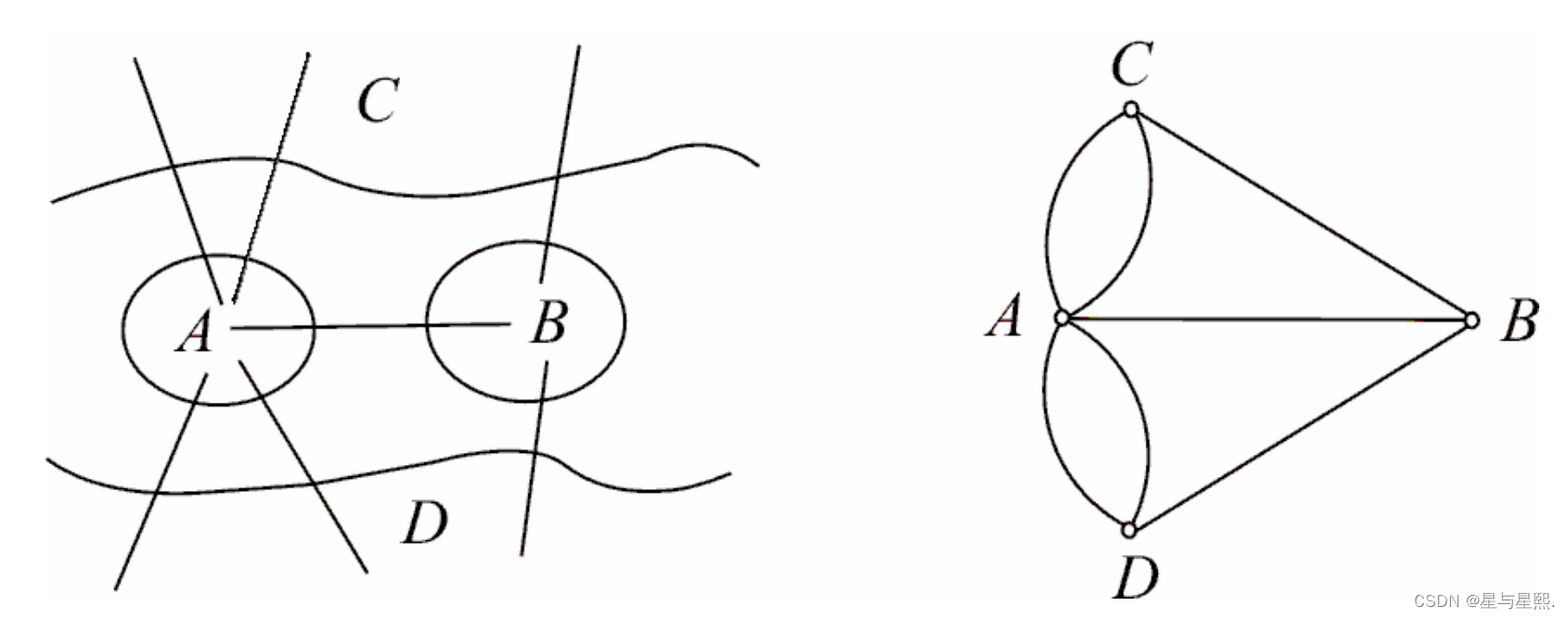

问题提出后，很多人对此很感兴趣，纷纷进行试验，但在相当长的时间里，始终未能解决。而利用普通数学知识，每座桥均走一次，那这七座桥所有的走法一共有7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040（种）。而这么多情况，要一一试验，这将会是很大的工作量。但怎么才能找到成功走过每座桥而不重复的路线呢？因而形成了著名的“哥尼斯堡七桥问题”。

定义 10.1

(1) 欧拉通路 —— 经过图中每条边一次且仅一次行遍所有顶 点的通路

(2) 欧拉回 路 —— 经过图中每条边一次且仅一次行遍所有顶 点的回路

(3) 欧拉图 —— 具有欧拉回路的图

(4) 半欧拉图 —— 具有欧拉通路而无欧拉回路的图

几点说明：

规定平凡图为欧拉图

欧拉通路是生成的简单通路，欧拉回路是生成的简单回路

环不影响图的欧拉性

定理 10.1 无向图 G 是欧拉图当且仅当 G 连通且无奇度数顶点

定理 10.2 无向图 G 是半欧拉图当且仅当 G 连通且恰有两个奇 度顶点

定理 10.3 有向图 D 是欧拉图当且仅当 D 是强连通的且每个顶 点的入度都等于出度

定理 10.4 有向图 D 是半欧拉图当且仅当 D 是单向连通的，且 D 中恰有两个奇度顶点，其中一个的入度比出度大 1 ，另一个 的出度比入度大 1 ，而其余顶点的入度都等于出度

定理 10.5 G 是非平凡的欧拉图当且仅当 G 是连通的且为若干 个边不重的圈之并

了解一下

Fleury算法：

(1) 任取 v 0 ∈ V ( G ) ，令 P 0 = v 0

(2) 设 P i = v 0 e 1 v 1 e 2 … e i v i 已经行遍，按下面方法从 E ( G ) − { e 1 , e 2 ,…, e i } 中选取 e i +1

(a) e i +1 与 v i 相关联

(b) 除非无别的边可供行遍，否则 e i +1 不应该为 G i = G − { e 1 , e 2 ,…, e i } 中的桥

(3) 当 (2) 不能再进行时，算法停止

可以证明算法停止时所得简单通路 P m = v 0 e 1 v 1 e 2 … e m v m ( v m = v 0 ) 为 G 中一条欧拉回路

哈密顿图：

历史背景：

哈密顿周游世界问题与哈密顿图

1859 年爱尔兰数学家威廉·哈密顿(William Hamilton) 提出一个“环游世界” 游戏: 把一个正十二面体的二十个顶点看作世界上著名的二十个城市，如第一个图, 要求游戏者找出一条路线, 沿着正十二面体的棱边访问每个城市恰好一次后回到出发点, 即环游世界. 这个游戏在欧洲风靡一时,哈密顿还以 25 个金币的高价把这个游戏的版权卖给了一个玩具商

定义10.2

(1) 哈密顿通路 —— 经过图中所有顶点一次仅一次的通路

(2) 哈密顿回路 —— 经过图中所有顶点一次仅一次的回路

(3) 哈密顿图 —— 具有哈密顿回路的图

(4) 半哈密顿图 —— 具有哈密顿通路且无哈密顿回路的图

几点说明：

平凡图是哈密顿图

哈密顿通路是初级通路，哈密顿回路是初级回路

环与平行边不影响哈密顿性

哈密顿图的实质是能将图中的所有顶点排在同一个圈上

例题

以下哪些是欧拉图，半欧拉图，哈密顿图，半哈密顿图

从上到下从左到右标号为(a),(b),(c),(d),(e),(f)

欧拉图：(a),(d)

半欧拉图：(b)

哈密顿图：(a),(b),(c),(d)

半哈密顿图：(e)

都不属于：(f)

最短路问题与货郎担问题

定义 10.3 给定图 G = < V , E > ， ( G 为无向图或有向图 ) ，设 W : E → R (R 为实数集 ) ，对 G 中任意边 e = ( v i , v j ) ( G 为有向图 时， e = < v i , v j >) ，设 W ( e ) = w ij ，称实数 w ij 为边 e 上的权 ，并将 w ij 标注在边 e 上，称 G 为 带权图 ，此时常将带权图 G 记作 < V , E , W >

设 G =< V , E , W > 为一个 n 阶完全带权图 K n ，各边的权非负，且 有的边的权可能为 ∞ . 求 G 中的一条最短的哈密顿回路，这就 是货郎担问题的数学模型