希尔排序详解（C语言）

前言
希尔排序是一种基于插入排序的快速排序算法。所以如果还会插入排序的小伙伴可以点击链接学习一下插入排序（点我点我！），相较于插入排序，希尔排序拥有更高的效率，小伙伴们肯定已经迫不及待学习了吧，那就让我们开始吧！
在这里插入图片描述

希尔排序
希尔排序的基本思想是将数组分割成若干个子序列进行插入排序，然后逐步缩小子序列的间隔，最终将整个数组变成一个有序序列。听起来很难理解对吧？那就让我给你们画个过程吧！
在这里插入图片描述
这是一组待排序的数据（从小到大排），我们首先要将这个序列分成若干个子序列，到底是多少个呢？希尔表示首先要定义一个增量gap（希尔认为应该为数组长度的一半，也有人认为应该是数组的长度的三分之一再+1，我们这里先按照希尔的思路进行讲解），然后按照增量gap分成若干组序列如图：
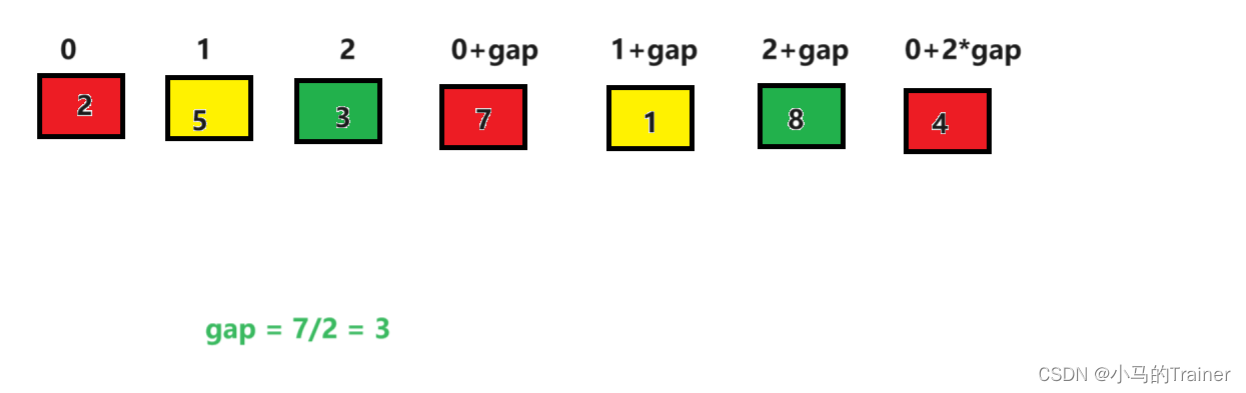
在这里插入图片描述
这样我们就将其分为了3组，然后每组内成员之间进行插入排序如图：

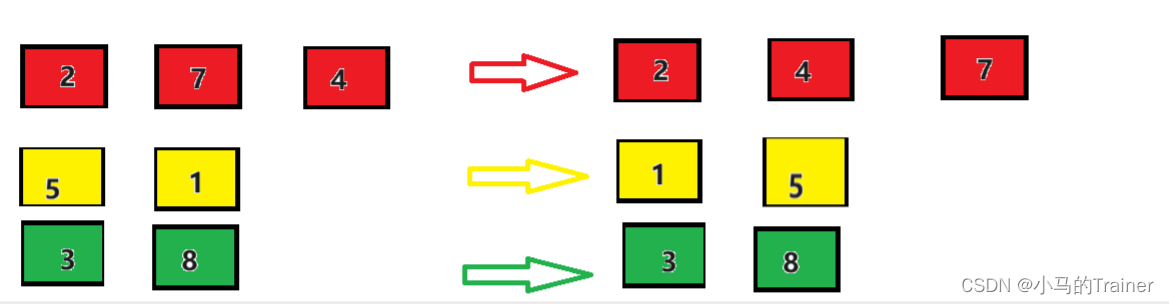
那么原数组就变成：

然后我们让gap/2，在进行新一轮的排序，当gap为1时，就相当于没有分组，直接进行插入排序，我们便可得到最终结果。每一轮排序之后数组就会变得更加有序，而且我们发现插入排序每一次移动只能移动一格，而希尔排序每次移动能移动gap格，所以效率肯定是正常插入排序不能比的。
那么我们要怎样对每一组进行插入排序呢？其实也很简单我们回想一下插入排序的代码是如何实现的：

for (int i = 0; i < size; i++)//size是数组长度{int end = i;//记录当前位置while (end){if (arr[end - 1] > arr[end])//交换位置{int tem = arr[end];arr[end] = arr[end - 1];arr[end-1] = tem;end--;}else//已经插入退出循环{break;}}}

这里我们是从0遍历到size-1，每次交换只交换一格，希尔排序也可以从开始就进行遍历，从0遍历到size-gap-1（因为我们要计较arr[end] 和 arr[end + gap]），每次交换交换gap格。只需要稍微修改一下插入排序的代码就可以实现希尔排序。
代码实现：

#include<stdio.h>
int main()
{int arr[10] = { 2, 0, 5, 2, 8, 1, 5, 1, 5, 6 };//定义一个数组int size = (int)(sizeof(arr) / sizeof(arr[0]));//数组的长度int gap = size;while (gap > 1)//当gap等于1时已经排好退出循环{gap /= 2;//每一轮gap都要除2for (int i = 0; i <= size - gap - 1; i++){int end = i;//记录当前位置while (end >= 0)//此时end可以等于0{if (arr[end] > arr[end + gap])//交换位置{int temp = arr[end];arr[end] = arr[end + gap];arr[end + gap] = temp;end -= gap;//后退gap格，反向遍历同一组的成员}elsebreak;}}}return 0;
}