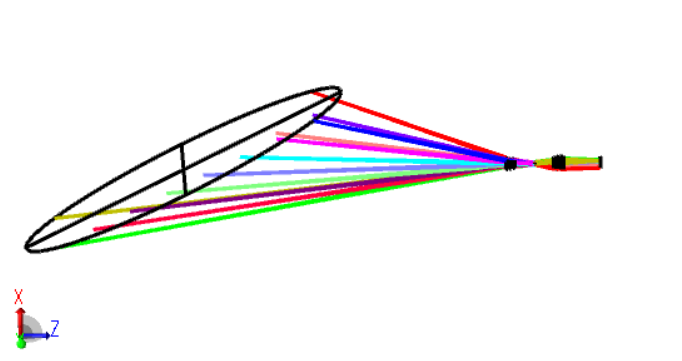
ZEMAX是广为使用的一款光学仿真软件，是进行光路设计和分析的利器；而相机标定，则是进行机器视觉任务时，拿到一款相机，对其实际参数进行确定的过程。
因此看起来，二者其实主要是针对不同的侧重点。前者主要面向相机开发，后者面向相机使用。
但是最近遇到了一个问题，不得不使用ZEMAX进行一些相机标定算法方面的验证。这期间遇到了一些问题，这里记录下来希望可以与大家分享，如有不对之处进请指正。
事情的经过是这样的：现在手头有一台特殊光路的相机，由于相机是课题组自己设计搭建，因此也有相应的ZEMAX工程文件。在理想情况下该相机与普通相机的成像模型完全一致，因此理论上可以使用张正义相机标定法进行标定。
然而，相机光路中包含一些特殊结构的光学元件，这些元件的安装与制造误差势必会为成像系统引入畸变，因此有必要为这些畸变和误差建立对应的数学模型，就类似于普通相机中的径向畸变与切向畸变模型，从而对其进行矫正。所以问题来了，怎么验证模型的可靠性呢？
仿真！
我的想法是这样的。在ZEMAX中对一些光学元件的角度进行一些微调，以此来模拟实际情况中的安装误差；接着在ZEMAX中模仿张正义标定法，在物方视场中设置类似棋盘格的视场：
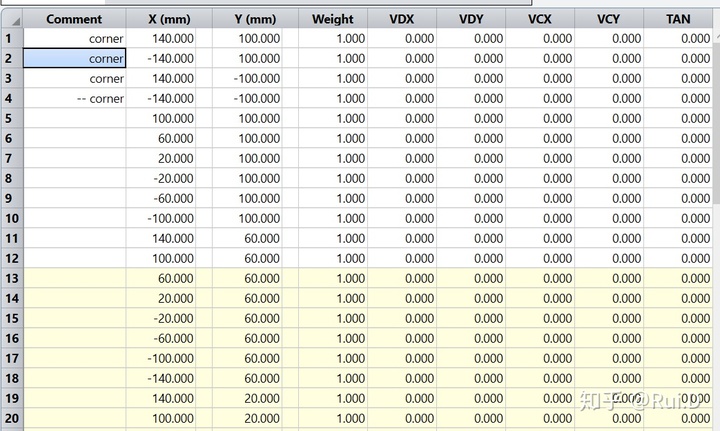
令成像系统在不同的位置与角度对物面成像，记录对应的像点。如此则得到了多组物点-像点的对应关系，接着使用张正义标定法再加上自己建立的误差模型对其进行标定，以此来验证自己的误差模型是否准确可靠。
OK，但是实际操作中，比较麻烦的地方就是“令成像系统在不同的位置与角度对物面成像”。下面就进入正题，说说我是怎么达到这个目的的。
一.旋转光学系统
当光路与视场都设定好之后，此时的3D视图是这样的：
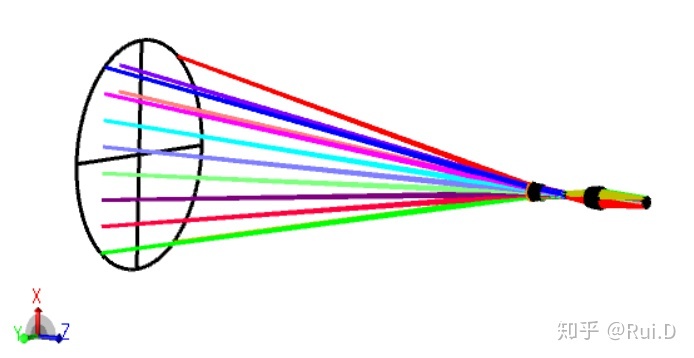
(吐槽一下，ZEMAX2017以后虽然最多可以设置超过2000个视场，但是只显示12个，如果视场中有48个视场点，需要重复设置4次才能完成所有成像)
进行相机标定的时候，我们需要在不同角度进行拍摄，因此首先想到的办法是旋转光学系统。
所以首先在物面之后添加坐标间断，设置旋转参数。
然后就成了这个样子：
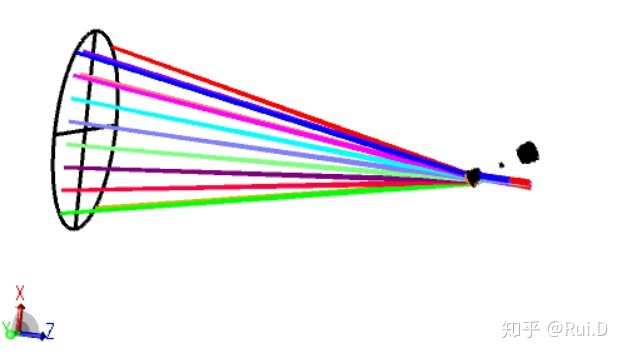
光线进入了成像系统，但是却没有穿过后续的元件。
这里有一个办法或许能解决这个问题：
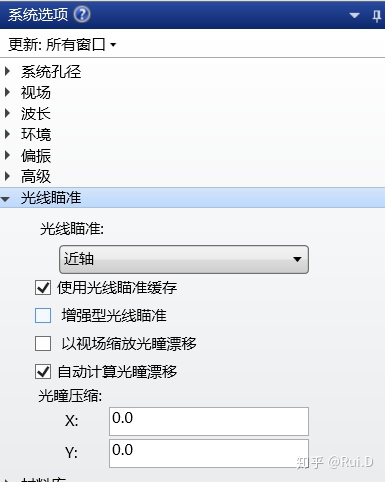
打开系统选项中的光线瞄准，这时：
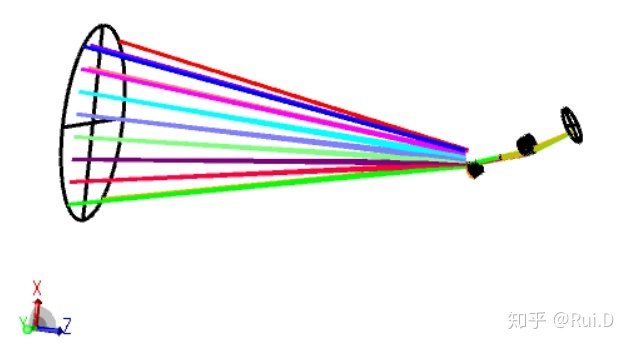
可以看到光线已经按照光轴进行了偏折，接着调整坐标间断中的偏心参数，令所有光线进入即可。
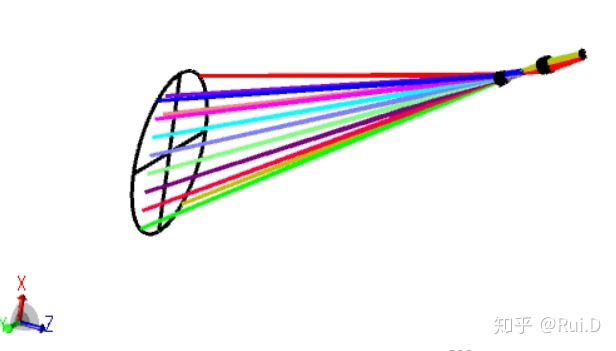
如果能顺利进行到这里的话，就已经大功告成了。但是我实际中遇到的问题是，当光路结构比较复杂的时候，在开启光线瞄准的情况下，输入倾斜角度经常会提示：
而且由于光线瞄准是软件进行迭代求解，如果一次输入大角度，同样也会提示上述错误。比如直接输入30°就会报错，但是连续输入10°、20°、30°可能就没有问题。
在我的光学结构中，即使输入很小的倾斜角度就会报错，因此上述方法无法使用
二.旋转物面
山不走来，那就走向山；既然旋转光学系统不行，那旋转物面呢？
ZEMAX中，物面可以设置为倾斜面，可以输入正切值改变物面的角度。
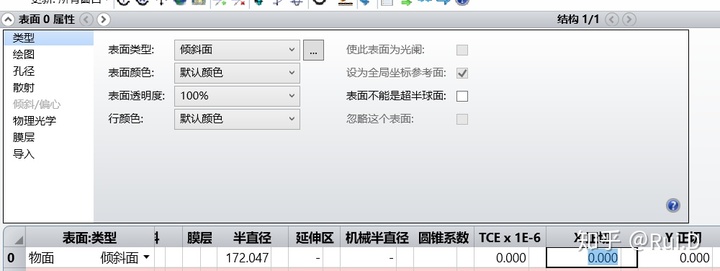
比如输入Y正切为2：
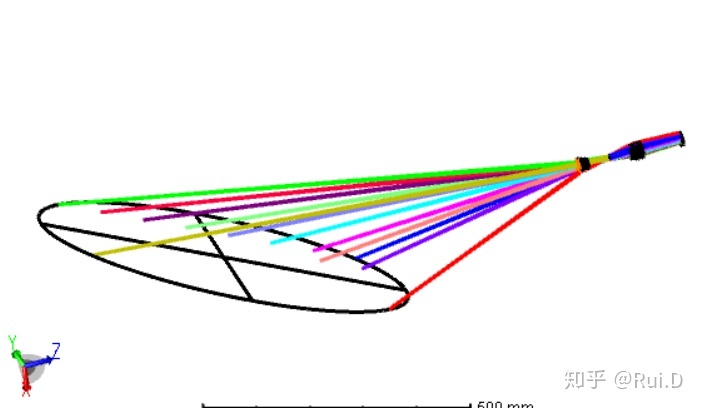
看起来好像不错的样子，但问题是，物面中各个视场之间的关系已经与之前不再相同了，之前我们设置视场的时候，是为每一个视场设定了一个平面坐标，但是旋转之后，虽然各个视场点仍在一个平面上，但是彼此之间的距离已经与之前不同了。
此时每个物面中的点，都成为一个三维点，x、y坐标是我们提前设置的，Z坐标为：
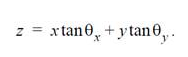
如果用这种方法进行相机标定，就类似于实际进行相机标定时，不同角度下拍摄不同的标定板。
但是仔细想想，张正义标定法中其实并没有限定标定板必须统一啊，拍一张换一个标定板也可以啊，只要确定标定板的尺寸和对应的像点就可以喽。
于是接下来的问题转换为：三维空间平面中的三维坐标，怎么转化成该平面二维坐标？
我的做法是这样的：
根据上述方程，显然这个平面的法向量是(tanθx，tanθy，-1)。
显然(1,0,tanθx)也在该平面上，对上述两个向量进行模为1的操作后，再进行叉乘得到了第三个向量。
这三个向量组成了旋转后平面的一组正交基。对这三个向量组成的矩阵取逆，就得到了原始物面与旋转之后物面的转换关系。
将该逆矩阵与三维空间平面中的三维坐标相乘，就得到了对应的平面二维坐标(其实也是三维坐标，只是最后一个维度数值为0)。
再结合该平面每个视场对应的像点，就可以进行标定了。
值得注意的是，MATLAB中相机标定函数中的世界坐标是固定的，但是我们这里相当于每张照片都不同，因此相应的标定代码需要进行一些修改，才可以完成相机标定。
