概念：

数据结构 : 数据用什么样的方式组合在一起。
数据结构是计算机存储数据的方式，指相互之间存在一种或多种特定关系的数据元素集合

常见数据结构：

数据存储的常用结构有：栈、队列、数组、链表和红黑树。

栈：

stack,又称堆栈，它是运算受限的线性表，其限制是仅允许在标的一端进行插入和删除操作，不允许在其
他任何位置进行添加、查找、删除等操作。

栈结构的特点：

先进后出（FILO）

• 压栈(进栈)：就是存元素。即，把元素存储到栈的顶端位置，栈中已有元素依次向栈底方向移动一个位置。
• 弹栈(出栈)：就是取元素。即，把栈的顶端位置元素取出，栈中已有元素依次向栈顶方向移动一个位置。

图解：

队列结构:

queue，简称队，它同堆栈一样，也是一种运算受限的线性表，其限制是仅允许在表的一端进行插入，而在表的另一端进行删除。

队列结构的特点：

先进先出（FIFO）,进和出是两个口，比如我们排队是不是先排的先拿到号离开

数组结构：

数组是一种查询快，增删慢的模型
在内存中，数组的数据连续存放，数据长度固定，这样知道数组开头位置和偏移量就可以直接计算出数据地址
查询数据通过地址值和索引定位，查询任意数据耗时相同，查询速度快
删除数据时，要将原始数据删除，同时后面每个数据前移，删除速度慢
添加数据时，添加位置的每个数据后移，再添加元素，添加速度慢

数组结构的特点：

链表结构：

链表：linked list，由一系列结点node（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。我们常说的链表，结构有单向链表与双向链表。

• 简单的说，采用该结构的集合，对元素的存取有如下的特点：

• 查找元素慢：想查找某个元素，需要通过连接的节点，依次向后查找指定元素
• 增删元素快：添加或者删除某个元素，只要更换上一个节点和下一个节点就可以了

单向链表：

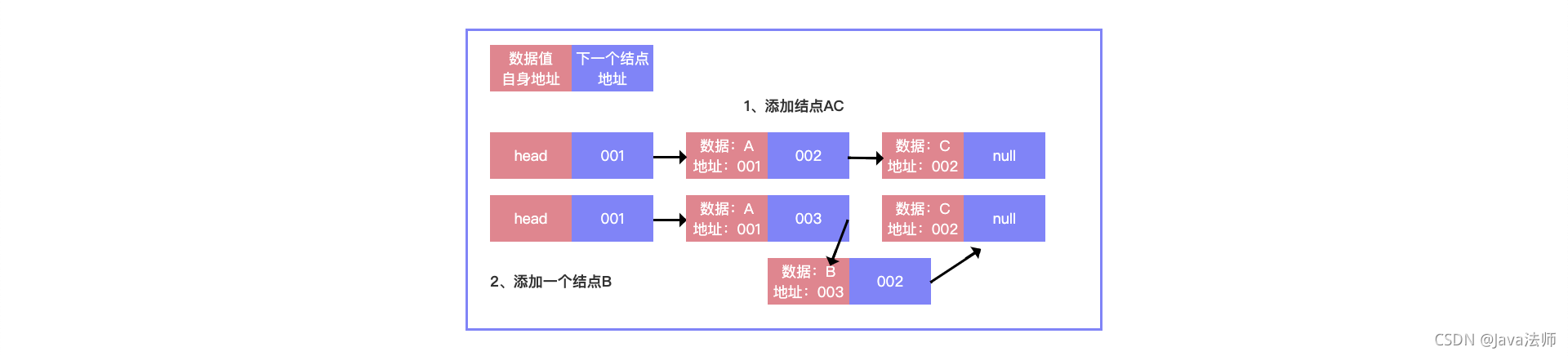
双向链表：

单向链表如果说是只能向右看，那么双向链表就是可以左右看了，它是前面记录上一个的地址，后面是下一个的地址。 一般用双向链表比较多，因为比较方便

总结：

链表元素不是连续存放的，上一个元素记录下一个元素的地址，查慢、增删快

二叉树：

• 二叉树是高度平衡的数据结构，误差超过1就会旋转
• 树的作用可以做排序可以做索引，比较方便，查找的时候呢可以说是（二分搜索）就是你每次找判断都砍掉一半无用的树
• 每个节点不超过2，左子树元素小，右子树元素大
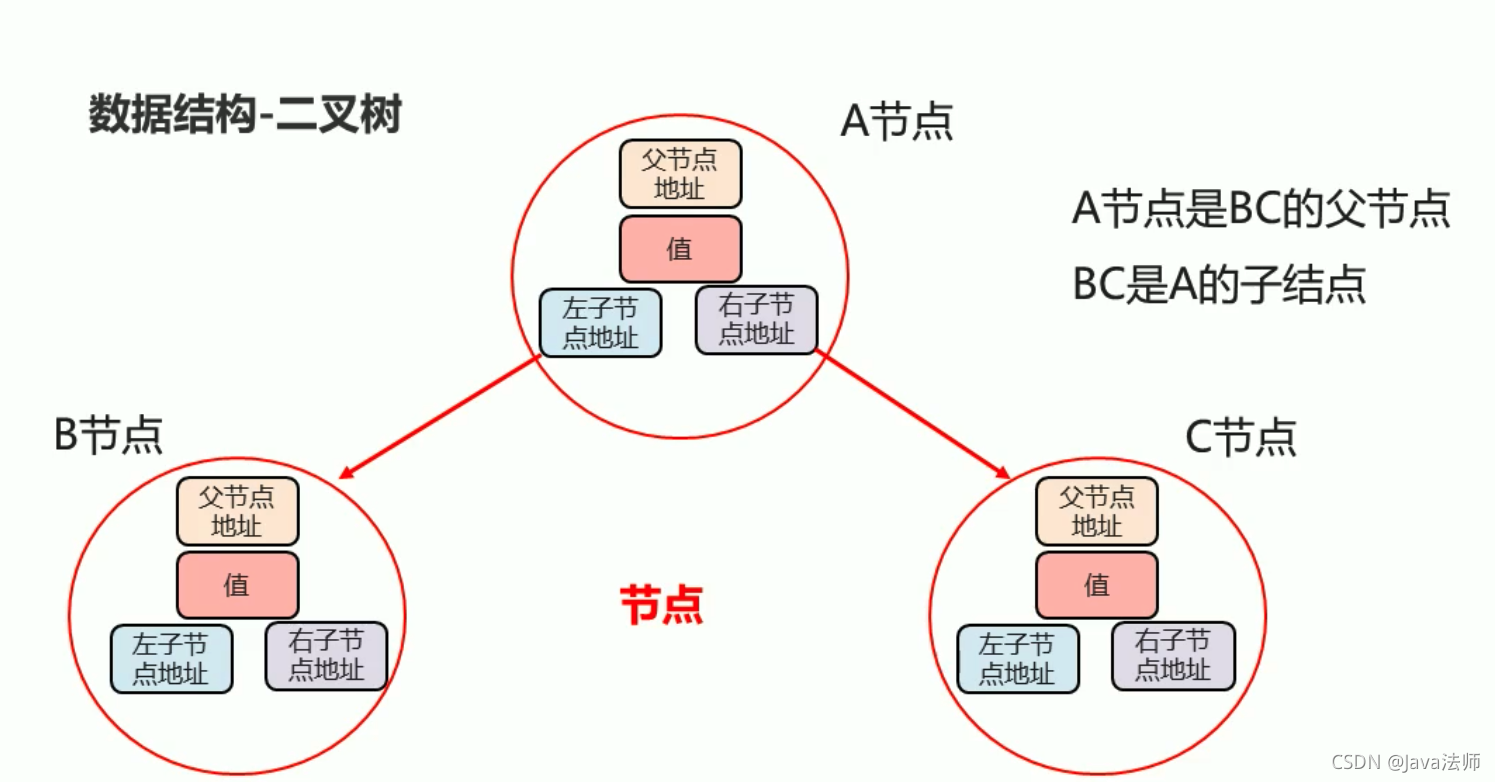
• 节点: 在树结构中,每一个元素称之为节点
• 度: 每一个节点的子节点数量称之为度

二叉树结构图：

二叉查找树：

二叉树和二叉查找树对比：

二叉树没有规律，而二叉查找树有规律，任意的一个结点都是左小右大

二叉查找树添加原理：

• 先和根节点比较，再和子节点比较，小存左、大存右、相同不存
• 拿数据7、4、10三个数据举栗
• 先存7作为根节点，再存4，存4的时候要判断4是大于7还是小于7，小于就做位7的左子节点，大于就做位7的右子节点。10也是一样。然后就是7为根节点，4为左子节点，10位右子节点。

二叉查找树的弊端：

• 拿数据7、10、11、12举栗
• 先存7作为根节点
• 再存10，存10的时候要判断4是大于7还是小于7，然后就成为了7的右子节点。
• 再存11，12，最后发现，整棵树都是右子节点，没有左子节点。
• 那么查找的时候就要一个一个的去遍历，效率低，因为左子节点和右子节点高度差太大。

平衡树二叉树：

• 二叉树左右两个子树的高度差不超过1
• 任意节点的左右两个子树都是一颗平衡二叉树
• 平衡二叉树存在的意义就是解决二叉树高度不一致的问题

旋转树：

• 旋转树就是平衡机制，存在就是保证二叉树的平衡
• 旋转触发时机： 只有平衡二叉树和红黑树会用到，当添加节点破坏了平衡就会触发左右旋转

左旋：

逆时针左旋转，整体往左旋转，右子节点变父节点，原来的根节点降级成左子节点，多余的左子节点给降级的左子节点当右子节点

右旋：

顺时针右旋转，整体往右旋转，左子节点变父节点，原来的根节点降级成右子节点，多余的右子节点给降级的右子节点当左子节点

平衡二叉树旋转的四种情况：

左左：

• 当根节点左子树的左子树有节点插入,导致二叉树不平衡
• 如何旋转: 直接对整体进行右旋即可
• 4会做为根节点，2为左子节点，7为右子节点，5为7的左子节点

左右：

• 当根节点左子树的右子树有节点插入,导致二叉树不平衡
• 如何旋转: 先在左子树对应的节点位置进行左旋,在对整体进行右旋
• 先把圈起来的部分左旋，然后如图二再右旋

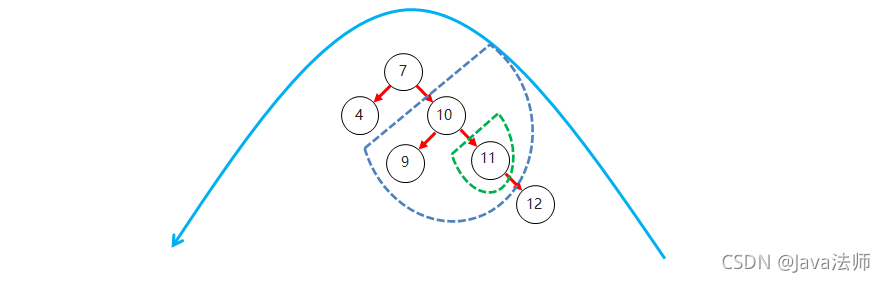
右右：

• 当根节点右子树的右子树有节点插入,导致二叉树不平衡
• 如何旋转: 直接对整体进行左旋即可
• 将10做为根节点，7成为10的左子，11为右子，9为7的右子节点

右左：

• 当根节点右子树的左子树有节点插入,导致二叉树不平衡
• 如何旋转: 先在右子树对应的节点位置进行右旋,在对整体进行左旋
• 先把10节点下的右旋，然后如右图所示再整体左旋

红黑树：

• 红黑树(平衡二叉B树）
• 每一个节点可以是红或者黑
• 红黑树不是高度平衡的,它的平衡是通过自己的"红黑规则"进行实现的

红黑规则：

1. 每一个节点或是红色的,或者是黑色的
2. 根节点必须是黑色
3. 如果一个节点没有子节点或者父节点,则该节点相应的指针属性值为Nil,这些Nil视为叶节点,每个叶节点(Nil)是黑色的
4. 如果某一个节点是红色,那么它的子节点必须是黑色(不能出现两个红色节点相连 的情况)
5. 对每一个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点

添加节点规则：

1. 添加节点的时候默认为红色效率高（对应红黑规则跳转比较少）
2. 红黑树添加节点后如何保持红黑规则
   如果是根节点位置，直接变为黑色
   非根节点位置，父节点为黑色，不需要任何操作,默认红色即可
3. 父节点为红色叔叔节点为红色
   将”父节点”设为黑色,将”叔叔节点”设为黑色
   将”祖父节点”设为红色
   如果”祖父节点”为根节点,则将根节点再次变成黑色
4. 叔叔节点为黑色
   将”父节点”设为黑色
   将”祖父节点”设为红色
   以”祖父节点”为支点进行旋转