水的渲染一直是图形学需要解决的问题，本篇博客主要介绍用傅里叶变换算法实现的水反射，也是一种假反射效果，目的是优化效率。实现的效果如下图所示：

使用傅里叶系数来表示地形高度的假反射效果，在我们开发的游戏中使用水着色器，告诉读者我将如何利用引擎处理水的反射，我们自己开发水渲染效果，需要在优化方面考虑，计算每帧渲染时间。我们要处理渲染简化的低分辨率反射地图，因为我们还要渲染对于流动的水平面。算法的实现其实都是源于生活，大家如果平时出去旅游，经常会看到山丘的反射，近处反射的比较清晰，但在远处它只是一个黑色的斑点。试想一下，如果我们能够记录每个水点周围的水面上方的地形的角度，然后我可以在水着色器中使用这个反射光线，它应该是从“天空”过渡到“地形”的点。(Spherical harmonics)球面谐波是一种众所周知的技术，通常用于全局照明。非常简要地总结：每个顶点存储一组预先计算的系数，这允许我们重建击中对象的环境光。这些系数基本上存储从每个方向照射该点的光的映射图。反射/环境光通常是非常低的频率，因此这是这些系数如何包含这么“多”的信息原因。我决定用我引擎中的水尝试类似的技术，每个顶点保存一组小系数，描述地形在水上方围绕该点的每个方向上升的角度。这可以用一个四元系列的系数来描述 - 基本上是球面谐波的2d方程。当在顶点之间插值时，这些傅里叶系数就可以计算出来了，给读者展示一下效果图吧。

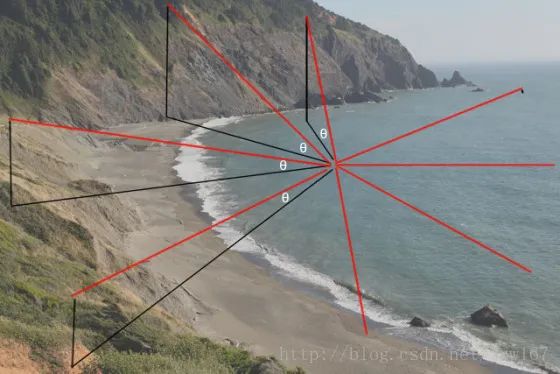
在水上的一个点周围的采样方向上的各种角度。

我们计算每个水顶点的系数，这涉及每个顶点的操作：

1、在点周围选择  k个均匀间隔的采样方向。k的值只影响计算，因此您可以将其设置为一定

的高以实现其仿真度，我目前使用13。

2、对于每个采样方向，执行光线跟踪。一次执行一个高度地图像素，测量水面上方的地形角度。你想要精确的反射取决于你离岸的距离，在本文的示例应用程序中，我目前使用5个像素。如果你的游戏涉及从低水平面的不同的水观察视角，你将需要使用更多(后面更多)。

3、现在我们有一个函数(每2π循环)表示点周围的地形高度。

4、为了获得表示该函数的傅里叶系数，我们需要对每个系数的表达式进行积分计算，确切的表达式可以在网上找到。我使用数值积分，分辨率为400(例如每个函数400个样本)，使用的数字仅影响计算。

 5、我计算前8个系数，这个数字直接影响效果的品质和性能。8对我的目的来说肯定够好了，当然我们会尽量降低。

我把我的系数作为16位浮点存储在我的顶点结构中(因此每个顶点占用16个字节)。

在水着色器中，我使用反射向量来确定我设置的角度，代码如下：

float3 reflectionRay = reflect(worldPosition - CameraPosition, normal);float angle = atan2(-reflectionRay.z, -reflectionRay.x) + PI;//这给出了0和2π之间的角度，然后我们能够使用它来查找地形高度。

本文实现的傅里叶评估函数看起来像这样(t是角度)：

float EvaluateFourier(float t, float4 coefs1, float4 coefs2){  float4 sins;  float4 coses;  sincos(float4(t, 2 * t, 3 * t, 4 * t), sins, coses);  float value = coefs1.r; // a0  value += coefs1.g * coses.r; // a1  value += coefs1.b * sins.r; // b1  value += coefs1.a * coses.g; // a2  value += coefs2.r * sins.g; // b2  value += coefs2.g * coses.b; // a3  value += coefs2.b * sins.b; // b3  value += coefs2.a * coses.a; // a4  return value;}

方程给了我一个角度，这也是算法与编程结合的函数实现，然后我可以比较水面上的反射光线的角度，以确认我们是否应该绘制天空或反射的地形，目前我只是使用黑色的反射地形，效果似乎满足需求。如果我们想要更好的效果，还可以存储地形的颜色，除了高度。当然这将使所需的数据量增加四倍。

那它是如何工作的呢？您可以查看本文顶部的照片作为示例。这里有一个版本的顶点网格绘制。每个顶点存储16字节的数据在我当前的实现。

上图显示了我使用的顶点分辨率效果。

在水面上使用的法线贴图有助于实现这种假反射效果，实现的效果如下所示：

以上实现的效果在性能方面也给读者分析一下，这也有助于读者优化Shader的渲染效果：上面给读者实现了一种假反射，以避免渲染昂贵的反射贴图，因此它需要具有高性能。不幸的是，这需要大量的着色器指令在我当前的实现中评估。atan2约有20条指令。HLSL产生4个标量sincos指令，其实际上每个占用8个指令槽。总共，它为像素着色器添加了约64个指令槽。针对上述问题，我们的下一步任务是找到一种减少指令数量的方法。可以使用atan，然后是正弦和余弦，我可以通过做一些三角取代来减少这一点。或者我可以考虑使用e与虚数的幂的和来评估该系列。当然我们还可以减少系数的数量。另外，我将看到我是否可以存储每个系数在单个字节而不是16位浮点。最后总结一下，对于具有更多不同视图的游戏，这可能不是一个很好的选择。还有这个技术的一个问题是它只反射静态对象，地形，以及你决定在你的射线检测算法中包含的任何其他游戏元素。