(西安市第八十六中学   刘丽丽)

       学科教学要注重知识的“生长点”和“延伸点”，把课时知识置于学科整体逻辑体系中，关注结构和通法，处理好局部与整体之间的关系。所以在北师大版八年级上册数学第一章《勾股定理》的备课中，我再次以问题导向为基础，从单元整体角度出发，依据教材把握教学内容的地位与作用，建构对勾股定理的整体认知，让学生真正经历知识的生成、生长，并体验相应的数学思想。

一、对勾股定理的单元整体思考

      勾股定理以“数与形的第一定理”著称，更是得到了古今中外无数学者的研究与证明，它刻画了直角三角形三边的数量关系，由“形”定“数”，体现了“数”与“形”的完美结合。勾股定理蕴含着丰富的历史文化内涵，它还推进了数的发展，它不仅在数学领域有重要地位，而且在其他学科领域中也被广泛应用。

      教材地位：在本单元之前，学生学习了三角形的相关知识，并从一般到特殊，认识了特殊的三角形——等腰三角形、直角三角形的有关性质，以及整式运算中的完全平方公式。在已有知识的基础上，根据特殊角与特殊边的联系探索直角三角形的另一条性质——勾股定理。勾股定理不仅刻画了直角三角形三边的数量关系，它还推进了无理数的发现。

     根据课标对勾股定理教学的要求，我确定本章的如下教学目标：

1、经历勾股定理的探索过程，感受勾股定理反映的直角三角形的三边之间的数量关系，从数的角度研究图形性质和运动，在探究过程中进一步发展学生的空间观念；

 2、体验勾股定理的验证过程，发展合情推理能力，渗透数形结合和从特殊到一般的数学思想；

 3、经历从不同角度分析问题和解决问题的过程，体验解决问题方法的多样性；

4、掌握直角三角形的性质和判定，以及勾股数的概念；辨析勾股定理及其逆定理之间的关系，并能用它们解决一些简单的实际问题。

二、对勾股定理的整体教学构思

1.知识过渡

       在七年级学生已经学习了最基础的平面几何图形——三角形，所以可以提取学生对三角形的认识，从角的角度谈一谈对三角形的认识、从边的角度谈一谈对三角形的认识，按照几何的研究顺序，从一般到特殊，我们有等腰三角形中特殊的角关系必然带来特殊的边的关系，思考直角三角形三边是否也存在特殊的关系，从而引入对《勾股定理》一章内容的探究。

设计目的：关注知识前后的关联，正确把握学情。带着问题引入，这样思维才有方向,有了问题,思维才有动力。

2.定理探究

      小组合作画出直角三角形，测量三边的长度，探究三边长是否存在一次关系。如果没有，那平方关系呢？并由的几何意义联想到借助正方形面积进行探究。

      再按照课本内容，学生通过面积的度量、数格子、拼图等多种方法，从特殊到一般发现、验证勾股定理，让学生经历勾股定理的生成过程。同时，在这一过程中，学生经历了思考、尝试、探索等过程，探究问题、解决问题、学习新知识，也加深了割补法求图形面积的数学方法，激发了学生的学习热情，并从中体会了数形结合的重要性，同时理解了数学知识的本质，从而提升数学素养。

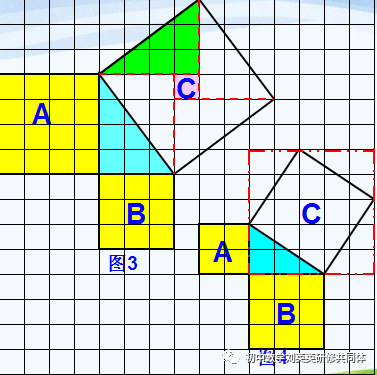
3.古今定理证明

     古今中外，勾股定理的证明方法中最多的就是面积变换法，当然这也是初中数学中要求学生掌握的一种数学素养，所以，我在教学中主要介绍了几种等面积证法。

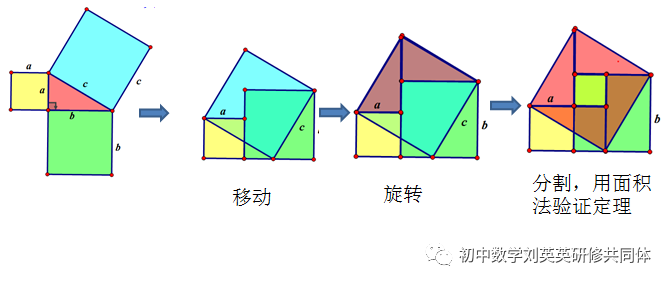
方法一：毕达哥拉斯证明勾股定理

方法二：赵爽弦图

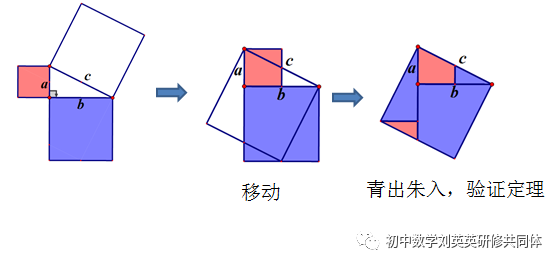
方法三：青朱出入图

     同时，教师在教学中可以介绍中外古代人们对勾股定理证明的研究，渗透数学史，数学史所展现的知识脉络不仅有助于教师对勾股定理的整体认识，理解知识及背后所涉及的思想与方法，关注知识、方法之间的内在联系，更可以激发学生对数学的钻研精神，通过对勾股定理历史的了解，感受数学文化，增强爱国情感。

4.逆定理的思考

      在此之前，学生在学习的过程中已经具备了一定的逆向思维的经验，所以学习了勾股定理后，可以引导学生逆向思维从而引出勾股定理的逆定理。该定理的验证过程学生可以通过测量、几何画板等形式得出，但还是缺少数学的严谨性，所以教师可以引导学生去推理说明，而反证的思路还需要教师适当的引导。

5．知识应用

     本章的应用主要有利用直角三角形的三边关系求边长、通过边判定直角三角形 形状、化曲为直求最短距离、利用方程思想解决折叠问题、面积问题等，教师可以以专题的形式进行讲解，增强学生的模型意识。

    比如：

[利用勾股定理求面积]

    以直角三角形的边a,b,c为边，向外做等边三角形，半圆，等腰直角三角形，正方形，上述四种情况的面积关系满足S1+S2=S3的图形个数为______。

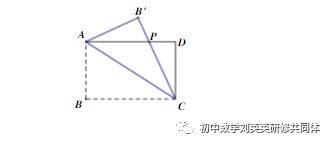
[折叠问题]

    如图，长方形ABCD中，AB=6，BC=8，沿着对角线折叠，使得点B落在B’处，求PD的长。

[利用勾股定理求最短路径]

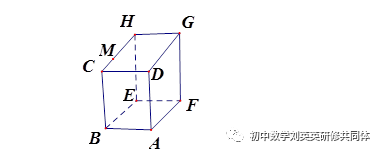
    如图，长方形的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上，且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M，需要爬行的最短距离是多少？

[勾股定理逆定理的应用]

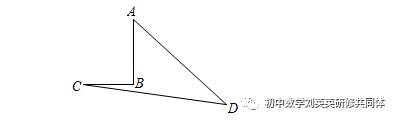
    如图，在四边形中，已知AB=12,BC=9,∠ABC=90°,且CD=39,DA=36．求四边形ABCD的面积．

[勾股定理的实际应用]

    同学们在测量学校旗杆的高度时发现：将旗杆顶端升旗用的绳子垂到地面还多2米；当把绳子的下端拉开8米后，下端刚好接触地面，如图，根据以上数据，同学们准确求出了旗杆的高度，你知道他们是如何计算出来的吗？

三、数学思考

      数学就像一个大铁链，环环相套，并不是孤立的。这要求老师要站在更高的角度，把一个学段作为一个整体，通盘考虑，规划整合，综合设计，有序实施，进行知识的有效迁移，重构符合教学实际的新知识系统，使教学环节更紧凑，更高效，所以吃透教材尤为重要。在教学中从单元整体出发，为知识自然生长埋种布线、有效备课、真正站在学生的角度去听、去理解问题；讲课的同时有效做到知识、方法、学科素养的渗透。努力通过具体知识的教学揭示其中的隐性知识——数学的本质、过程、思想和结构。

                              End

撰稿：刘丽丽

编辑：聂晓岐

      审核：刘英英