
难度:中等
题目:
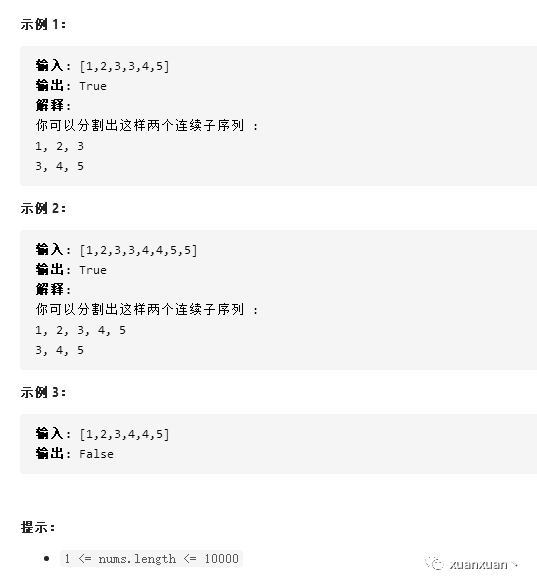
给你一个按升序排序的整数数组 num(可能包含重复数字),请你将它们分割成一个或多个长度为 3 的子序列,其中每个子序列都由连续整数组成。
如果可以完成上述分割,则返回 true ;否则,返回 false 。
------------------------------------------------------
思考:
题目要求,把数组分割成一或多个连续的子串,那就是要把尽可能多的数字弄成子串,看着有点像可以贪心。
如果用贪心的话,例如实例2,先尽可能多的从1开始把12345排成一个子序列,然后剩下345排成另一个子序列。
诶好像可以。
但是到了示例1这种就8行了。先拿出12345,然后就会只剩下3,不成立,但其实他却是成立的。
其实,上面解释这种只是普通的一般的贪心,我们可以改变一下,升级一下,非一般的贪心。
一个一个地贪心。
思路:
先用两个hashMap,一个countNum用来记录数字出现次数,一个tail记录以每个数字num结尾的子序列数。
然后遍历数组,从头开始,
先判断countNum的对应数字(例如X)数量是否>0,如果是则再去查找有没有以数字X-1为结尾的子X序列,有则把数字X续上,tail的X-1结尾的序列数量-1,X结尾的+1,countNum中的X数量-1。
继续判断下一位。
如果全部都能连上就是成功。否则有一个不能连上就是失败。
以示例1来说,
首先看1,先去countNum查找1的数量,如果>0个,则再去查找tail。如果有以1前一位(也就是0)结尾的,就在后面再续上,然后countNum的num的对应数量-1,tail的前一位的数量-1,1结尾的+1;如果tail没有以前一位结尾话,就去看后两位,2和3的countNum是不是同时>0,如果是则连成子串,对应的123的countNum-1,tail对应的3数量+1。
然后看2,因为上面123连成了,123都-1,countNum的2数量=0.
再看3,上面减了1,countNum的3数量为1,同样查找tail,没有以前一位(2)结尾的,直接查看后两位,有,连成子序列345,countNum各个数-1,tail为5的+1。
最后都可以连上,成功。
代码:
public boolean isPossible(int[] nums) { // 用一个哈希表统计每个数字出现的次数 Map countNum = new HashMap<>(); for (int num : nums) countNum.put(num, countNum.getOrDefault(num, 0) + 1); // 定义一个哈希表记录最长的子序列 Map tail = new HashMap<>(); for (int num : nums) { int count = countNum.getOrDefault(num, 0); if (count <= 0) {//当前元素已经用完,直接跳过 continue; } else if (tail.getOrDefault(num - 1, 0) > 0) {//前面还有数字,可以构成以num结尾的子序列 countNum.put(num, count - 1); tail.put(num - 1, tail.get(num - 1) - 1);//覆盖当前最长的子序列 tail.put(num, tail.getOrDefault(num, 0) + 1);//当前以num结尾的子序列+1 } else if (countNum.getOrDefault(num + 1, 0) > 0 && countNum.getOrDefault(num + 2, 0) > 0) {//前面无数字构成子序列后,判断能不能跟后面的构成子序列 countNum.put(num, count - 1); countNum.put(num + 1, countNum.get(num + 1) - 1); countNum.put(num + 2, countNum.get(num + 2) - 1); tail.put(num + 2, tail.getOrDefault(num + 2, 0) + 1);//当前以num+2结尾的子序列+1 } else return false;//前后不能构成子序列则不成立 } return true;}时间复杂度:两个独立的循环,一个记录各个数字个数,一个遍历数字情况。所以是O(n)
空间复杂度:两个独立的哈希表存储数字个数和子序列数,所以是O(n)
----------------------------------完--------------------------------
淦里良欸








——数据库的索引碎片、计划缓存、统计信息)





)




--特征提取--TF-IDF)