曼哈顿距离最小生成树与莫队算法（总结）

1 曼哈顿距离最小生成树

曼哈顿距离最小生成树问题可以简述如下：
给定二维平面上的N个点，在两点之间连边的代价为其曼哈顿距离，求使所有点连通的最小代价。
朴素的算法可以用O(N2)的Prim，或者处理出所有边做Kruskal，但在这里总边数有O(N2)条，所以Kruskal的复杂度变成了O(N2logN)。
但是事实上，真正有用的边远没有O(N2)条。我们考虑每个点会和其他一些什么样的点连边。可以得出这样一个结论，以一个点为原点建立直角坐标系，在每45度内只会向距离该点最近的一个点连边。
这个结论可以证明如下：假设我们以点A为原点建系，考虑在y轴向右45度区域内的任意两点B(x1,y1)和C(x2,y2)，不妨设|AB|≤|AC|（这里的距离为曼哈顿距离），如下图：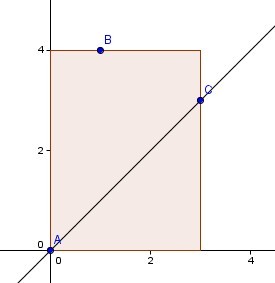

|AB|=x1+y1，|AC|=x2+y2，|BC|=|x1-x2|+|y1-y2|。而由于B和C都在y轴向右45度的区域内，有y-x>0且x>0。下面我们分情况讨论：
1. x1>x2且y1>y2。这与|AB|≤|AC|矛盾；
2. x1≤x2且y1>y2。此时|BC|=x2-x1+y1-y2，|AC|-|BC|=x2+y2-x2+x1-y1+y2=x1-y1+2*y2。由前面各种关系可得y1>y2>x2>x1。假设|AC|<|BC|即y1>2*y2+x1，那么|AB|=x1+y1>2*x1+2*y2，|AC|=x2+y2<2*y2<|AB|与前提矛盾，故|AC|≥|BC|；
3. x1>x2且y1≤y2。与2同理；
4. x1≤x2且y1≤y2。此时显然有|AB|+|BC|=|AC|，即有|AC|>|BC|。
综上有|AC|≥|BC|，也即在这个区域内只需选择距离A最近的点向A连边。
这种连边方式可以保证边数是O(N)的，那么如果能高效处理出这些边，就可以用Kruskal在O(NlogN)的时间内解决问题。下面我们就考虑怎样高效处理边。
我们只需考虑在一块区域内的点，其他区域内的点可以通过坐标变换“移动”到这个区域内。为了方便处理，我们考虑在y轴向右45度的区域。在某个点A(x0,y0)的这个区域内的点B(x1,y1)满足x1≥x0且y1-x1>y0-x0。这里对于边界我们只取一边，但是操作中两边都取也无所谓。那么|AB|=y1-y0+x1-x0=(x1+y1)-(x0+y0)。在A的区域内距离A最近的点也即满足条件的点中x+y最小的点。因此我们可以将所有点按x坐标排序，再按y-x离散，用线段树或者树状数组维护大于当前点的y-x的最小的x+y对应的点。时间复杂度O(NlogN)。
至于坐标变换，一个比较好处理的方法是第一次直接做；第二次沿直线y=x翻转，即交换x和y坐标；第三次沿直线x=0翻转，即将x坐标取相反数；第四次再沿直线y=x翻转。注意只需要做4次，因为边是双向的。
至此，整个问题就可以在O(NlogN)的复杂度内解决了。

2 莫队算法

据说这个算法是莫涛提出的（Orz！），但是在网上到处都搜不到相关资料，最后问pty才知道的。这个算法是用于处理一类不带修改的区间查询问题的离线算法，其核心在于利用曼哈顿距离最小生成树算法对区间处理顺序进行处理。比如下面这个例题（清橙A1206《小Z的袜子》，就是莫队出的题）：
给定一个长为N的序列，每个元素的值是其颜色。有M次询问，每次询问从一个区间中随机选取两个元素同色的概率。
一次询问[l,r]的答案即，其中是区间中第i中颜色的个数。显然暴力是O(NM)的，而且一般的区间问题的思路似乎不适用。
我们先考虑一个简化的问题：所有的查询区间的左端点都是1。那么我们可以按右端点排序，假设已经处理出了[1,r]的答案，考虑转移到[1,r+k]，即添加k个元素，这个可以在O(k)的复杂度内求出。那么处理所有区间的复杂度（不考虑排序）就是O(N)。
那么如果是从[l,r]转移到[l’,r’]呢？复杂度即O(|r’-r|+|l’-l|)，也即点(l,r)到点(l’,r’)的曼哈顿距离。那么如果将所有询问转化成二维平面中的点，求曼哈顿距离最小生成树，再按照生成树的顺序做，就可以最小化区间之间转移的复杂度。可以证明（我不会证……似乎莫队的论文里有），这样做的复杂度是O(N^1.5)的。问题也就得到了解决。

【BZOJ2038】小Z的袜子

传送门
写在前面：莫队竟如此暴力……
思路：当初我对这个题的第一感觉——这个区间问题可以用线段树或者树状数组？答案当然是不能，于是我就去简单学了下莫队算法。在我看来，莫队（分块版，不是二维曼哈顿距离什么什么最小生成树）就是分块排序优化暴力查找，减少查找区间之间的覆盖长度，从而优化时间复杂度，有一种说法很精彩

如果我们已知[l,r]的答案，能在O(1)时间得到[l+1,r]的答案以及[l,r-1]的答案，即可使用莫队算法。时间复杂度为O(n^1.5)。如果只能在logn的时间移动区间，则时间复杂度是O(n^1.5*log
n)。其实就是找一个数据结构支持插入、删除时维护当前答案。

这道题的话我们很容易用数组来实现，做到O(1)的从[l,r]转移到[l,r+1]与[l+1,r]。

那么莫队算法怎么做呢？以下都是在转移为O(1)的基础下讨论的时间复杂度。另外由于n与m同阶，就统一写n。
如果已知[l,r]的答案，要求[l’,r’]的答案，我们很容易通过|l – l’|+|r – r’|次转移内求得。

对于它的时间复杂度分析

将n个数分成sqrt(n)块。按区间排序，以左端点所在块内为第一关键字，右端点为第二关键字，进行排序，也就是以(pos [l]，r)排序
然后按这个排序直接暴力，复杂度分析是这样的：
1、i与i+1在同一块内，r单调递增，所以r是O(n)的。由于有n^0.5块,所以这一部分时间复杂度是n^1.5。
2、i与i+1跨越一块，r最多变化n，由于有n^0.5块，所以这一部分时间复杂度是n^1.5
3、i与i+1在同一块内时变化不超过n^0.5，跨越一块也不会超过n^0.5，忽略*2。由于有n个数，所以时间复杂度是n^1.5
于是就是O(n^1.5)了

这道题是比较模板的莫队分块了，对于一个区间询问[L,R]，我们要求的ans是

 1 #include"bits/stdc++.h"
 2 #define LL long long
 3 using namespace std;
 4 int n,m,last_l=1,last_r;
 5 LL ans,p;
 6 int color[50010],block[50010];
 7 LL sum[50010];
 8 struct os
 9 {
10     LL part,l,r,nume,deno;//nume指分子，deno指分母
11 }q[50010];
12 int cmp1(os xx,os yy)
13 {
14     if (block[xx.l]<block[yy.l]) return 1;
15     if (block[xx.l]>block[yy.l]) return 0;
16     return xx.r<yy.r;
17 }
18 int cmp2(os xx,os yy){return xx.part<yy.part;}
19 inline LL gcd(LL x,LL y)
20 {
21     if (!y) return x;
22     return gcd(y,x%y);
23 }
24 main()
25 {
26     scanf("%d%d",&n,&m);
27     for (int i=1;i<=n;i++) scanf("%d",&color[i]);
28     block[0]=sqrt(n);
29     for (int i=1;i<=n;i++)
30     block[i]=(i-1)/block[0]+1;
31     for (int i=1;i<=m;i++)
32     scanf("%d%d",&q[i].l,&q[i].r),
33     q[i].part=i;
34     sort(q+1,q+m+1,cmp1);   
35 
36     for (int i=1;i<=m;i++)
37     {
38         q[i].deno=(q[i].r-q[i].l+1)*(q[i].r-q[i].l);
39         if (last_r<q[i].r)
40         {
41             for (int j=last_r+1;j<=q[i].r;j++)
42             ans+=((sum[color[j]]<<1)+1),
43             sum[color[j]]++;
44         }
45         if (last_r>q[i].r)
46         {
47             for (int j=last_r;j>q[i].r;j--)
48             ans-=((sum[color[j]]<<1)-1),
49             sum[color[j]]--;
50         }
51         if (last_l>q[i].l)
52         {
53             for (int j=last_l-1;j>=q[i].l;j--)
54             ans+=((sum[color[j]]<<1)+1),
55             sum[color[j]]++;
56         }
57         if (last_l<q[i].l)
58         {
59             for (int j=last_l;j<q[i].l;j++)
60             ans-=((sum[color[j]]<<1)-1),
61             sum[color[j]]--;
62         }
63         q[i].nume=ans-(q[i].r-q[i].l+1);
64         last_l=q[i].l;
65         last_r=q[i].r;
66     }
67     sort(q+1,q+m+1,cmp2);
68     for (int i=1;i<=m;i++)
69     {
70         if (!q[i].nume){printf("0/1\n");continue;}
71         p=gcd(q[i].nume,q[i].deno);
72         printf("%lld/%lld\n",q[i].nume/p,q[i].deno/p);
73     }
74 }