原标题：教程 | 用人工蜂群算法求解k-分区聚类问题

选自towarddatascience

作者：Pedro Buarque

参与：Pedro、刘晓坤

群体智能算法是一类受生物群体智能行为的启发而发展出来的算法，社会性动物例如蚂蚁、蜜蜂、鱼等，个体的简单、非直接目标指向的行为常常能在群体层面上涌现出惊人的高效实现目标的模式。本文介绍了如何使用人工蜂群算法(ABC)算法实现真实数据的聚类。

我之前的文章介绍了如何利用名为人工蜂群算法(ABC)的集群智能(SI)算法来解决现实世界的优化问题：https://medium.com/cesar-update/a-swarm-intelligence-approach-to-optimization-problems-using-the-artificial-bee-colony-abc-5d4c0302aaa4

这篇文章将会介绍如何处理真实数据、如何使用 ABC 算法实现聚类。在此之前，我们先了解一下聚类问题。

聚类问题

聚类问题是一类 NP-hard 问题，其基本思想是发现数据中的隐藏模式。聚类没有正式的定义，但它与元素分组的思想有关：通过分组我们可以区分元素为不同的组。

不同的算法族以不同的方式定义聚类问题。一种常见的经典聚类方法如下：它将问题简化为一个数学问题，即找到原始数据的一个 k 分区。

找到集合 S 的 k 分区等价于找到 S 的 k 个子集，其遵循以下两个规则：

1. 不同子集的交集等于空集。

2.k 个子集的并集为 S。

在分区聚类过程结束时，我们希望找到原始数据集的一组子集，使得一个实例只属于一个子集。具体如下图所示：

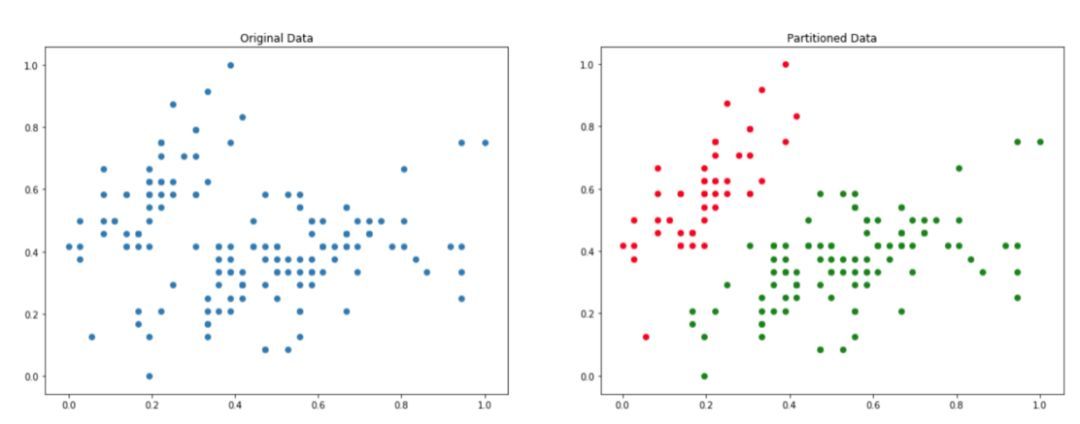
左边是原始数据，右边是 k=2 分区处理后的数据。

如何划分数据以达到上图所示的分区效果？聚类过程的输出是一组质心。质心是每个分组的代表实体，所以如果数据有 k 个分区，那么它有 k 个质心。

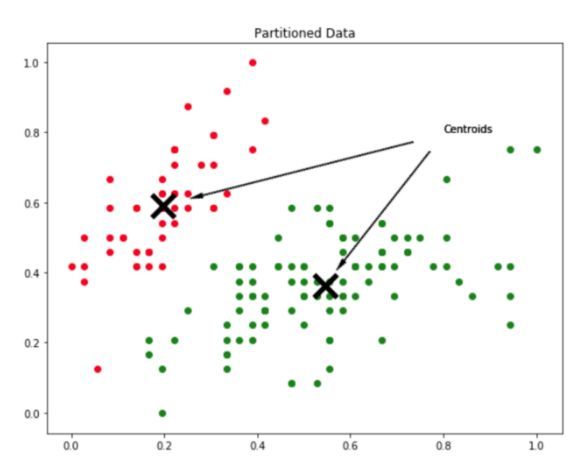
k=2 数据分区的质心演示示例。

质心也可理解为由数据定义的搜索空间上的点，由于每个质心定义了一个分组，每个数据点将被分配到距离它最近的质心。

人工蜂群算法的聚类应用

如何修改原始的 ABC 算法使其得以执行聚类任务？实际上，此处 ABC 算法没作任何改动。唯一要做的就是将聚类问题转化为优化问题。如何做到这一点？

一个明确定义的优化问题需要一个搜索空间：一组 d 维决策变量输入和一个目标函数。如果将人工集群中的每一个点(蜂)视为聚类问题的一个划分，那么每一个点可以代表一整组候选质心。如果对 d 维空间上的数据集执行 k 分区，那么每个点都将是一个 k·d 维向量。

上文定义了如何表示输入决策变量，接下来只需要弄清楚如何定义搜索空间的边界以及选用什么目标函数。

搜索空间边界的定义很容易，用 [0，1] 区间对整个数据集进行归一化，并将目标函数的值域定义为 0 到 1。麻烦的是如何定义目标函数。

分区聚类方法希望最大化两个不同组之间的距离，并最小化组内的距离。文献中提到了几个目标函数，但是最为人熟知的方法是所谓的平方误差和(Sum of Squared Errors，SSE)。

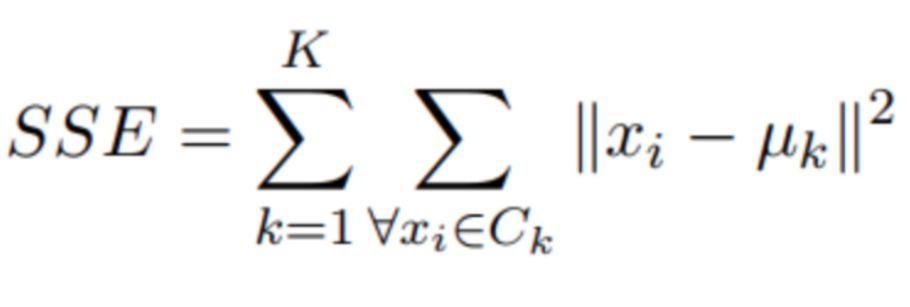
平方误差和的公式。

这个公式是什么意思？平方误差和(SSE)是一种聚类度量指标，其思想非常简单。它是一个计算数据中每个实例到其最接近质心的平方距离的值。算法优化的目标是尽量减小这个值的大小。

可以使用之前的目标函数框架来实现平方误差和，具体如下：

@add_metaclass(ABCMeta)

classPartitionalClusteringObjectiveFunction(ObjectiveFunction):

def__init__(self, dim, n_clusters, data):

super(PartitionalClusteringObjectiveFunction, self)

.__init__( 'PartitionalClusteringObjectiveFunction', dim, 0.0, 1.0)

self.n_clusters = n_clusters

self.centroids = {}

self.data = data

defdecode(self, x):

centroids = x.reshape(self.n_clusters, self.dim)

self.centroids = dict(enumerate(centroids))

@abstractmethod

defevaluate(self, x):

pass

classSumOfSquaredErrors(PartitionalClusteringObjectiveFunction):

def__init__(self, dim, n_clusters, data):

super(SumOfSquaredErrors, self).__init__(dim, n_clusters, data)

self.name = 'SumOfSquaredErrors'

defevaluate(self, x):

self.decode(x)

clusters = {key: [] forkey inself.centroids.keys()}

forinstance inself.data:

distances = [np.linalg.norm(self.centroids[idx] - instance)

foridx inself.centroids]

clusters[np.argmin(distances)].append(instance)

sum_of_squared_errors = 0.0

foridx inself.centroids:

distances = [np.linalg.norm(self.centroids[idx] - instance)

forinstance inclusters[idx]]

sum_of_squared_errors += sum(np.power(distances, 2))

returnsum_of_squared_errors

处理真实数据

现在开始尝试处理一些真实的数据，并测试 ABC 算法处理聚类问题的能力。此处我们使用著名的 Iris 数据集进行测试。

初始的四维数据集包含了从三种植物身上提取得到的特征。为了便于可视化，此处只使用该数据集的两个维度。观察该数据集第二维和第四维之间的关系：

importmatplotlib.pyplot asplt

fromabc importABC

fromobjection_function importSumOfSquaredErrors

fromsklearn.datasets importload_iris

fromsklearn.preprocessing importMinMaxScaler

data = MinMaxScaler().fit_transform(load_iris()[ 'data'][:, [ 1, 3]])

plt.figure(figsize=( 9, 8))

plt.scatter(data[:, 0], data[:, 1], s= 50, edgecolor= 'w', alpha= 0.5)

plt.title( 'Original Data')

上述代码的输出结果如下：

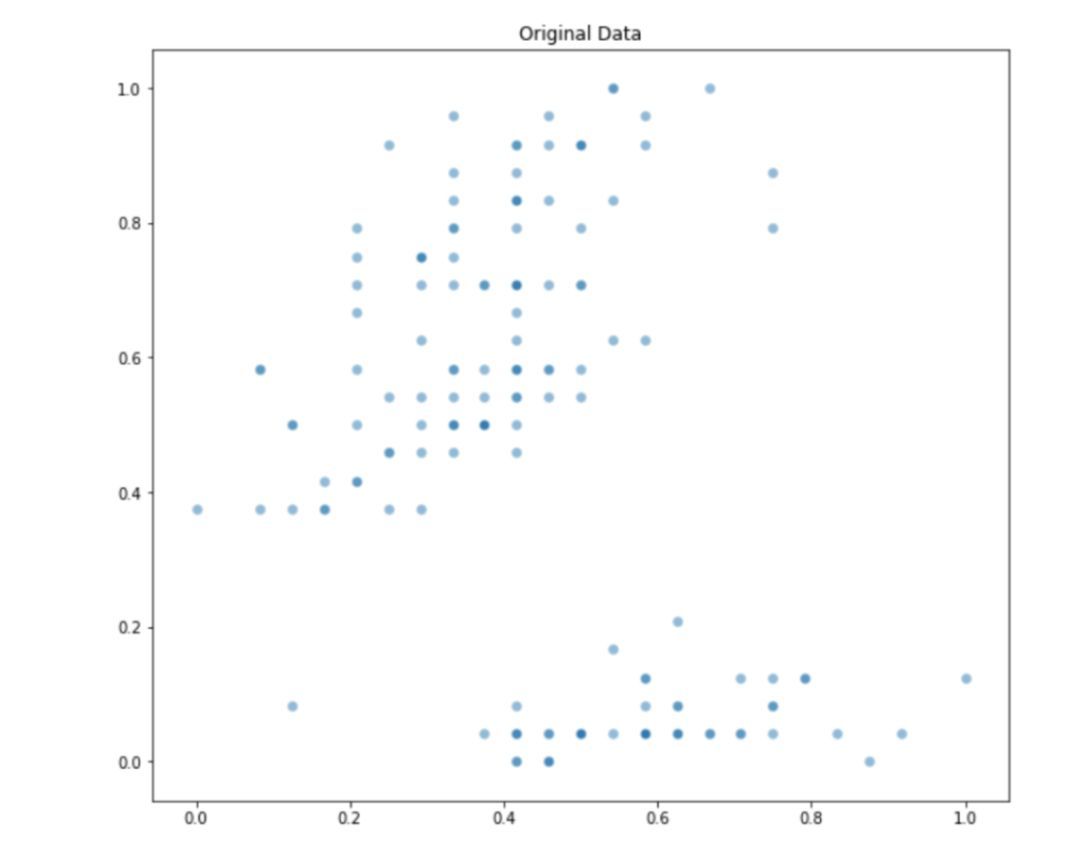
原始数据分布。

由于使用这些数据作为基准进行测试，因此其最佳划分已知，它是由这三种花的原始分布给出的。我们可以用下面的 Python 代码可视化 Iris 数据集的原始优化分区：

colors = [ 'r', 'g', 'y']

target = load_iris()[ 'target']

plt.figure(figsize=( 9, 8))

forinstance, tgt inzip(data, target):

plt.scatter(instance[ 0], instance[ 1], s= 50,

edgecolor= 'w', alpha= 0.5, color=colors[tgt])

plt.title( 'Original Groups')

它显示了如下分布：

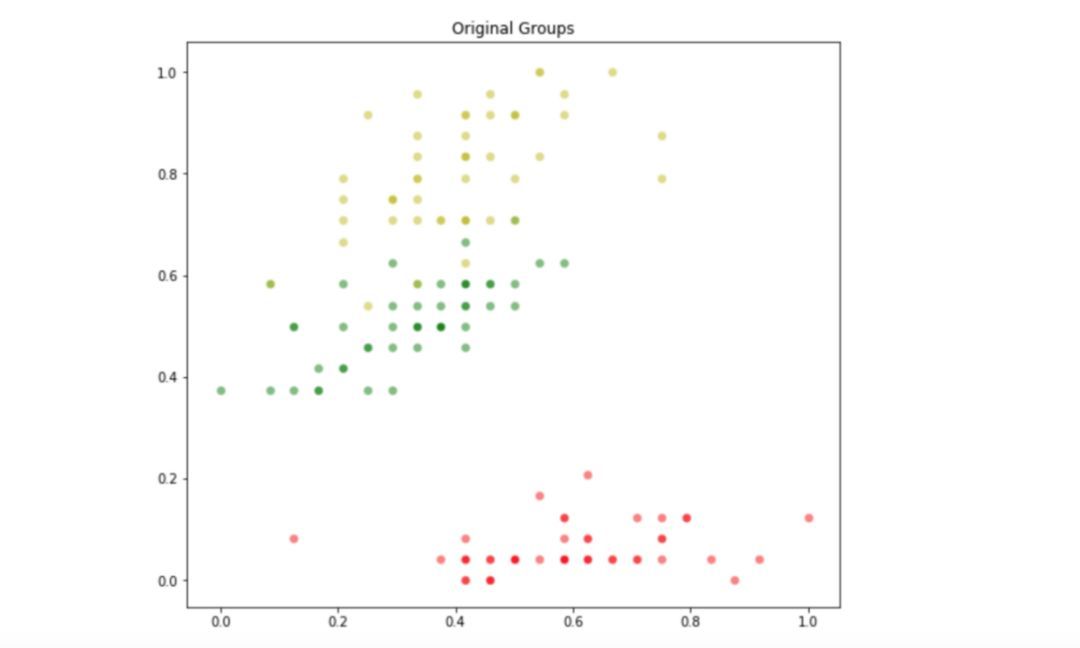
数据集的初始划分。

由于已经知道这个样本数据的原始最优分区是什么，接下来的实验将测试 ABC 算法能否找到一个接近最优解的解决方案。使用平方误差和作为目标函数，并将分区数设置为 3。

由于随机初始化，生成的质心的顺序可能与类的顺序不匹配。因此在 ABC 算法的输出图像中，组的颜色可能会不匹配。不过这并不重要，因为人们更关心的是对应分组的外观。

objective_function = SumOfSquaredErrors(dim= 6, n_clusters= 3, data=data)

optimizer = ABC(obj_function=objective_function, colony_size= 30,

n_iter= 300, max_trials= 100)

optimizer.optimize()

defdecode_centroids(centroids, n_clusters, data):

returncentroids.reshape(n_clusters, data.shape[ 1])

centroids = dict(enumerate(decode_centroids(optimizer.optimal_solution.pos,

n_clusters= 3, data=data)))

defassign_centroid(centroids, point):

distances = [np.linalg.norm(point - centroids[idx]) foridx incentroids]

returnnp.argmin(distances)

custom_tgt = []

forinstance indata:

custom_tgt.append(assign_centroid(centroids, instance))

colors = [ 'r', 'g', 'y']

plt.figure(figsize=( 9, 8))

forinstance, tgt inzip(data, custom_tgt):

plt.scatter(instance[ 0], instance[ 1], s= 50, edgecolor= 'w',

alpha= 0.5, color=colors[tgt])

forcentroid incentroids:

plt.scatter(centroids[centroid][ 0], centroids[centroid][ 1],

color= 'k', marker= 'x', lw= 5, s= 500)

plt.title( 'Partitioned Data found by ABC')

代码的输出如下：

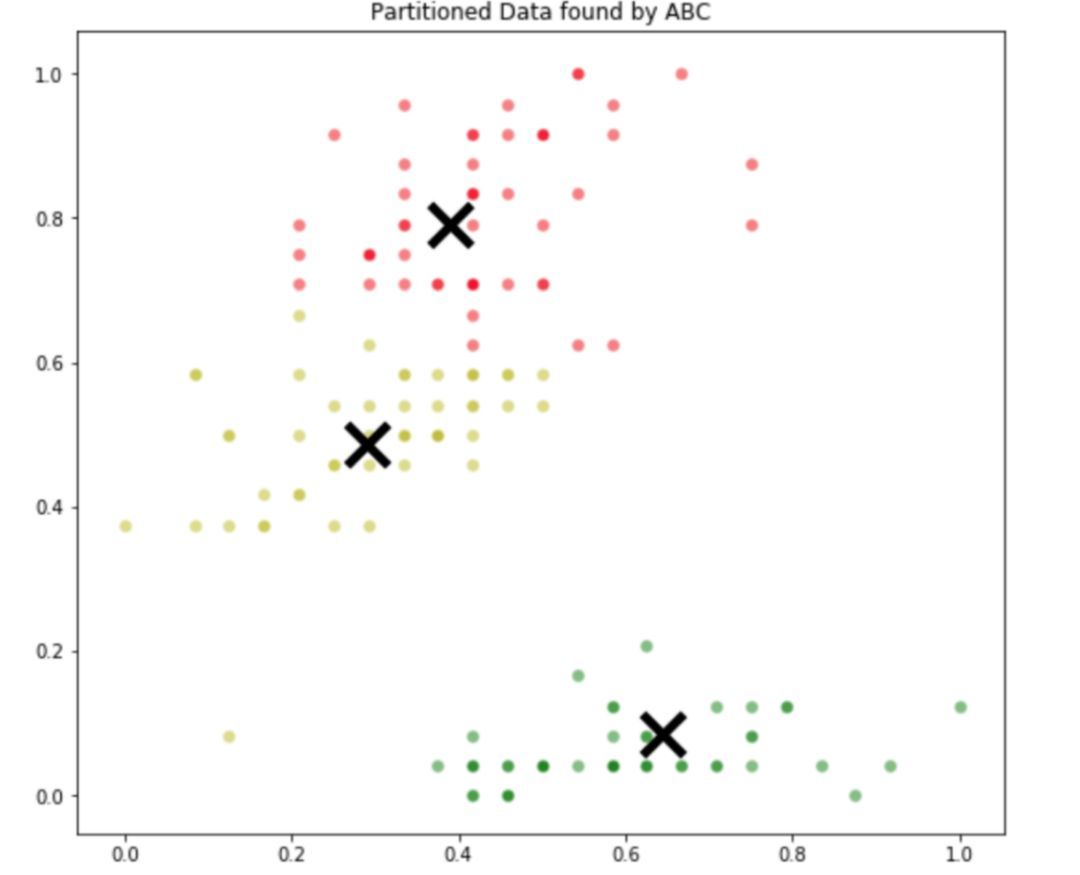
ABC 算法生成的分区

仔细观察原始分区和 ABC 算法生成的分区，可以看到 ABC 算法能够找到一个十分接近最优解的分区方法。这证明了用于聚类的 ABC 算法到底有多强大。还可以查看 ABC 算法的优化曲线来看看优化过程是如何进行的：

itr = range(len(optimizer.optimality_tracking))

val = optimizer.optimality_tracking

plt.figure(figsize=( 10, 9))

plt.plot(itr, val)

plt.title( 'Sum of Squared Errors')

plt.ylabel( 'Fitness')

plt.xlabel( 'Iteration')

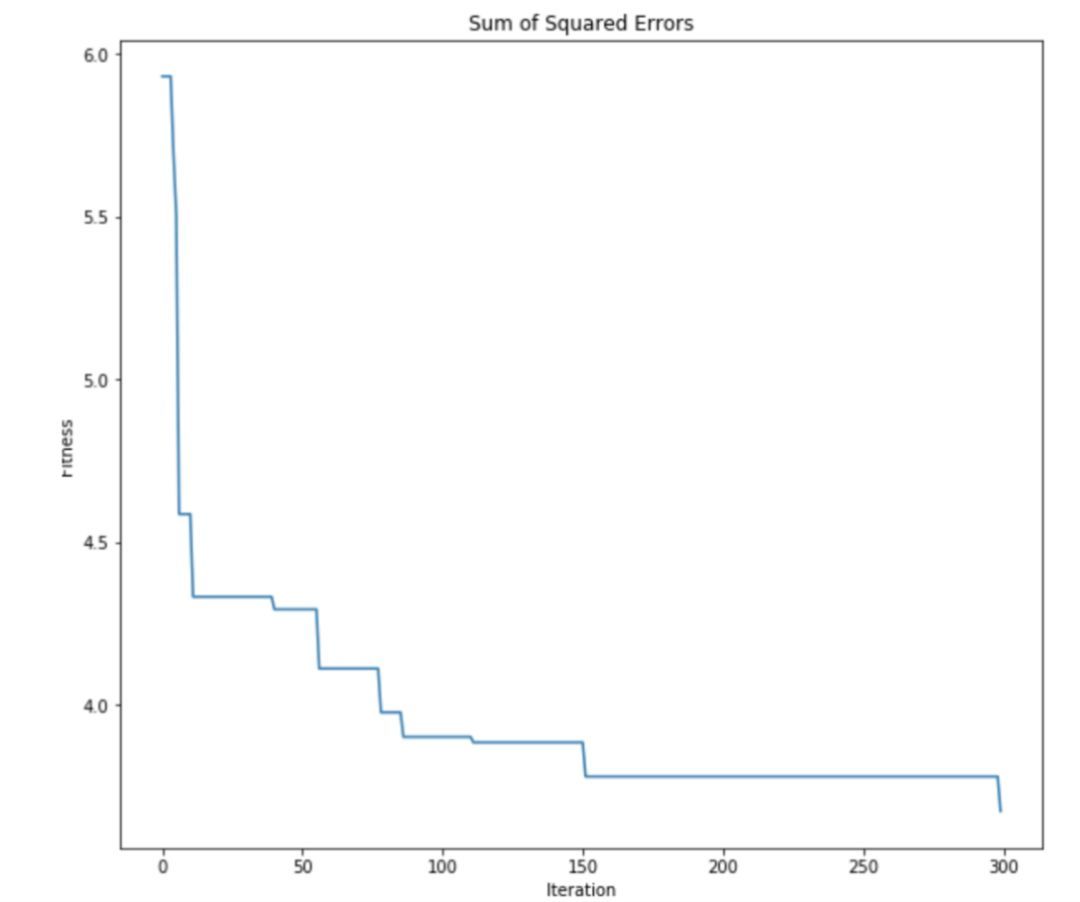
正如所料，ABC 算法能有效地最小化 SSE 目标函数。可以看到，集群智能拥有一些强大的机制来处理优化问题。只要能将现实世界的问题简化为优化问题，就能很好地利用这些算法。

参考文献：

A novel clustering approach: Artificial Bee Colony (ABC) algorithm—Dervis Karaboga, Celal Ozturk

A Clustering Approach Using Cooperative Artificial Bee Colony Algorithm—Wenping Zou, Yunlong Zhu, Hanning Chen, and Xin Sui

A Review on Artificial Bee Colony Algorithms and Their Applications to Data Clustering—Ajit Kumar , Dharmender Kumar , S. K. Jarial

A two-step artificial bee colony algorithm for clustering—Yugal Kumar, G. Sahoo

未来展望

本文通过实现人工蜂群算法简要介绍了集群智能，以及如何利用它来解决一些有趣的问题：例如优化实际函数、修改 ABC 算法解决聚类问题。

这些算法有很多应用，如图像分割、人工神经网络训练、数字图像处理和模式识别、蛋白质结构预测等等。还有一些其他强大的群体智能(SI)算法，如粒子群优化(PSO)和鱼群搜索(FSS)等，它们也是非常有名的技术，并且也有一些有趣的应用。

原文链接：https://towardsdatascience.com/a-modified-artificial-bee-colony-algorithm-to-solve-clustering-problems-fc0b69bd0788

本文为机器之心编译，转载请联系本公众号获得授权。返回搜狐，查看更多

责任编辑：