p-value

p-value

　　p-value翻译为假定值，假设几率。我们在生物信息中通常使用p值方法（P-Value, Probability, Pr）来做检验。那么p-value是什么呢？其实P-value就是一种概率，表示在原假设为真的前提下出现观察样本以及更极端情况的概率。

　　什么叫“更极端”情况呢，在此我们借用（https://blog.csdn.net/rongbaohan/article/details/53521147）举的抛硬币的例子，我们要检验一枚硬币是否质地均匀，现在我们假设这枚硬币质地是均匀的。那如何检验我们的假设呢？我们知道抛一枚质地均匀的硬币，正面和反面出现的概率均为0.5。那么我们就开始做实验：抛这枚硬币100次，假如我们观察到的结果是正面出现90次，反面出现10次，这个结果已经很不可能发生了，也就是极端情况了（质地均匀的硬币观察的应该是正反面出现次数均为50左右），那么所谓“更极端”的情况就是出现正面91次，反面9次，以此类推。为什么要去找“更极端”的情况呢？因为一个事件很极端，那么比它“更极端”的事件就非常少。

　　我们观察的结果（正面90次，反面10次）是在一次实验中得出的。我们重复做这个实验100次，每次抛100回硬币，现在要来考察“更极端”事件出现的概率。P-value=P(出现“更极端”情况的次数)，如果这个p-value < 显著性水平α，则说明在原假设为真的情况下出现事件（正面90次，反面10次）是极端的，以至于我们不再相信原假设，因为p-value很小就说明在原假设为真的情况下出现观察到的极端情况的概率很低，但是根据小概率事件原理，概率很低的情况在一次实验中不可能出现，而极端情况却出现了，所以我们拒绝原假设。

 

p-value有什么意义呢？

　　我们如果计算出的p-value很小，说明原假设情况发生的概率很小，而如果出现了，根据小概率原理，我们就有理由拒绝原假设，p-value越小，我们拒绝原假设的理由越充分。

　　另外，p-value越小，表明结果越显著。但是检验的结果究竟第“显著的”、“中度显著的”还是“高度显著的”，需要我们自己根据p-value的大小和实际问题来解决。

 

　　我们再举一个生物信息上的例子，现在要在人类21号染色体上找图a这样的模式序列，我们将这种模式序列称为motif。（来源Noble W S. How does multiple testing correction work?[J]. Nature Biotechnology, 2009, 27(12):1135-7.）

 

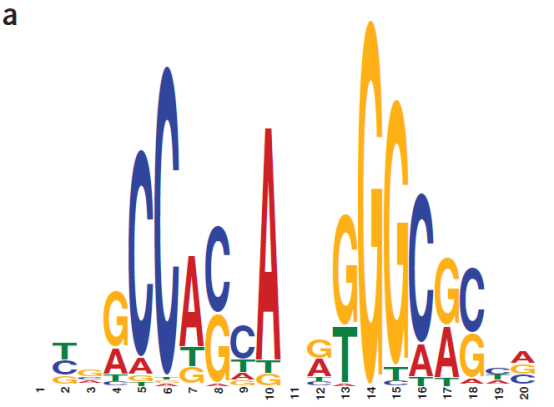
　　该motif一共由20个碱基组成，碱基有四种（A, T, G, C），其中每一列上字母的大小表示出现的可能性大小，比如说第6个碱基，明显“C”最大，那么该位置是“C”的可能性就越高。

　　我们在人类21号染色体上找到6800万个长度为20个碱基的序列，我们给每个序列一个score，表示该序列与motif的相似性，score值越大表明该序列越可能是我们要找的motif序列。我们打完分数，列出score值最大的20个序列（我们将这20个序列集合设为A）。现在要表明我们的方法计算出的这前20个序列是有意义的，就要评估这种情况偶然发生的可能性。

　　下图为前20个得分最高的序列，我们只关注score。其中最高的分数为26.30.

 

 

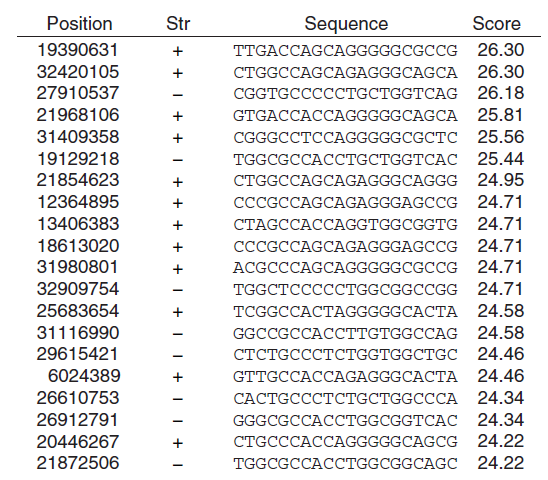
　　我们提出零假设：前20个序列是随机出现的。相应地，备择假设：前20个序列不是随机出现的，而是与我们的方法有关（备择假设的意义为：我们的方法是可行的，通过我们给出的方法找出前20个序列是有意义的）。

　　现在我们将21号染色体上的碱基顺序打乱，根据零假设，高分数是随机的，所以我们的方法对于顺序打乱的序列依然会得到很高的分数。我们记打乱顺序后找到的分数最高的20个序列的集合为B。通过相同的方法计算出的结果显示：在B集合中只有1个得分≥26.30，即分数为26.30的序列的p-value = 1/(6800万)=1.5*10^-8（找比26.30这个分数更极端的分数），如果设显著性水平为0.05，那么p-value << 0.05，即在原假设成立的情况下，出现26.30这样的高分数的概率非常非常小，也就是说我们得到的结果对原假设的支持程度非常非常小，所以我们拒绝原假设。

　　我们需要注意的是，p-value不是给定样本结果时原假设为真的概率，而是给定原假设为真时样本结果出现的概率。

　　所以我们的结果并不是在随机情况下出现的，说明我们的方法是有意义的，可以发现那些与motif相似性很高的序列。如果在碱基顺序打乱后，我们依然可以得到很多分数很高的序列，那么就表明我们的方法没有什么用，进而说明我们发现的那些分数很高的序列没有什么意义，那么我们做的这种研究就没有用了。

　　从假设检验上说，我们做研究时，并不希望得到的结果否定自己的假设，但是又无法完全证明得到的结果正确，所以我们通过建立一个与研究假设相反的假设H₀，利用假设检验来证明否定H₀，那么我们研究的假设相对来说就得到了接受。