参考图论算法（二）-最短路径的Dijkstra [ 单源 ] 和Floyd[ 多源 ] 解法（JAVA ）
这种算法也叫Floyd-Warshell算法，虽然和Warshell算法名字相近，算法思想也相近，但确实是两种算法。
对于一个带权图（无向或有向），全源最短路径问题就是找出每个顶点到其他所有顶点之间的最短距离。我们用一个n阶距离矩阵来记录最短路径的长度。需要注意的是该算法不适合带负权的回路图。
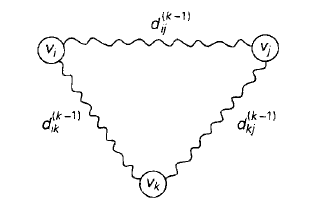
那么对于任意i到j的路径可以表示为：vi, 顶点标号不大于k的一个中间顶点集，vj
我们在把这种路径分成两个不相交的情况，
情况一：子集中不将第k个顶点作为中间顶点。在这种情况下，路径所包含的中间顶点的编号都不大于k-1；
情况二：子集中不将第k个顶点作为中间顶点。在这种情况下，顶点vk在中间顶点中，且出现过一次。
上述两种情况可以由下图表示：
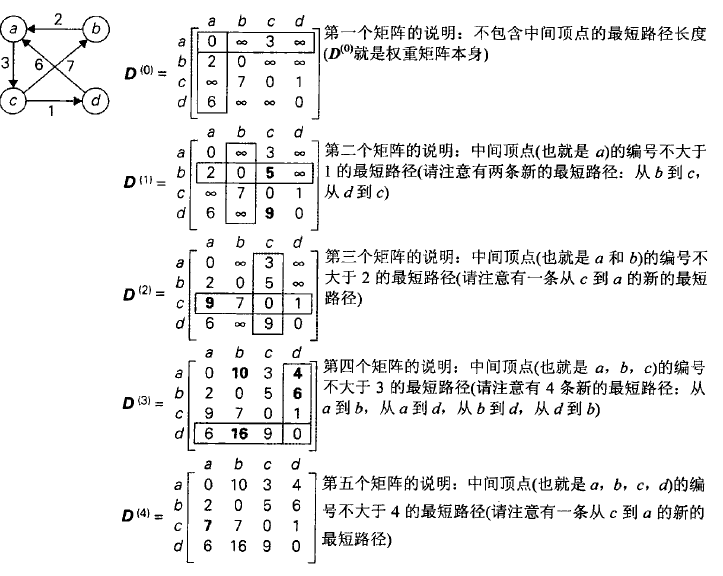
下面是一个实例用来展示算法的过程：
Input:
4 5
1 3 3
2 1 2
3 2 7
4 1 6
3 4 1
Output:
0 10 3 4
2 0 5 6
7 7 0 1
6 16 9 0
完整代码如下：
import java.util.Scanner;public class minPath {static int[][] e = new int[10][10];static int n, m;static Scanner input = new Scanner(System.in);public static void main(String[] args) {n = input.nextInt();m = input.nextInt();for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (i == j) {e[i][j] = 0;} else {e[i][j] = 99999999;}}}for (int i = 1; i <= m; i++) {int a = input.nextInt();int b = input.nextInt();int c = input.nextInt();e[a][b] = c;}floyd();for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {System.out.print(e[i][j] + " ");}System.out.println();}}public static void floyd() {for (int k = 1; k <= n; k++) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (e[i][j] > e[i][k] + e[k][j]) {e[i][j] = e[i][k] + e[k][j];}}}}}
}
