Fiddler响应拦截数据篡改，实现特殊场景深度测试（一）

利用Fiddler抓包调试工具，实现mock数据特殊场景深度测试（二）

利用Fiddler抓包调试工具，实现神奇特殊场景深度测试（三）

Fiddler抓包神器带你遨游网络，叱咤风云，为所欲为

Fiddler抓取APP请求（环境搭建）之mama再也不用担心抓不到包了

       最近我们上线了导入系统通讯录功能，有业务人员反馈在使用导入系统通讯录功能时，页面一直处于加载中，无法正常导入。

      我们进行问题重现定位，尝试了几个手机的导入功能都可正常使用，于业务人员手机对比找区别点，原来业务人员通讯录手机号比较多1000+左右，于是我们猜测可能是数据量大时导致的问题，尝试使用业务人员手机进行抓包定位，确认当通讯录手机号过多时接口异常，页面一直显示加载中，于是反馈给开发人员进行修复。

       这时我们经过回顾反思，确认当时测试时存在遗漏点，未考虑边界上限，也可能考虑了，估计因为觉得大量通讯录测试数据的难点就忽略测试了，我们得到教训，需求需要定义上下限，测试分析也需要考虑上下限，任何功能模块都需要考虑边界下限和边界上限进行测试，不能因为麻烦或疑难阻碍就抱着侥幸心理忽略掉，同时也应证了测试理论中的边界值测试法，定义测试标准是有它的道理的，永远无法脱离基准的。

         当初遇到的难点是大量通讯录数据，无法模拟的问题，没有1000+通讯录的手机，也不可能手动添加1000+个。

         经过一段时间的摸索，找到了一个很好的测试方法，借助Fiddler工具拦截请求，模拟大量数据5000+手机号，篡改请求数据，释放请求，达到要实现的测试效果。

开发修复完BUG后，我们进行回归验证测试

使用任意数量通讯录的手机，操作通讯录导入进行抓包。

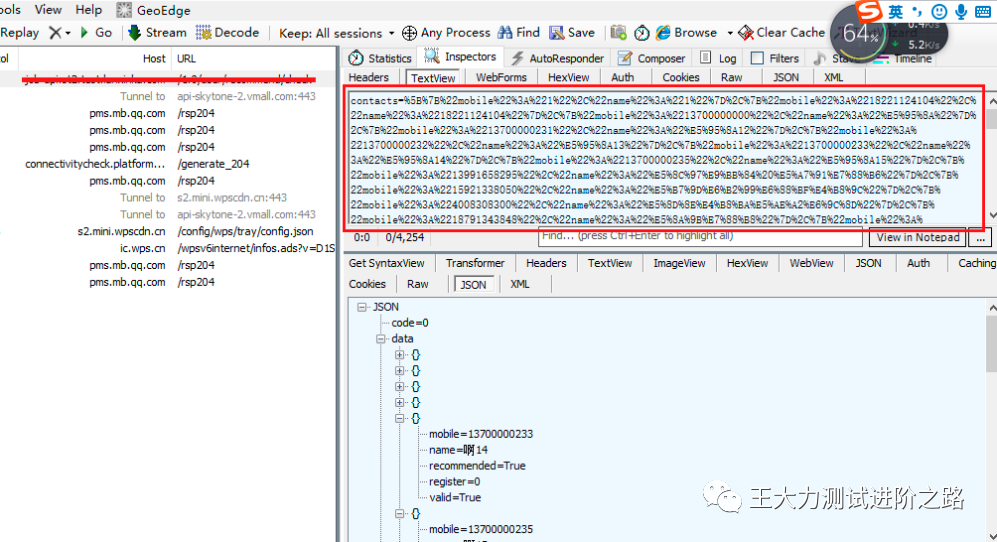
复制抓报的请求参数进行解码，这时我们可以看明白请求参数

将解码的参数粘贴到txt文件里，重复粘贴参数至5000+

 复制参数编码成能识别的参数

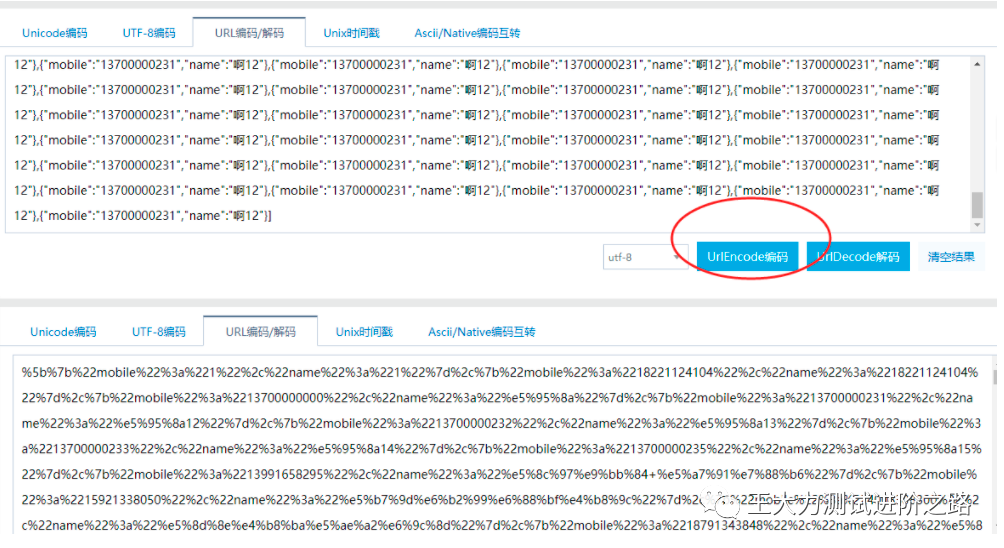
        设置请求拦截，再次操作通讯录导入，请求被拦截未发送至服务端，快速修改textview中参数为编码好的5000+手机号，点绿色run to completion运行释放请求拦截，请求发送至服务端，服务端响应至客户端，客户端展示处理效果，5000+个手机号正常展示，达到了测试的效果。