哈夫曼树是一种带权路径长度最短的二叉树,也称为最优二叉树。下面用一幅图来说明。
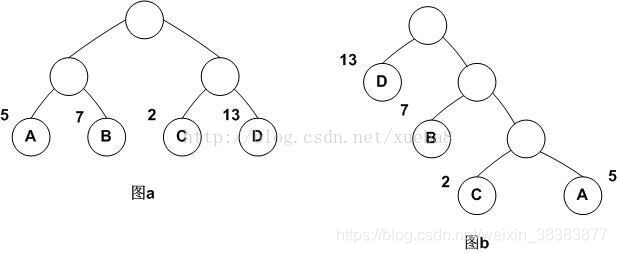
它们的带权路径长度分别为:
图a: WPL=5*2+7*2+2*2+13*2=54
图b: WPL=5*3+2*3+7*2+13*1=48
可见,图b的带权路径长度较小,我们可以证明图b就是哈夫曼树(也称为最优二叉树)。
哈夫曼树构建教程
例:对于给定的一组权值w={1,4,9,16,25,36,49,64,81,100},构造具有最小带权外部路径长度的扩充二叉树,并求出他的的带权外部路径长度。
解:1、首先我们对这一组数字进行排序。规则是从小到大排列(题目已排序好)。
2、在这些数中 选择两个最小的数字(哈夫曼树是从下往上排列的)写在纸上。如下图所示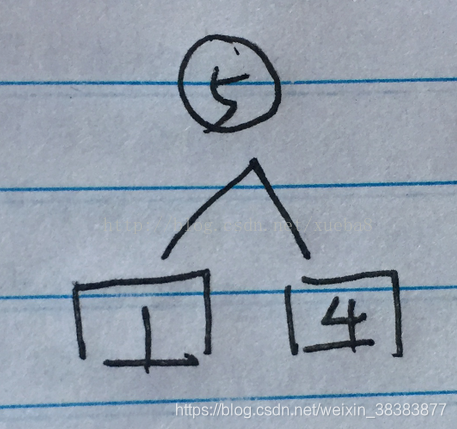
3、用一个类似于树杈的“树枝”连接上两个最小的数。在顶点处计算出这两个数字的和 并写在上面。然后再比较剩下的数字和这个和的大小,再取出两个最小的数字进行排列
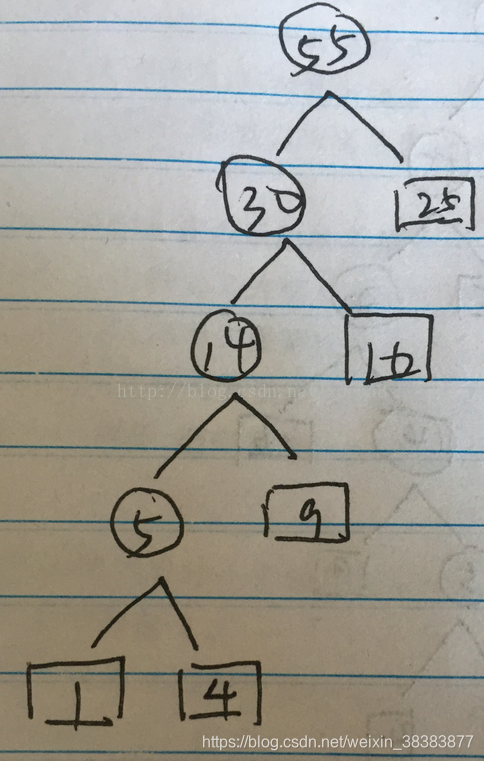
4、如上图中30,25的和为55,已经大于36,49.所以这个时候开始有分支,用36,49再构造一个分支,如下图。
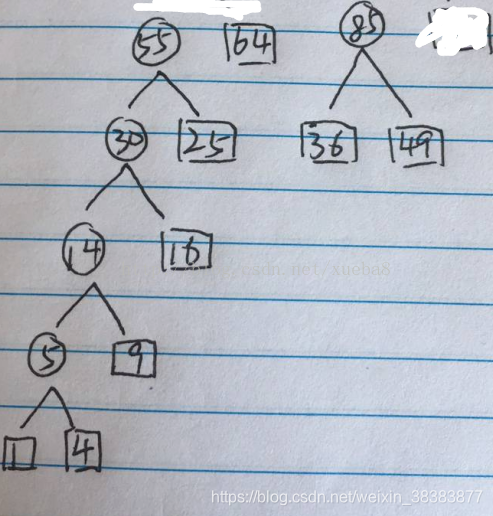
5、最后将分支合并成一个二叉树,如下图
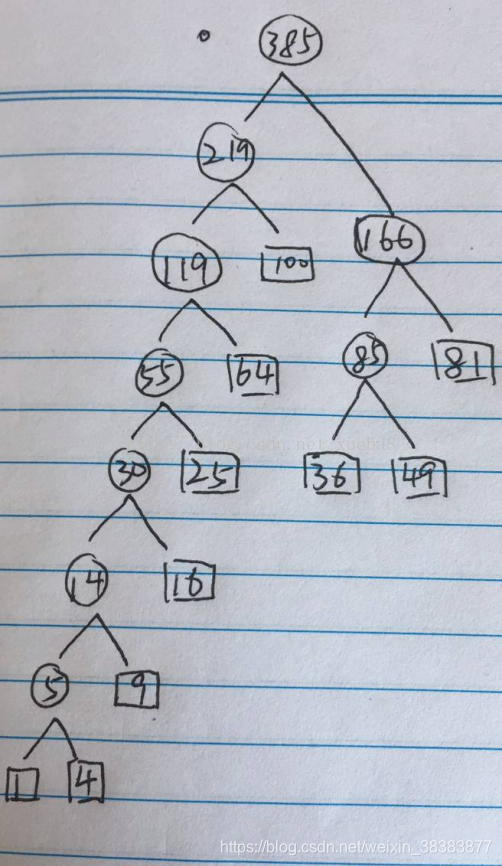
6、这样,二叉树结构就构建好了。
带权外部路径长度计算;
WPL=2*100 + 3*64 + 2*81 + 4*25 + 2*49 + 2*36 + 5*16 + 6*9 + 7*1 + 7*4 =993
(385的权重为0,216和166权重为1.....)
左0右1:哈夫曼编码为: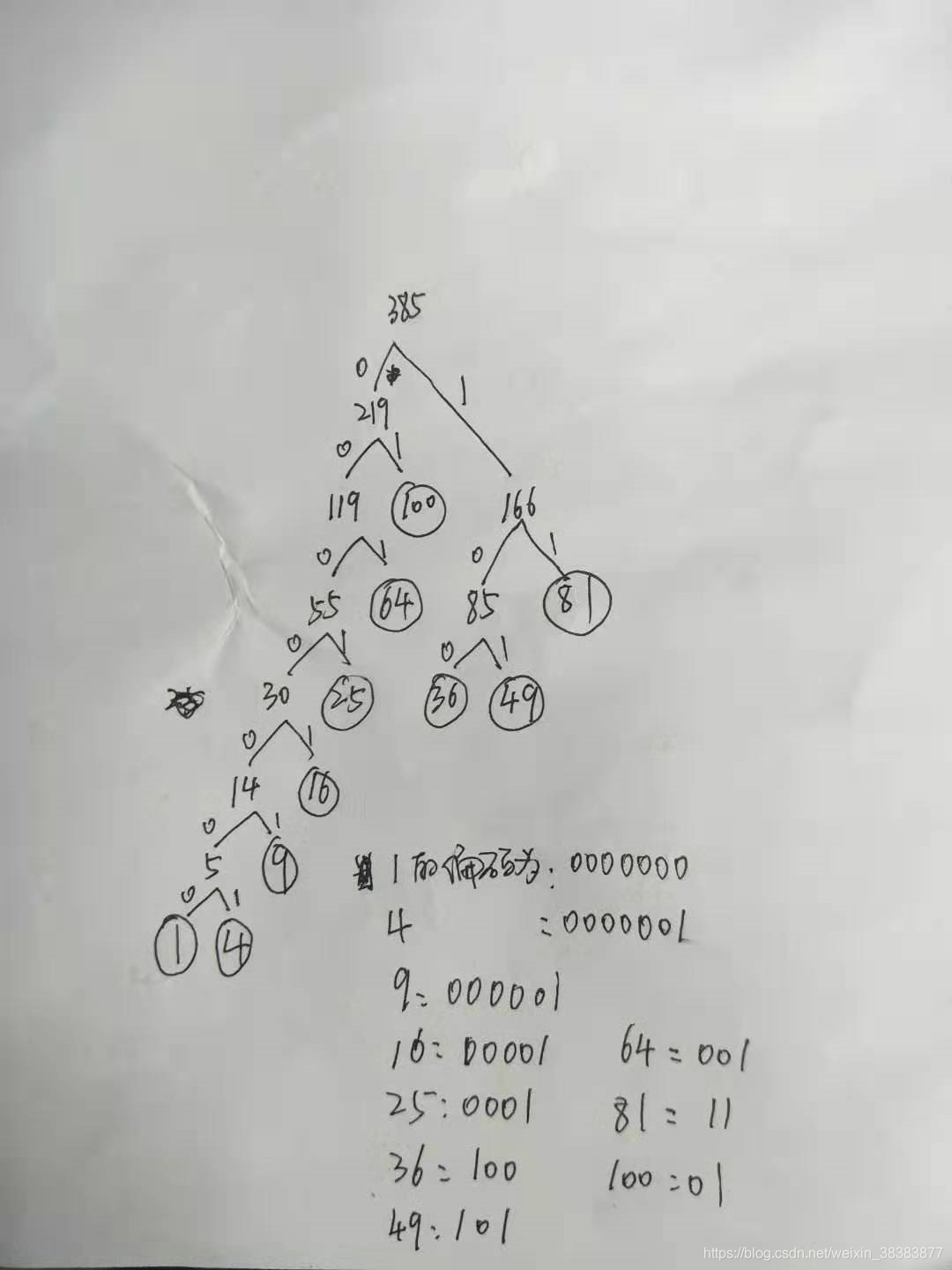
















![ios 获取html中的json数据,[IOS]UIWebView实现保存页面和读取服务器端json数据](http://pic.xiahunao.cn/ios 获取html中的json数据,[IOS]UIWebView实现保存页面和读取服务器端json数据)
的方法)

