
对于整个中考数学来说,二次函数的重要性,我想不用老师多说,大家肯定心里有数。二次函数作为初中数学的重要内容,命题老师很喜欢把它与其他几何图形进行结合,形成综合性更强的试题。
不可否认,二次函数与几何有关的试题已经成为近年来中考数学的热点试题之一,此类试题不仅可以考查二次函数和平面几何的基础知识,还可以考查数形结合、分类讨论等数学思想方法,以及考生的阅读理解探究能力、收集处理信息的能力、运用数学知识解决问题的能力等。
二次函数在中学数学中占有重要地位,因此它一直是压轴题的热门对象,综观近几年全国各地的中考数学压轴题,你会发现大多是二次函数与圆、三角形、四边形等知识结合的综合问题,具有一定的综合性和较大的难度。
在中考数学中,二次函数与几何有关的综合试题已经成为很多考生头痛的问题,这既是难点问题,又是考查考生分析问题和解决问题的能力,在中考数学中占有重要的地位。
如何解决此类问题?除了要加强训练以外,还要注重思维方法的训练以及良好的解题习惯。

二次函数与几何有关的中考试题分析,讲解1:
如图所示,过点F(0,1)的直线y=kx+b与抛物线y=x2/4交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2>0).
(1)求b的值.
(2)求x1•x2的值.
(3)分别过M,N作直线l:y=-1的垂线,垂足分别是 M1和N1.判断△M1FN1的形状,并证明你的结论.
(4)对于过点F的任意直线MN,是否存在一条定直线 m,使m与以MN为直径的圆相切.如果有,请求出这条直线m的解析式;如果没有,请说明理由.


考点分析:
二次函数综合题;代数几何综合题。
题干分析:
(1)把点F的坐标代入直线可以确定b的值.
(2)联立直线与抛物线,代入(1)中求出的b值,利用根与系数的关系可以求出x1•x2的值.
(3)确定M1,N1的坐标,利用两点间的距离公式,分别求出M1F2,N1F2,M1N12,然后用勾股定理判断三角形的形状.
(4)根据题意可知y=-1总与该圆相切.
解题反思:
本题考查的是二次函数的综合题,(1)由点F的坐标求出b的值.(2)结合直线与抛物线的解析式,利用根与系数的关系求出代数式的值.(3)用两点间的距离公式,判断三角形的形状.(4)根据点与圆的位置判断直线与圆的位置.

二次函数与几何有关的中考试题分析,讲解2:
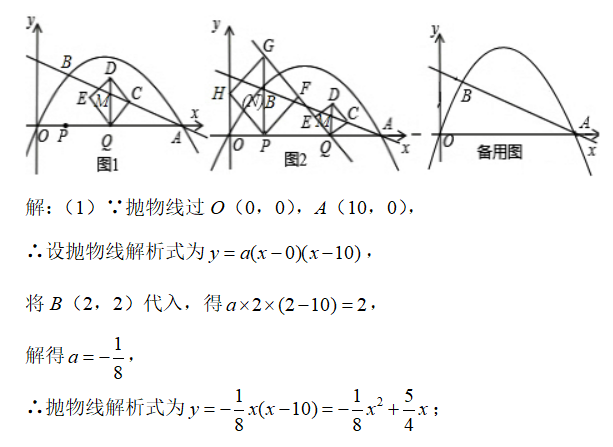
如图1,在平面直角坐标系中,抛物线过原点O,点A(10,0)和点B(2,2),在线段OA上,点P从点O向点A运动,同时点Q从点A向点O运动,运动过程中保持AQ=2OP,当P、Q重合时同时停止运动,过点Q作X轴的垂线,交直线AB于点M,延长QM到点D,使MD=MQ,以QD为对角线作正方形QCDE(正方形QCDE岁点Q运动).
(1)求这条抛物线的函数表达式;
(2)设正方形QCDE的面积为S,P点坐标(M,0)求S与M之间的函数关系式;
(3)过点P作X轴的垂线,交抛物线于点N,延长PN到点G,使NG=PN,以PG为对角线作正方形PFGH(正方形PFGH随点P运动),当点P运动到点(2,0)时,如图2,正方形PFGH的边GP和正方形QCDE的边EQ落在同一条直线上.
①则此时两个正方形中在直线AB下方的阴影部分面积的和是多少?
②若点P继续向点A运动,还存在两个正方形分别有边落在同一条直线上的情况,请直接写出每种情况下点P的坐标,不必说明理由.


考点分析:
二次函数综合题;综合题。
题干分析:
(1)抛物线与X轴交于O、A两点,设抛物线的交点式,将B点坐标代入,可求抛物线解析式;
(2)根据A(10,0),B(2,2)求直线AB的解析式,由AQ=2OP=2M,得到OQ=OA﹣AQ=10﹣2M,代入直线AB的解析式,可求M点纵坐标,得出QD的表达式,根据S=QD2/2求解;
(3)①将X=2代入抛物线解析式得Y=2,可知N(2,2),G(2,4),当GF和EQ落在同一条直线上时,△FGQ为等腰直角三角形,则PQ=PG=4,OQ=OP+PQ=6,代入直线AB解析式得M(6,1),即QM=1,由旋转法可知,每一个阴影部分面积等所在正方形面积的一半,由此可求两个阴影部分面积和;
②分为PF、DE,PF、CQ,PH、CD,三种情况,求出相应的P点坐标.
解题反思:
本题考查了二次函数的综合运用.关键是根据正方形对角线的性质及其与X轴垂直解题。
面对二次函数与几何有关的问题,不少考生对此望而生畏,缺乏思路,感到无从下手,难以拿到分数。事实上,只要我们理清思路,方法适当,稳步推进,少失分,多得分,得高分是完全可以做到的。
——————————END——————————
▽
初中学习资料下载,
中考复习资料下载(各学科)
△
欢迎大家登陆学习平台。
学习平台官方网站第一中考
网址是www.diyizhongkao.com

中考数学宝典→客服微信号是czzksxbd
点击原文,获取更多学习资料??












.ppt)





