目录

​编辑

一，问题描述

二，例子

 三，题目接口

四，题目解答

1，暴力解法

2.规律解法

总结：

代码：

 

---

 

 

一，问题描述

输入一个整数 n ，求1～n这n个整数的十进制表示中1出现的次数。

例如，输入12，1～12这些整数中包含1 的数字有1、10、11和12，1一共出现了5次。

二，例子

先来看看题目的例子：

在例1中给出的n=12，那答案便是5。为什么呢？先来看看1~12之间的数字：

1，2，3，4，5，6，7，8，9，10，11，12。在这一组数字中，出现1的数字有：1，10，11，12。刚好就是5五个所以答案就是5。

 三，题目接口

class Solution {
public:int countDigitOne(int n) {}
};

四，题目解答

1，暴力解法

不得不说，暴力解法写起来特别简单。一个for循环加上一个while循环便可以了。其中for循环的作用便是用来将1~n的数字遍历，while循环的作用是求遍历进来的数的每一位上的数字是否为1。根据以上思路写出的代码如下：

class Solution {
public:int countDigitOne(int n) {int count = 0;for(int i  = 1;i<=n;i++){int j = i;while(j){if(j%10==1){count++;}j/=10;}}return count;}
};

但是，遗憾的告诉大家这个代码是过不了的。因为n可以变得很大：

 在这里将count改为long long 类型也没有用。

2.规律解法

在这里先说一下这个解法的步骤：

1.首先来定义几个变量：cur,high,cur,bit,ans。这几个变量都是一些数字。对于一个数520122，它们的对应关系如下：

 对于现在这个cur指向最低位的2时，我们可以假设cur指向的数字变成了1。对于这个最后一位为1时这个六位数有多少个组合呢？是不是有（52012+1） = （high+1)种组合啊？如下图：

现在cur往前移一位，变成下面的样子：

 

 

还是将cur指向的2变成1，这个时候对于十位上的数变成1会有多少种组合呢？

对于右边还是(5201+1)=(high+1)种。但是对于左边可不是（2+1） = （low+1)种。而是bit种。为什么呢？因为当cur指向的数字大于1时，那cur的下一位便可以变成0~9中的任何一个数字共有10种。也就是bit种。所以这里的组合有（5201+1)*10 =(high+1)*bit种。

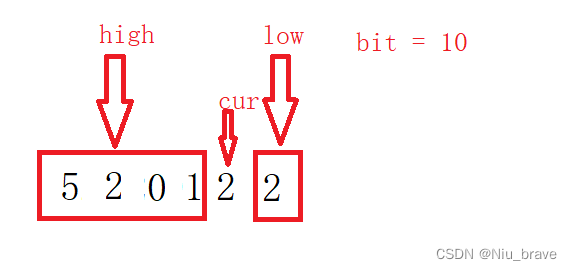
       接下来再次移动cur，如下图：

 这时对于cur指向的数字为1时的搭配便是520*100+(22+1) = high*bit+（low+1)种了。

因为cur指向的是数字1，所以为了保证搭配成的组合数比n小。high指向的组合可以分为两种情况。1,high取到了520，那此时low只能取：00~22。2.当high取到：000~519这520种情况时，那low可以取：00~99共100种，也就是bit种。

    现在继续移动cur：

此时cur指向的数字变成了0。若要让该位置上的数字变成1并且让得到的数字比n小，那high就只能取到：00~51共52个数，在取这52个数是low是没有限制的，所以low可以取到0~999的数字。所以当cur位为1时共有52*1000 =high*bit种搭配。 

总结：

求到这时规律已经出现：

cur>1共有：（high+1)*bit种

cur = 1共有：hight*bit+(low+1)种

cur = 0共有：hight*bit种

并且：

cur = （n/bit)%10

low = n%bit

hight = n/bit/10。

代码：

class Solution {
public:int countDigitOne(int n) {long long sum = 0;long long bit = 1;while(bit<=n){long long cur = (n/bit)%10;long long low = n%bit;long long high = n/bit/10;if(cur == 0){sum+=high*bit;}else if(cur == 1){sum+=high*bit+(low+1);}else{sum+=(high+1)*bit;}bit*=10;}return sum;}
};