目录
一、基本概念
二、概念的数学形式表达
三、确定w和b
1.读取或输入数据
2.归一化、标准化
2.1 均值
2.2 归一化
2.3 标准化
3.求解w和b
1.直接解方程
2.最小二乘法(least square method)求解:
4. 评估回归模型
四、sklearn中的线性回归
1.对数据进行解析
2.对原始值和预测值进行绘图
3.绘制残差图
一、基本概念
线性(linear):
指量与量之间按比例、成直线的关系,在空间和时间上代表规则和光滑的运动,一阶导数为常数
非线性(non-linear):
指不按比例、不成直线的关系,代表不规则的运动和突变,一阶导数不为常数。
一个线性的例子:
数据:工资和年龄(2个特征)
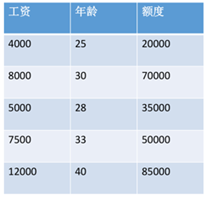
目标:预测银行会贷款给我多少钱(标签)
考虑:工资和年龄都会影响最终银行贷款的结果,那么他们各自有多大的影响呢?(参数)
通俗的解释:
x1,x2就是我们的两个特征(年龄、工资),y是银行最终会借给我们多少钱
找到最合适的一条线(想象一个高维)来最好的拟合我们的数据点

数学形式来了

二、概念的数学形式表达
给定数据集:
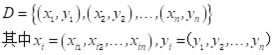
数据的矩阵形式:
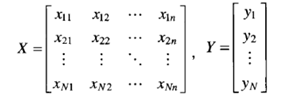
线性模型(linear model)试图学得一个通过属性组合的线性组合来进行预测的函数,即
![]()
用向量形式写成:

线性回归(linear regression)试图学得一个线性模型以尽可能准确地预测实值输出标记
![]()
三、确定w和b
对离散属性:
若属性间存在“序”关系,可通过连续化将其转化为连续值。
若属性间不存在“序”关系,则转化为k维向量。

1.读取或输入数据

#导入相关库 numpy pandas
import pandas
import numpy
#如果没有请安装哦,如下
# pip install pandas
# pip install numpy有库了,我们才可以导入数据哇
首先我们先看看csv数据的导入
import pandas as pd文件
data = pd.read_csv(r'路径', encoding='gbk')
#读取csv数据方式 pd.read_csv
# encoding='gbk' 定义编码方式 常用只有两种 utf8 和 gbk 按需定义即可#下面这种读取是显示没有第一列的数据 index_col=0 python中第0列也就是实际的第1列
#reset_index(drop=True) True表示执行此删除命令
data= pd.read_csv(r"路径", encoding='gbk', index_col=0).reset_index(drop=True)
读取数据后得分出和为X,何为Y
X = data.iloc[:,0:4] # 0到3列所有的数据也就是实际的1到4列
Y = data.iloc[:, 5] # 第5列所有的数据也就是实际的第6列接下来我们看看自己建立矩阵的数据读取方式
import numpy as np
a = np.array([1,2,3])
print(a)
b = np.array([[1,2],[2,3]])
print(b)返回:
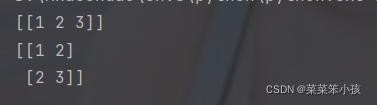
说到矩阵了,就顺便说一下
创建矩阵的相关知识:mat() 创建矩阵array() 将列表转换为数组,可选择显式指定dtypearange() range的numpy版,支持浮点数linspace() 类似arange(),第三个参数为数组长度zeros() 根据指定形状和dtype创建全0数组ones() 根据指定形状和dtype创建全1数组empty() 根据指定形状和dtype创建空数组(随机值)eye() 根据指定边长和dtype创建单位矩阵
2.归一化、标准化
2.1 均值
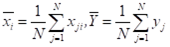
# 在这里我们可以直接用numpy中的mean函数计算
numpy。mean()顺便介绍一下其他的numpy中的相关常用函数:
sum 求和
cumsum 求前缀和
mean 求平均数
std 求标准差
var 求方差
min 求最小值
max 求最大值
argmin 求最小值索引
argmax 求最大值索引
要想确定w和b,首先要视情况决定是否需要对数据进行归一化或标准化

2.2 归一化
#范围归一化 此方法只适用一维数据
import numpy as np
data = np.asarray([1,5,3,8,4])
for x in data:x = float(x - np.min(data))/(np.max(data)- np.min(data))print(x)# sklearn中的范围归一化函数MinMaxScaler函数可适用多维数据
from sklearn import preprocessing
import numpy as np X = np.array([[ 1., -1., 2.], [ 2., 0., 0.], [ 0., 1., -1.]]) min_max_scaler = preprocessing.MinMaxScaler()
x = min_max_scaler.fit_transform(X)2.3 标准化
#标准化
import numpy as npcc = np.array([[1,2,3],[4,5,6]]) #创建矩阵
print(cc) #输出矩阵cc_mean = np.mean(cc, axis=0) #axis=0,表示按列求均值 ——— 即第一维,每一列可看做一个维度或者特征
cc_std = np.std(cc, axis=0) #xis=0,表示按列求标准差
cc_zscore = (cc-cc_mean)/cc_std #直接计算,对数组进行标准化,一定要注意维度
print(cc_zscore) #输出结果#sklearn中的标准化
from sklearn.preprocessing import StandardScalerscaler = StandardScaler()
cc_zscore = scaler.fit_transform(cc)
print(cc_zscore) #输出结果
3.求解w和b
1.直接解方程

N = data.shape[0]
X_mean = np.mean(X) #求均值
X_mean = np.array(X_mean) #转为数组
Y_mean = np.mean(Y) #求均值
Y_mean = np.array(Y_mean) #转为数组A = np.dot(X.T,X)-N*np.dot(X_mean.T,X_mean)
C = np.dot(X.T,Y)-N*np.dot(X_mean.T,Y_mean)
B = np.dot(np.linalg.inv(A),C) #系数
BB = Y_mean - np.dot(X_mean,B.T) #常数
YY = np.dot(X,B.T)+BB #Y的估计值2.最小二乘法(least square method)求解:
把数据集D表示为一个m*(d+1)大小的矩阵X,其中每行对应于一个示例,改行前d个元素对应于示例的d个属性值,最好一个元素恒置为1,即

x = np.array([[1,5,8],[2,5,8],[1,4,6]])
Y = np.array([2,5,3])
b = np.ones(3)
X = np.insert(x, 3, values=b, axis=1)当X^TX 为满秩矩阵(full-rank matrix) 或正走矩阵(positive definite matrix) 时,令
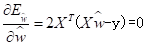
得到
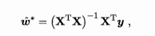
w=np.dot(np.dot(np.linalg.inv(np.dot(X.T,X)),X.T),Y)其中(X^TX)^-l是矩阵(X^TX)的逆矩阵.令xi = (xi ,l) ,则最终学得的多元线性回归模型为
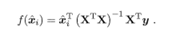
4. 评估回归模型

#离差平方和
S = np.var(Y)
#回归平方和
U = np.var(YY)
#剩余平方和
Q = S - U
#复可决系数
R2 = U/S
#负相关系数
R = np.sqrt(U/S)
#回归均方
# n= X_mean 的个数
UU = U/n
#剩余均方
# N= Y的个数
QQ = Q/(N-n-1)
#剩余标准差
s = np.sqrt(QQ)
#方程显著性检验值
F = UU/QQ四、sklearn中的线性回归
1.对数据进行解析
from sklearn import linear_model
import numpy as np
import pandas as pd
#使用最小二乘线性回归进行拟合,导入相应的模块
lr=linear_model.LinearRegression()
data = pd.read_csv(r'D:\桌面\A.csv', encoding='gbk')
X = data.iloc[:,0:4]
Y = data.iloc[:, 5]
X_train,X_test,Y_train,Y_test=train_test_split(X, Y, test_size=0.2, random_state=0)
lr.fit(X_train,Y_train) #拟合
y=lr.predict(X) #得到预测值集合y
coef=lr.coef_ #获得该回该方程的回归系数与截距
intercept=lr.intercept_
print("预测方程回归系数:",coef)
print("预测方程截距:",intercept)
score=lr.score(X_test,Y_test) #对得到的模型打分
print('模型的预测分',score)2.对原始值和预测值进行绘图
from matplotlib import pyplot as plt
plt.plot(range(1,len(Y)+1),Y)
plt.plot(range(1,len(Y)+1),y)
plt.show()3.绘制残差图
err = y - Y #求残差
plt.plot(range(1,len(Y)+1),err)
plt.show()
)

之读写文件)















