目录
1.简介
2.Pearson相关系数
算法详解
程序实现
3.Kendall相关系数
算法详解
程序实现
4.Spearman相关系数
算法详解
程序实现
1.简介
相关性分析是指对两个或多个具备相关性的变量元素进行分析，从而衡量两个变量因素的相关密切程度。相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。
常见的三种：Pearson相关系数，Kendall相关系数和Spearman相关系数。在这三大相关系数中，spearman和kendall属于等级相关系数亦称为“秩相关系数”，是反映等级相关程度的统计分析指标。最终选择哪种相关系数法，对比结果谁更符合预期效果。
2.Pearson相关系数
算法详解
按照大学的线性数学水平来理解, 它比较复杂一点,可以看做是两组数据的向量夹角的余弦。
常见Pearson有以下几种公式，以下三种公式皆等价
皮尔森相关系数是衡量线性关联性的程度，公式定义为：两个连续变量(X,Y)的pearson相关性系数P(x,y)等于它们之间的协方差cov(X,Y)除以它们各自标准差的乘积(σX,σY)。系数的取值总是在-1到1之间，接近0的变量被成为无相关性，接近1或者-1被称为具有正向或者负向强相关性。
那么皮尔森适用的条件是什么呢？
-
两个变量之间是线性关系，都是连续数据。
-
两个变量的总体是正态分布，或接近正态的单峰分布。
-
两个变量的观测值是成对的，每对观测值之间相互独立。
在满足这些条件后，接下来我们来看下程序，这三种相关系数均可用corr函数实现
①当X与Y是构成一个矩阵时，关于两者相关系数程序格式为
corr(X,Y,'type','Pearson')
②当X是由多个指标数据构成的矩阵时，关于指标间相关系数程序格式为
corr(X,'type','Pearson')
程序实现
数据如下：
代码如下：
#导入相关库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
#导入数据
data=pd.read_excel(r'D:\桌面\xiangguan.xlsx')
# print(data)
#皮尔森相关系数
pearson=data.corr(method="pearson")
# print(pearson)
# data.corr(method="pearson")
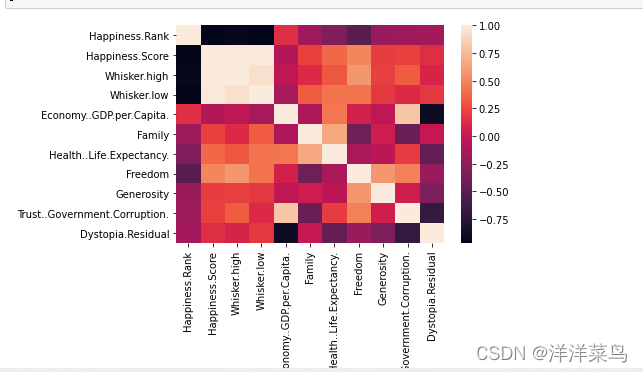
#绘制热力图
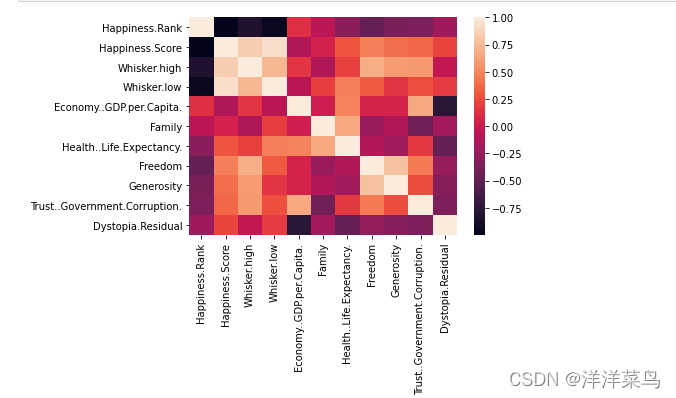
sns.heatmap(pearson)
plt.show()返回：
3.Kendall相关系数
Kendall相关系数：是一个用来测量两个随机变量相关性的统计值，在一个肯德尔检验是一个无参数假设检验，它使用计算而得的相关系数去检验两个随机变量的统计依赖性。肯德尔相关系数的取值范围在-1到1之间，当τ为1时，表示两个随机变量拥有一致的等级相关性；当τ为-1时，表示两个随机变量拥有完全相反的等级相关性；当τ为0时，表示两个随机变量是相互独立的。
算法详解
这里有三种公式计算肯德尔相关系数：
其中C表示XY中拥有一致性的元素对数（两个元素为一对）；D表示XY中拥有不一致性的元素对数，N为元素个数。
注意：这一公式仅适用于集合X与Y中均不存在相同元素的情况（集合中各个元素唯一）
注意：这一公式适用于集合X或Y中存在相同元素的情况（当然，如果X或Y中均不存在相同的元素时，公式2便等同于公式1）
其中，C表示XY中拥有一致性的元素对数（两个元素为一对）；D表示XY中拥有不一致性的元素对数。
N1、N2分别是针对集合X、Y计算的，将X中的相同元素分别组合成小集合，Y同理，s、t表示集合X、Y中拥有的小集合数（例如X包含元素：12 3 4 3 3 2，那么这里得到的s则为2，因为只有2、3有相同元素），Ui表示第i个小集合所包含的元素数，Vi同理。
①当X与Y是构成一个矩阵时，关于两者相关系数程序格式为
corr(X,Y,'type','Kendall')
②当X是由多个指标数据构成的矩阵时，关于指标间相关系数程序格式为
corr(X,'type','Kendall')
程序实现
数据如下：
代码如下：
#导入相关库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
#导入数据
data=pd.read_excel(r'D:\桌面\xiangguan.xlsx')
#kendall相关系数
kendall=data.corr(method="kendall")
# print(kendall)
# data.corr(method="kendall")
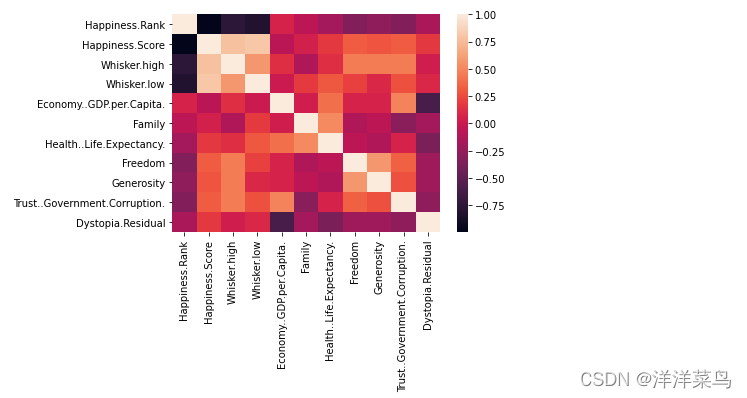
#绘制热力图
sns.heatmap(kendall)
plt.show()返回：
4.Spearman相关系数
Spearman相关系数：Spearman等级相关系数又称秩相关系数。利用两变量的秩次大小作线性相关分析，Spearman等级相关系数用来估计两个变量X、Y之间的相关性，其中变量间的相关性可以使用单调函数来描述。如果两个变量取值的两个集合中均不存在相同的两个元素，那么，当其中一个变量可以表示为另一个变量的很好的单调函数时（即两个变量的变化趋势相同），两个变量之间的ρ可以达到+1（绝对正相关）或-1（绝对负相关）
算法详解
Spearman相关系数可由以下两式计算
1、将集合x、y中的元素对应相减得到一个排行差分集合d，由排行差分集合d计算而得
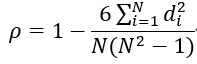
2、由排行集合x、y计算而得（斯皮尔曼等级相关系数同时也被认为是经过排行的两个随即变量的皮尔逊相关系数，以下实际是计算x、y的皮尔逊相关系数）
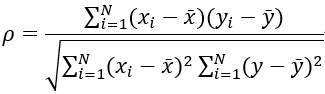
以下是一个计算集合中元素排行的例子（仅适用于斯皮尔曼等级相关系数的计算）
这里需要注意：当变量的两个值相同时，它们的排行是通过对它们位置进行平均而得到的
适用范围：只需两个变量的观测值是成对的等级评定数据，或者是由连续变量观测数据转化得到的等级数据，不论两个变量的总体分布形态、样本容量的大小如何，都可以用斯皮尔曼等级相关系数来进行研究
程序实现
数据如下：
代码如下：
#导入相关库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
#导入数据
data=pd.read_excel(r'D:\桌面\xiangguan.xlsx')
#Spearman相关系数
spearman=data.corr(method="spearman")
# print(spearman)
# data.corr(method="spearman")
#绘制热力图
sns.heatmap(spearman)
plt.show()返回：
