博弈论 —— python

1.简介

2.算法原理

3.实例分析

1.各参数初始化

2.计算期望与实际期望

3.博弈过程

4.绘图

完整代码

1.简介

博弈论又被称为对策论(Game Theory)既是现代数学的一个新分支，也是运筹学的一个重要学科。

博弈论主要研究公式化了的激励结构间的相互作用。是研究具有斗争或竞争性质现象的数学理论和方法。博弈论考虑游戏中的个体的预测行为和实际行为，并研究它们的优化策略。生物学家使用博弈理论来理解和预测进化论的某些结果。

博弈论已经成为经济学的标准分析工具之一。在生物学、经济学、国际关系、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。

基本概念中包括局中人、行动、信息、策略、收益、均衡和结果等。其中局中人、策略和收益是最基本要素。局中人、行动和结果被统称为博弈规则。

博弈论简单讲就是，A采取措施影响B的行为，B的行为影响A的决策，两者来回博弈，最终达到一个动态平衡。博弈论严格来讲只是一种解题方式。

2.算法原理

以电动出租车与换电站为例，假设电动出租车及换电站均属于同一家公司，公司想通过换电站价格定价措施去控制目标区域内的出租车数量达到预期分布。

对于司机而言，有两个成本，一个是距离成本d，一个是支付成本p，支付成本即是换电池所支付的电价，我们可以设立权重因子a将两者合并构建为一个效用函数，司机会选择该函数最小的换电站更换电池，更换电池后司机一般会在周围开始接单

对于公司而言，目标函数则是不同地区的出租车实际分布e与期望分布E的绝对差之和，公司通过调整价格去影响司机的选择，从而调整司机在不同区域的分布

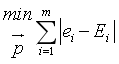
双层博弈论的模型分析

①第一阶段，充电站统计出各电动出租车的换电请求后，根据优化目标，制定价格策略

②第二阶段，电动出租车根据自身效用函数从所有换电站中选择出目标换电站进行跟换电池

③第一阶段和第二阶段交替往复进行，直到达到均衡

算法设计步骤

3.实例分析

1.各参数初始化

n=900 #换电需求数
min_price=170 #换电价格范围
max_price=230
A=np.random.normal(36, 5, 25) #初始期望，平均值为36，方差为5的高斯分布
E=np.floor(A)#朝0方向取整，如，4.1，4.5，4.8取整都是4
# 下面是根据需求数调整E的大小
E=np.floor(A)
a=sum(E)-n
A=A-a/25
E=np.floor(A)
b=sum(E)-n
A=A-b/25
E=np.floor(A)
a1=0.05;a2=0.95;#距离成本与换点价格权重
x=[random.random()*20000 for i in range(n)]#初始化需求车辆位置
y=[random.random()*20000 for i in range(n)]
H=np.mat([[2,2],[2,6],[2,10],[2,14],[2,18],[6,2],[6,6],[6,10],[6,14],[6,18],[10,2],[10,6],[10,10],[10,14],[10,18],[14,2],[14,6],[14,10],[14,14],[14,18],[18,2],[18,6],[18,10],[18,14],[18,18]])*1000
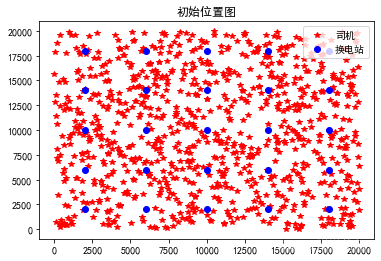
# 制初始化的司机与换电站的位置图
plt.plot(x,y,'r*')
plt.plot(H[:,0],H[:,1],'bo')
plt.legend(['司机','换电站'], loc='upper right', scatterpoints=1)
plt.title('初始位置图')
plt.show()

# 计算期望与实际期望
D=np.zeros((len(H),n)) #需求车辆到各换电站的需求比例
price=200*np.ones((1,25))
for i in range(len(H)):for j in range(len(x)):D[i,j]=a1*np.sqrt(((H[i,0]-x[j]))**2+(H[i,1]-y[j])**2)+a2*price[0,i]D=D.T #转置
D=D.tolist() #转为列表格式
d2=[D[i].index(np.min(D[i])) for i in range(n)]
C = Counter(d2)
e=list(C.values())
err=sum(abs(E-e)) #期望差之和，即博弈对象
print(err)

返回：因为随机，所有每次结过可能不一样

3.博弈过程

J=[] #价格变化的差值
ER=[err] #E-e的变化差值
for k in range(1,100):j=0for i in range(25):if e[i] < E[i] and price[0,i] >= min_price:price[0,i] = price[0,i]-1j=j+1if e[i] > E[i] and price[0,i] <= max_price:price[0,i] = price[0,i]+1j=j+1J.append(j)DD=np.zeros((len(H),n)) #需求车辆到各换电站的需求比例
#     price=200*np.ones((1,25))for i in range(len(H)):for j in range(len(x)):DD[i,j]=a1*np.sqrt(((H[i,0]-x[j]))**2+(H[i,1]-y[j])**2)+a2*price[0,i]DD=DD.T #转置DD=DD.tolist() #转为列表格式dd2=[DD[i].index(np.min(DD[i])) for i in range(n)]C = Counter(dd2)e=[C[i] for i in sorted(C.keys())]err=sum(abs(E-e)) #期望差之和，即博弈对象ER.append(err)

4.绘图

#绘制图
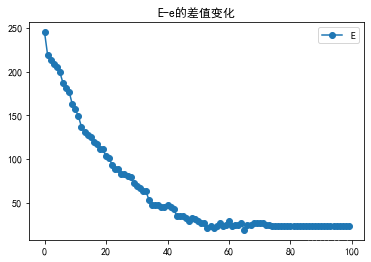
plt.plot(ER,'-o')
plt.title('E-e的差值变化')
# plt.set(gcf,'unit','normalized','position',[0.2,0.2,0.64,0.32])
plt.legend('E-e')
# plt.grid(ls=":",c='b',)#打开坐标网格
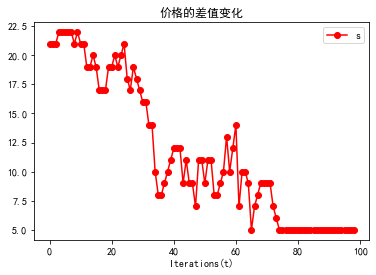
plt.show()plt.plot(J,'r-o')
plt.title('价格的差值变化')
plt.xlabel('Iterations(t)')
plt.legend('sum of Price(t)-Price(t-1)')
# plt.grid(ls=":",c='b',)#打开坐标网格
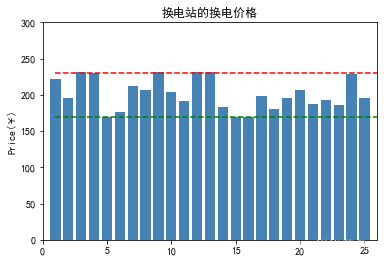
plt.show()plt.bar(x = range(1,26), # 指定条形图x轴的刻度值height=price[0],color = 'steelblue',width = 0.8)
plt.plot([1,26],[min_price,min_price],'g--')
plt.plot([1,26],[max_price,max_price],'r--')
plt.title('换电站的换电价格')
plt.ylabel('Price(￥)')
plt.axis([0,26,0,300])
# plt.grid(ls=":",c='b',)#打开坐标网格
plt.showindex = np.arange(1,26)
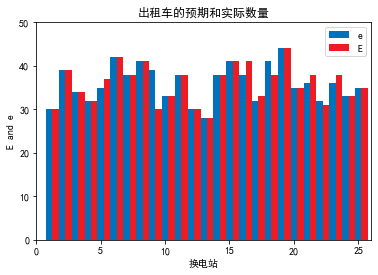
rects1 = plt.bar(index, e, 0.5, color='#0072BC')
rects2 = plt.bar(index + 0.5, E, 0.5, color='#ED1C24')
plt.axis([0,26,0,50])
plt.title('出租车的预期和实际数量')
plt.ylabel('E and e')
# plt.grid(ls=":",c='b',)#打开坐标网格
plt.xlabel('换电站')
plt.legend(['e','E'])
plt.show()

#导入相关库
import numpy as np
import math
import random
from collections import Counter
import matplotlib.pyplot as plt
#解决图标题中文乱码问题
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题#初始化各参数
n=900 #换电需求数
min_price=170 #换电价格范围
max_price=230
A=np.random.normal(36, 5, 25) #初始期望，平均值为36，方差为5的高斯分布
E=np.floor(A)#朝0方向取整，如，4.1，4.5，4.8取整都是4
# 下面是根据需求数调整E的大小
E=np.floor(A)
a=sum(E)-n
A=A-a/25
E=np.floor(A)
b=sum(E)-n
A=A-b/25
E=np.floor(A)
a1=0.05;a2=0.95;#距离成本与换点价格权重
x=[random.random()*20000 for i in range(n)]#初始化需求车辆位置
y=[random.random()*20000 for i in range(n)]
H=np.mat([[2,2],[2,6],[2,10],[2,14],[2,18],[6,2],[6,6],[6,10],[6,14],[6,18],[10,2],[10,6],[10,10],[10,14],[10,18],[14,2],[14,6],[14,10],[14,14],[14,18],[18,2],[18,6],[18,10],[18,14],[18,18]])*1000
# 制初始化的司机与换电站的位置图
plt.plot(x,y,'r*')
plt.plot(H[:,0],H[:,1],'bo')
plt.legend(['司机','换电站'], loc='upper right', scatterpoints=1)
plt.title('初始位置图')
plt.show()# 计算期望与实际期望
D=np.zeros((len(H),n)) #需求车辆到各换电站的需求比例
price=200*np.ones((1,25))
for i in range(len(H)):for j in range(len(x)):D[i,j]=a1*np.sqrt(((H[i,0]-x[j]))**2+(H[i,1]-y[j])**2)+a2*price[0,i]D=D.T #转置
D=D.tolist() #转为列表格式
d2=[D[i].index(np.min(D[i])) for i in range(n)]
C = Counter(d2)
e=list(C.values())
err=sum(abs(E-e)) #期望差之和，即博弈对象#博弈过程
J=[] #价格变化的差值
ER=[err] #E-e的变化差值
for k in range(1,100):j=0for i in range(25):if e[i] < E[i] and price[0,i] >= min_price:price[0,i] = price[0,i]-1j=j+1if e[i] > E[i] and price[0,i] <= max_price:price[0,i] = price[0,i]+1j=j+1J.append(j)DD=np.zeros((len(H),n)) #需求车辆到各换电站的需求比例
#     price=200*np.ones((1,25))for i in range(len(H)):for j in range(len(x)):DD[i,j]=a1*np.sqrt(((H[i,0]-x[j]))**2+(H[i,1]-y[j])**2)+a2*price[0,i]DD=DD.T #转置DD=DD.tolist() #转为列表格式dd2=[DD[i].index(np.min(DD[i])) for i in range(n)]C = Counter(dd2)e=[C[i] for i in sorted(C.keys())]err=sum(abs(E-e)) #期望差之和，即博弈对象ER.append(err)#绘制图
plt.plot(ER,'-o')
plt.title('E-e的差值变化')
# plt.set(gcf,'unit','normalized','position',[0.2,0.2,0.64,0.32])
plt.legend('E-e')
# plt.grid(ls=":",c='b',)#打开坐标网格
plt.show()plt.plot(J,'r-o')
plt.title('价格的差值变化')
plt.xlabel('Iterations(t)')
plt.legend('sum of Price(t)-Price(t-1)')
# plt.grid(ls=":",c='b',)#打开坐标网格
plt.show()plt.bar(x = range(1,26), # 指定条形图x轴的刻度值height=price[0],color = 'steelblue',width = 0.8)
plt.plot([1,26],[min_price,min_price],'g--')
plt.plot([1,26],[max_price,max_price],'r--')
plt.title('换电站的换电价格')
plt.ylabel('Price(￥)')
plt.axis([0,26,0,300])
# plt.grid(ls=":",c='b',)#打开坐标网格
plt.showindex = np.arange(1,26)
rects1 = plt.bar(index, e, 0.5, color='#0072BC')
rects2 = plt.bar(index + 0.5, E, 0.5, color='#ED1C24')
plt.axis([0,26,0,50])
plt.title('出租车的预期和实际数量')
plt.ylabel('E and e')
# plt.grid(ls=":",c='b',)#打开坐标网格
plt.xlabel('换电站')
plt.legend(['e','E'])
plt.show()