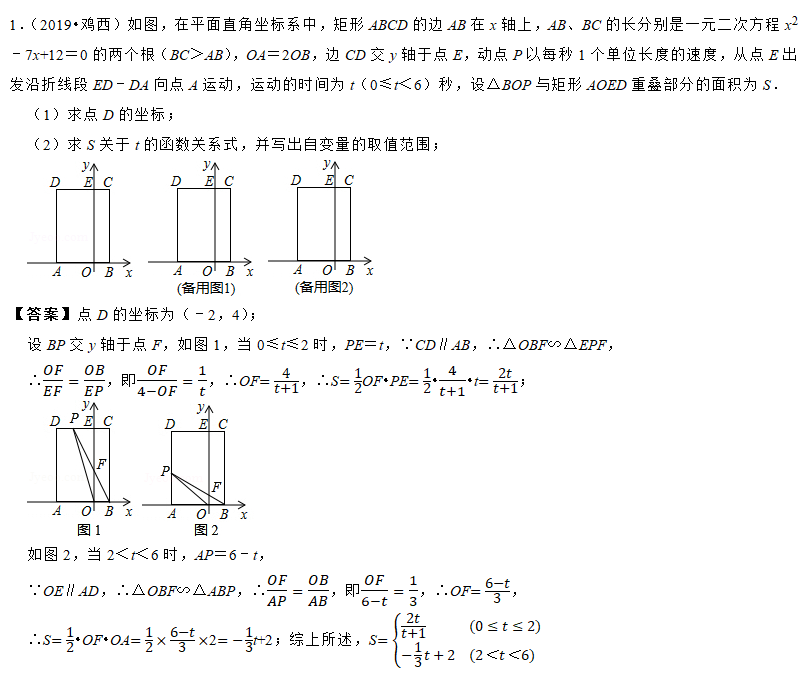
本文开始介绍重叠面积问题。

顾名思义，此类问题主要是求两个几何图形的重叠部分的面积。

解题的关键为画出图形，然后再表示面积。

文中的中考真题选自以下地区：

2019•资阳、2019•鸡西、2019黄冈

【题1】

(2019•资阳)在矩形ABCD中，连结AC，点E从点B出发，以每秒1个单位的速度沿着B→A→C的路径运动，运动时间为t(秒)．过点E作EF⊥BC于点F，在矩形ABCD的内部作正方形EFGH．

(1)如图，当AB＝BC＝8时，

①若点H在△ABC的内部，连结AH、CH，求证：AH＝CH；

②当0＜t≤8时，设正方形EFGH与△ABC的重叠部分面积为S，求S与t的函数关系式；

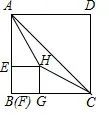
【分析】

本题的题目还是做了简化，只要求t不大于8时的重叠部分面积。

此时点E的运动范围为线段AB之间。

容易发现BE很小是，正方形EFGH再△ABC的内部，

重叠部分面积就是该图形。

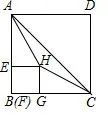
当点H在AC上时，此时BH⊥AC，也就是说点H为AC的中点，

易得点E为AB的中点，

当点E继续往上运动，此时会超出△ABC的范围，变成五边形，

使用割补法即可。

明白了吗？

【答案】

解：

如图1中，当0＜t≤4时，重叠部分是正方形EFGH，S＝t²．

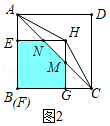
如图2中，当4＜t≤8时，重叠部分是五边形EFGMN，S＝S△ABC﹣S△AEN﹣S△CGM=1/2×8×8﹣2×1/2(8﹣t)²＝﹣t²+16t﹣32．

综上所述，

S=t²，(0＜t≤4)

S=-t²+16t-32，(4＜t≤8)．

【举一反三】