本文仅作为学习记录，欢迎各位提出宝贵建议
1、超前补偿环节的分数化
在上周我学习了分数阶RC的实现方式，无独有偶，超前补偿环节也可以应用插值的方式来近似分数阶补偿。
整数阶超前补偿的弊端主要有二：
一、当采样频率和固定频率的比值过小时，超前环节的分辨率太低，无法准确补偿相位延迟。
超前相位补偿器z^m在ω处的补偿角度θ为:
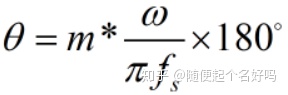
当m=1，ω=ω0时，θ最小，为：
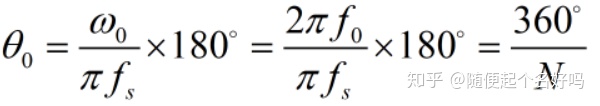
可以看出超前补偿器的分辨率仅由采样频率和固定频率的比值N决定，此时整数阶超前补偿无法满足补偿的精度
二、由于稳定性条件的约束，应用一些整数阶的超前环节的同时，可能无法使用较大的辅助控制器Q。
文献[1]中提到了超前环节与辅助控制器Q大小的关系，两者共同受到稳定性条件的制约。
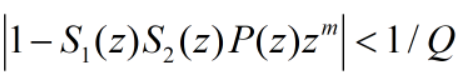
S1(z)为陷波器，S2(z)为低通滤波器，P(z)为LCL滤波器和逆变器的建模。上式是由RC控制系统的稳定性条件得出来的。令G(z)=S1(z)S2(z)P(z),画出左式曲线
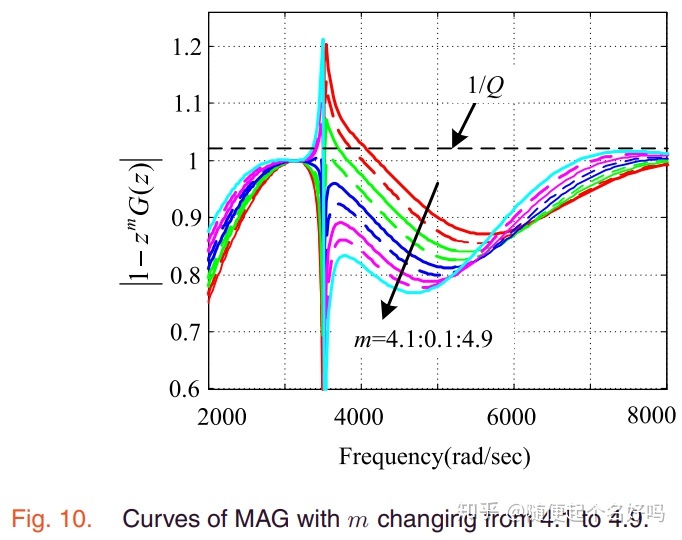
文献[1]设计Q=0.95，并在上图中画出，需要左式在低频处满足小于1/Q，才能保证系统稳定。m=4/5时峰值太大，无法满足较大的Q，应用分数后，当m=4.5时，可以满足Q=0.95的情况。文献[2]的实验证明，小数超前相位补偿可以使相位更接近与0°，使RC增益kr可以取到更大的值
所以，分数化的设计超前相位环节是比较有意义的，设计方法仍然是拉格朗日法插值多项式近似。d为超前环节小数部分，h(n)为拉格朗日系数。
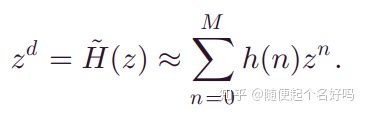
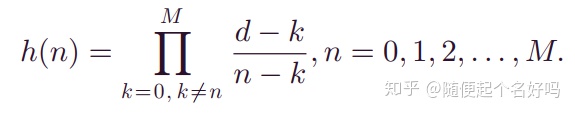
应用分数阶超前相位环节时，RC对谐波的抑制效果更好。文献[2]从无负载、线性负载和非线性负载三种情况下证明了这一点。
2、引入校正因子
基于插值法的近似计算运算量太大，文献[3]的作者提出可以使用校正因子来抵消由于延迟环节阶数四舍五入造成的误差。
并联选择谐波RC中加入校正因子：
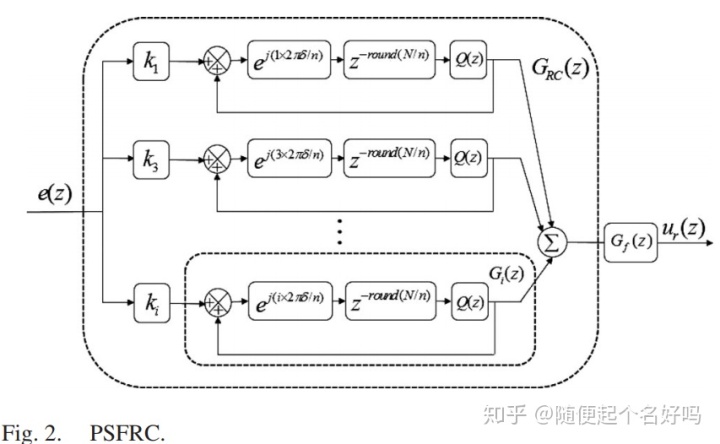
图图
图中的几个参数代表含义为：
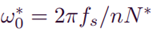
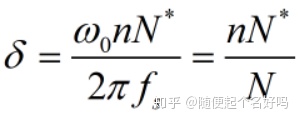
图中的δ是校正因子，改进后的RC中心频率变为：
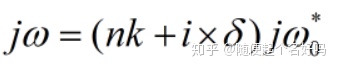
当N为整数时，δ=1，中心频率与平常无异；当N为分数时，中心频率有所偏移。
当采样频率与固定频率之比N向上取整时，基波及谐波频率稍微变大，为了防止控制器增益因此减小，所以利用校正因子将RC的中心频率均向上调整。
当采样频率与固定频率之比N向下取整时，基波及谐波频率稍微变小，为了防止控制器增益因此减小，所以利用校正因子将RC的中心频率均向下调整。
该方法与插值的不同之处在于：对于分数延时环节，直接对阶数取整，再通过校正因子对取整c造成的误差进行补偿。由于只需要对校正因子进行计算，大大减小了计算量。
——————————————平平无奇的分割线————————————————
2020.6.26补充
在看过文献[3]同作者前一年的文章文献[4]后，我对文献[3]中所提的校正因子理解更深刻了一些，所以做出一些补充记录。
还是从引入校正因子的并行结构nk±m阶RC的中心频率入手：
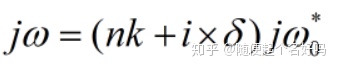
当N为整数时，δ=1，中心频率与平常无异；
当N为分数时，δ≠1，校正因子开始发挥作用：
当k=0时，
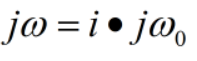
可见引入校正因子后，N为分数的情况下，在低次奇数次频率处，中心频率是准确的，未发生偏移。在此处的增益与N为整数的情况相同。
k≠0时，δ发挥校正作用；通过计算可知：
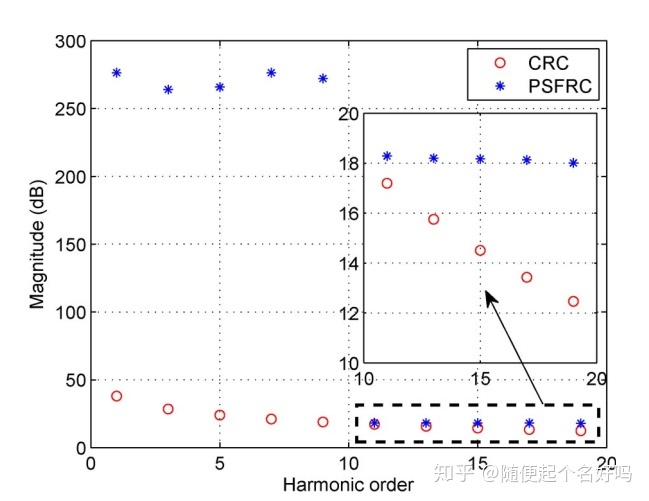
低次奇数次谐波才是控制中最主要的谐波。由上图可知，引入校正因子后，RC在低次奇数次谐波的增益非常高，对这些次数的谐波抑制效果明显。与此同时，在高次谐波的增益增加不明显，所以对于高次谐波，进行“选择性放弃”，直接用低通滤波器滤除高次谐波。
缺陷：
1、只有n倍频以下的奇数次谐波才有很好的谐波抑制效果。n取得很大时，才能尽可能的扩大抑制低次谐波的范围，但由于n的扩大，使得并联支路同时增加，系统结构变得更加复杂。给设计参数，系统的稳定带来一些挑战。
2、高次谐波的控制效果增加有限，需要截止频率较小的滤波器。
参考文献
[1]Q. S. Zhao and Y. Q. Ye. Fractional Phase Lead Compensation RC for an Inverter: Analysis, Design, and Verification[J]. IEEE Transactions on Industrial Electronics,2017, 64(4):3127-3136
[2]Z. C. Liu and Y. Q. Ye. Universal Fractional-Order Design of Linear Phase Lead Compensation Multirate Repetitive Control for PWM Inverters[J]. IEEE Transactions on Industrial Electronics,2017, 64(9):7132-7140
[3]T. Q. Liu and D. W. Wang. High-Performance Grid Simulator Using Parallel Structure Fractional Repetitive Control[J]. IEEE Transactions on Power Electronics,2016, 31(3):2669-2679
[4]T. Q. Liu and D. W. Wang. Parallel Structure Fractional Repetitive Control for PWM Inverters[J]. IEEE Transactions on Industrial Electronics,2015, 62(8):5045-5054
