sql相同顺序法和一次封锁法_数学专题

数学专题(一)

隔板法的妙用

浓度常见哪些问题?

排列组合分堆？涂色？到底掌握透彻了吗？

解析几何与韦达定理？

公式总是记不住？应用题还不会解？

除了写作(写作听我的)、逻辑(逻辑说)专题外，本周起我们也将隆重推出数学专题，恶补数学知识，让大家一看到题就能判断类型找出解题方法！感兴趣的小伙伴记得点个在看，感谢支持~

思维导图：

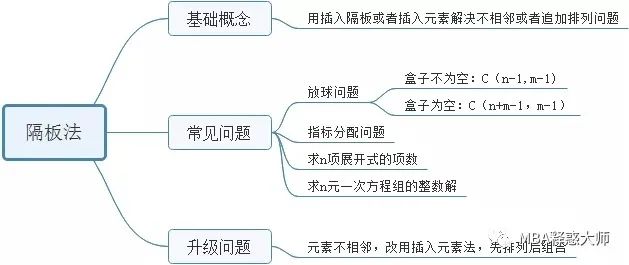
专题解析：

在组合数学中，隔板法(又叫插空法)是排列组合的推广，主要用于解决不相邻组合与追加排列的问题。

隔板法就是在n个元素间插入(b-1)个板，即把n个元素分成b组的方法。

不允许为空：对n件相同物品(或名额)分给m个人(或位置)，允许若干个人(或位置)不为空的问题,可以看成将这n件物品分成m组，允许若干组为空的问题.将n件物品分成m组，需要m-1块隔板，因隔板无差别，故隔板之间无序，是组合问题，故隔板有C^m-1_n-1。

允许为空：对n件相同物品(或名额)分给m个人(或位置)，允许若干个人(或位置)为空的问题,可以看成将这n件物品分成m组，允许若干组为空的问题.将n件物品分成m组，需要m-1块隔板，将这n件物品和m-1块隔板排成一排，占n+m-1位置，从这n+m-1个位置中选m-1个位置放隔板，因隔板无差别，故隔板之间无序，是组合问题，故隔板有C^m-1_n+m-1种不同的方法，再将物品放入其余位置，因物品相同无差别，故物品之间无顺序，是组合问题，只有1种放法，根据分步计数原理，共有C^m-1_n+m-1×1= C^m-1_n+m-1种排法。

例题解析：

一、放球问题

例1

把8个相同的球放入4个不同的盒子，有多少种不同的放法？( )

A.110 B.144 C.165 D.180 E.210

【解析】：取3块相同隔板，连同8个相同的小球排成一排，共11个位置。由隔板法知，在11个位置中任取3个位置排上隔板，共有C(11，3)种排法。所以，把个相同的球放入个不同的盒子，有种不同方法。故选C

例2

将20个大小形状完全相同的小球放入3个不同的盒子，允许有盒子为空，但球必须放完，有多少种不同的方法？( )

A.180 B.200 C.230 D.231 E.240

【解析】本题中的小球大小形状完全相同，故这些小球没有区别，问题等价于将小球分成三组，允许有若干组无元素，用隔板法。

将20个小球分成三组需要两块隔板，因为允许有盒子为空，不符合隔板法的原理，那就人为的再加上3个小球，保证每个盒子都至少分到一个小球，那就符合隔板法的要求了(分完后，再在每组中各去掉一个小球，即满足了题设的要求)。然后就变成待分小球总数为23个，球中间有22个空档，需要在这22个空档里加入2个隔板来分隔为3份，共有C(22，2)=231种不同的方法。故选D

例3

现有7个完全相同的小球，将它们全部放入编号为1，2，3，4的四个盒子中，每个盒子至少放一个球，问有多少种不同的放法？( )

A．6 B.20 C.35 D.48 E.以上答案均不正确

【解析】这道题满足隔板法基本模型的三大条件，所以我们可以直接应用隔板法。首先我们将7个小球排成一排。在7个小球中间一共有6个间隔，在这6个间隔中我们挑出3个间隔插入隔板，这样我们就将小球分成了四份，并且每一份都至少有一个小球。接着我们将这四份小球按从左到右的顺序依次放入1-4号四个盒子中，就得到了对应的一种放法。这样一来，每一种隔板的插法就对应了一种小球的方法。6个间隔中插入3个隔板的插法共有种C(6,3)=20，即本题共有20种不同的放法。

例4

现有8个完全相同的小球，将它们全部放入编号为1，2，3的三个盒子中，允许出现空盒，问有多少种不同的放法？

【解析】先加入3个球，加上原来地8个球，现在共有11个球，利用隔板法将它们放到三个盒子中，共有种C(10,2)=45种放法。对于每一种放法，然后都从每个盒子中拿出一个球，当盒中分到一个球之后还回1个球，该盒实际上是空盒；分到两个球后还回1个球，该盒实际上只含一个球，依此类推。这样就成功地将8个相同的小球分入了三个盒中，允许有空盒的共有45种放法。

二、指标分配问题

例1

某校召开学生会议，要10个学生代表名额，分配到某年级的6个班中，若每班至少1个名额，有多少种不同分法？

【解析】名额与名额是没有差别的，而班级与班级是有差别的，把相同的名额分配到个不同的班级，适合隔板法。分两步。第一步：个班每班先分配个名额，只有种分法；第二步：将剩下的个名额分配给个班。取块相同隔板，连同个相同名额排成一排，共个位置。由隔板法知，在个位置中任取个位置排上隔板，有种排法。由分步计数原理知：个学生代表名额，分配到某年级的个班中，每班至少个名额，共有种不同分法。

点评：名额与名额是没有差别的，而班级与班级是有差别的，所以适合隔板法。

三、求n项展开式的项数

例1

求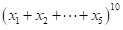展开式中共有多少项？

【解析】用个相同的小球代表幂指数10, 用5个标有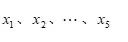

的5个不同的盒子表示数x1、x2、...、x5，将10个相同的小球放入5个不同的盒子中，把标有xi(i=1,2...5)的每个盒子得到的小球数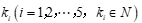，记作xi的ki次方。这样，将10个相同的小球放入5个不同的盒子中的每一种放法，就对应着展开式中的每一项。取5-1=4块相同隔板，连同10个相同的小球排成一排，共14个位置。由隔板法知，在14个位置中任取4个位置排上隔板，有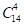种排法。故展开式共有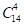=1001项。

四、求n元一次方程组的非负整数解

例1

求方程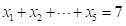的正整数解的个数。

【解析】用7个相同的小球代表数7, 用5个标有同上的个不同的盒子表示均不能为的正整数未知数同上。要得到方程的正整数解的个数，分两步。第一步：5个盒子每个盒子先分配1个小球，只有1种分法；第二步：将剩下的2个小球分配给5个盒子。取5-1=4块相同隔板，连同2个相同小球排成一排，共6个位置。由隔板法知，在6个位置中任取4个位置排上隔板，有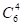种排法。由分步计数原理知：共有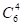种放法。我们把标有xi的每个盒子得到的小球数ki，记作：xi=ki。这样，将7个相同的小球放入5个不同的盒子中的每一种放法，就对应着方程的每一组解(k1,k2...k5)。所以，方程的正整数解共有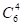=15个。