引言

数据压缩方面，我们往往可以通过稀疏数组来保存有效数据，节省存储空间。

一、稀疏数组的概念

当一个数组中大部分元素是0，或为同一个值的时候，可以使用稀疏数组来保存数组。

它是一个十分有效的存储结构，便于节省存储空间。

它的处理方式是：

1、记录数组一共有几行几列，有多少不同的值；

2、把具有不同值的元素的行、列及值记录在一个小规模二维数组中（稀疏数组），从而缩存储数据的规模。

二、稀疏数组的存储结构

稀疏数组实际上是一个典型的二维数组，它描述的是一个标准二维数组的有效数据，如果标准二维数组的内容如下所示的话：

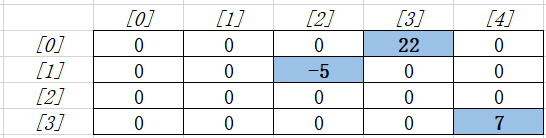
那么这个标准二维数组对应的稀疏数组的结构就如下图所示：

如上图所示。

稀疏数组有固定的三列，分别代表原始二维数组的行、列和值，但是第一行具有特殊的含义：稀疏数组的第一行存储原始数组的行数、列数和有效数据个数，这三个信息。而从第二行（也就是[1]行）开始，才是真正的原始二维数组的有效数据。

【扩展】稀疏数组可以描述二维数组，但同时，我认为它也可以描述更高维的数组，比如三维空间数组，那么相应稀疏数组结构也会有所变化。所以稀疏数组并不是只能描述一个二维数组，凡是可以只保存原始数组有效数据的都可以是稀疏数组，只不过二维数组对应的稀疏数组更有代表性。

三、五子棋盘的保存与复盘

五子棋可能没有几个人没玩过，那么在线上的五子棋游戏中，后台实际上并没有保存整个棋盘，而是利用稀疏数组保存有效数据，下面我们就看看如何通过Java 编写利用稀疏数组对五子棋局的保存与复盘吧。

3.1 五子棋盘的保存

假设在五子棋游戏中，数字1 代表黑子、2 代表白子，0 代表没有任何棋子，棋盘是一个可容纳 11 × 11 个棋子的正方形。黑子先行，双方都下了两步，形成了下面的局势：

public static void main(String[] args) {int[][] chessArr = new int[11][11];chessArr[1][2] = 1;chessArr[2][3] = 2;chessArr[1][4] = 1;chessArr[1][3] = 2;// 输出原始二维数组printArr(chessArr, "原始的二维数组······");
}

其中 printArr()是一个输出二维数组的静态工具方法：

/*** 输出二维数组数组工具方法*/
private static void printArr(int[][] arr, String msg) {System.out.println(msg);for (int[] row : arr) {for (int data : row) {System.out.printf("%d ", data);}System.out.println();}
}

那么这个11 × 11 的二维数组，根据上面介绍的稀疏数组的结构，进行保存，代码如下：

/*** 二维数组转稀疏数组* @param chessArr* @return*/
private static int[][] getSparseArr(int[][] chessArr) {// 将二维数组转为稀疏数组// 1、先遍历二维数组，得到非 0 数据的个数int sum = 0;// 二维数组的 length 取的是行数for (int i = 0; i < chessArr.length; i++) {for (int j = 0; j < chessArr[0].length; j++) {if (chessArr[i][j] != 0) {sum++;}}}
//		System.out.println("sum = " + sum);// 2. 创建对应的稀疏数组int[][] sparseArr = new int[sum + 1][3];// 给稀疏数组赋值sparseArr[0][0] = chessArr.length;sparseArr[0][1] = chessArr[0].length;sparseArr[0][2] = sum;// 将原始数组中的非 0 数据存放到稀疏数组中int sparseArrRow = 1;for (int i = 0; i < chessArr.length; i++) {for (int j = 0; j < chessArr[0].length; j++) {if (chessArr[i][j] != 0) {sparseArr[sparseArrRow][0] = i;sparseArr[sparseArrRow][1] = j;sparseArr[sparseArrRow][2] = chessArr[i][j];sparseArrRow++;}}}return sparseArr;
}

获得稀疏数组后输出：

int[][] sparseArr = getSparseArr(chessArr);
printArr(sparseArr, "输出稀疏数组······");

3.2 稀疏数组复盘五子棋

其实复盘的逻辑要更为简单，首先通过稀疏数组的第一行，初始化一个11 × 11 的二维数组，然后循环后面的行，取出每个数据放入到二维数组中去即可，代码如下：

/*** 复盘，稀疏数组转二维数组* @return*/
private static int[][] getReplayArr(int[][] sparseArr) {int[][] chessArr = new int[sparseArr[0][0]][sparseArr[0][1]];for (int i = 1; i < sparseArr.length; i++) {chessArr[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];}return chessArr;
}

通过上面的内容，我们重新复盘，并输出：

int[][] replayArr = getReplayArr(sparseArr);
printArr(replayArr, "复盘后的二维数组......");

可以看到，复盘后的棋盘与原始棋盘一模一样，这样就达到了利用稀疏数组节省存储空间的效果。

总结

稀疏数组总体来说还是比较简单的一个数据结构的利用，其中并未涉及任何算法，唯一的难点，可能就是二维数组转稀疏数组时的一些数组下标的思考和转化，不过通过画图也可以轻易地找出准确值。