java 最小生成树_图的最小生成树（java实现）

1.图的最小生成树(贪心算法)

我两个算法的输出都是数组表示的，当前的索引值和当前索引对应的数据就是通路，比如parent[2] = 5;即2和5之间有一个通路，第二个可能比较好理解，第一个有点混乱

是什么？

将一个有权图中的所有顶点都连接起来，并保证连接的边的总权重最小，即最小生成树，最小生成树不唯一

为什么？

传入邻接矩阵，返回可以生成最小生成树的数据

我们有两种方式生成图的最小生成树1.普里姆(Prim)算法2.克鲁斯卡尔(Kruskal)算法

怎样做？

下面是普里姆算法的最小生成树

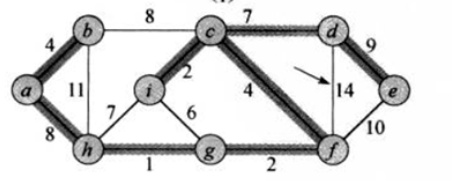
下面是克鲁斯卡尔算法的最小生成树：

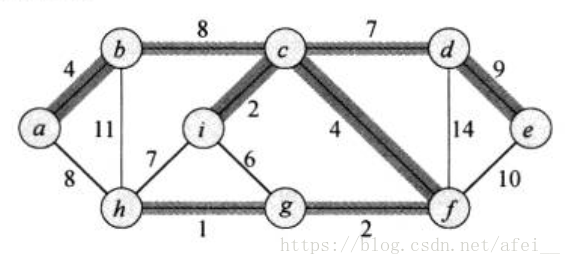
图的邻接矩阵表示法(无向图，上三角矩阵)

int[][] arr = new int[][]{

{-1, 4, 0, 0, 0, 0, 0, 8, 0},

{0, -1, 8, 0, 0, 0, 0, 11, 0},

{0, 0, -1, 7, 0, 4, 0, 0, 2},

{0, 0, 0, -1, 9, 14, 0, 0, 0},

{0, 0, 0, 0, -1, 10, 0, 0, 0},

{0, 0, 0, 0, 0, -1, 2, 0, 0},

{0, 0, 0, 0, 0, 0, -1, 1, 6},

{0, 0, 0, 0, 0, 0, 0, -1, 7},

{0, 0, 0, 0, 0, 0, 0, 0, -1}

};

1.普里姆算法(加点法)

需求：求出最小生成树的权值

输入参数：二维数组arr(邻接矩阵)，列表list(存放已经被加入的点)，整型sum(存放权值)

输出参数：整型数组parent

1)先找一个起点，这个起点为任意一点，放入list中2)如果list中不包含全部节点，进入循环1>遍历list中节点，查找不存在list中的邻接节点的最小值，记录下begin和end2>将begin和end放入数组中，较小值节点赋值给较大值所在数组位置

3)返回parent

实现：

importjava.util.ArrayList;importjava.util.Arrays;importjava.util.List;/*** 普里姆(Prim)算法

*@authorXiong YuSong

* 2019/3/22 16:02*/

public classPrim {public static voidmain(String[] args) {int[][] arr = new int[][]{

{-1, 4, 0, 0, 0, 0, 0, 8, 0},

{0, -1, 8, 0, 0, 0, 0, 11, 0},

{0, 0, -1, 7, 0, 4, 0, 0, 2},

{0, 0, 0, -1, 9, 14, 0, 0, 0},

{0, 0, 0, 0, -1, 10, 0, 0, 0},

{0, 0, 0, 0, 0, -1, 2, 0, 0},

{0, 0, 0, 0, 0, 0, -1, 1, 6},

{0, 0, 0, 0, 0, 0, 0, -1, 7},

{0, 0, 0, 0, 0, 0, 0, 0, -1}

};

List list = new ArrayList<>();//先将0放置在list中

list.add(0);int begin = 0, end = 0, weight;int[] parent = new int[arr.length];for (int i = 0; i < arr.length; i++) {

parent[i]= -1;

}while (list.size()

weight=Integer.MAX_VALUE;for(Integer row : list) {for (int i = 0; i < arr.length; i++) {if (!list.contains(i)) {if (i >= row + 1) {if (arr[row][i] > 0 && arr[row][i]

begin=row;

end=i;

weight=arr[row][i];

}

}else if (i <= row - 1) {//我这里只用了上三角矩阵，所以这里需要画蛇添足写这一部分

if (arr[i][row] > 0 && arr[i][row]

begin=row;

end=i;

weight=arr[i][row];

}

list.add(end);

parent[end]=begin;

}

System.out.println(Arrays.toString(parent));

}

2.克鲁斯卡尔算法(加边法)

需求：求出最小生成树的权值

构建类：Edge三元组，根据weight(权值)排序

输入参数：存放有Edge的列表list，并查集parent

输出参数：并查集parent(最小生成树的数组表现形式)

原理：贪心算法的实现，程序中使用了并查集(判断两个集合中是否存在相同的数据)这种特殊的数据结构，使用数组实现

1)创建一个三元组，将邻接矩阵中数据放入三元组中，再放入list中，根据权值进行排序2)创建变量count=0，整型数组parent3)如果list中还存在值，则进行循环1>判断begin和end是否存在于不同的集合中(判断是否在同一棵树中，即判断当前节点在并查集parent中的根节点是否为同一个)2>如果存在不同的集合中，则将较小值节点赋值给较大值所在数组位置，较小值节点为较大值节点的父节点4)返回parent

实现：

importjava.util.ArrayList;importjava.util.Arrays;importjava.util.Collections;importjava.util.List;/***@authorXiong YuSong

* 2019/3/22 17:04*/

class Edge implements Comparable{//起始点

private intbegin;//终止点

private intend;//权值

private intweight;public Edge(int begin, int end, intweight) {this.begin =begin;this.end =end;this.weight =weight;

}public intgetBegin() {returnbegin;

}public void setBegin(intbegin) {this.begin =begin;

}public intgetEnd() {returnend;

}public void setEnd(intend) {this.end =end;

}public intgetWeight() {returnweight;