现实生活中,我们只要掌握圆的周长和面积公式,了解球的表面积和体积公式就够用了,没有什么可以深究的。本篇将带你走进高维度球的表面积和体积公式[1]。
我们生活在三维空间,对更高维度的空间难以构想。笛卡尔说:我思故我在。借助一点点想象力,我们来推导一下n维球的体积公式。
以下都假设球的半径为r,表面积为S,体积为V。球心为坐标原点O,具有n个维度的点X坐标为
对于向量空间,距离测度分多种:
1范式 曼哈顿距离(Manhattan distance)
2范式 欧几里德距离(Euclidean distance)
n范式
超立方体
无穷大范式最简单,我们先作讨论。所有维度上的坐标的绝对值不超过r,这样的形状是一个边长为2r的超立方体。超(hyper,不是super)是一个泛化的概念,用以延伸到所有的维度上。
超立方体的各个轴都是正交的,所以体积
每个轴都有左右两个超平面限定,于是n维体有2n个面。在向高维扩展时,n维球的“体”就会沦落为n+1维球的“面”。我们有
超锥体
在曼哈顿距离下,
超球体
最后,我们来看一下常用的欧几里德距离——平方和后再开方。
先回忆一下公式:
圆的周长、面积公式
球的表面积、体积公式
根据上面的结论,一维球的“体”是二维球的“面”,对于一维球而言,其体积就是直线长度(类比二维球,即圆的周长),
关于圆的公式都涉及到
我们可以选取笛卡尔坐标系或极坐标系,笛卡尔坐标系下的式子比较繁琐。
转化成极坐标系,就是
从一个空间映射到另一个空间,或者从一个坐标系变换到另一个坐标系,需要乘以雅可比矩阵( Jacobi matrix )。
球是中心对称的,由n维球
基于被积函数是偶函数,缩小积分范围为
然后令
整理一下
积分是Beta函数形式,Beta函数的定义为
于是,
Beta函数与Gamma函数存在关系
Gamma函数的定义
到这里就是常见的一类积分了,同济大学高等数学教材有讲过高斯分布。平方后转换成平面直角坐标系二重积分,然后转换成极坐标系求解,用这样巧妙的方法得到
带入常数
通过一系列的迭代,Gamma函数分子分母相消,
带入
很显然有
三角函数积分
由于
换元,设
你也可以
好了,这一节的主角登场了。求积分
n取1或2时容易求解,这引导着我们用分部积分法(integration by parts )
带入
得到递推公式
接着,限定下上限分别为0和
如何体面
球可以由半径逐渐递增的壳来填充,类似俄罗斯套娃。当填充的壳的厚度趋近于0时,我们就得到球的体积。由于球、球面的各向同性,球面上任何一个微元(facet)都可以近似看成平面,其体积为
通过求导,我们很体面地从“体”计算出“面”。(no pun intended)
其实,体积与面积之间还存在这样一个比例关系
公式细究
Γ函数有很多的性质,是符合整数点阶乘运算的最佳连续函数。
当
当
当
有了公式之后,任意维度的体积[3]就可以轻松计算了。
对于n维单位球,我们用matplotlib画一下体积V关于维度n的函数图。
#!/usr/bin/env python3
import matplotlib
import numpy as np
import scipyimport matplotlib.pyplot as pltfrom scipy.special import gamma# For unit sphere of dimension n, the volume is
# V_n = frac {pi^{frac n 2}} {Gamma(frac n 2 + 1)}
t0 = -5.0
t1 = 20.0
t = np.arange(t0, t1, 0.1)
V = np.pi ** (t / 2.0) / gamma(t / 2.0 + 1.0)n = np.arange(t0, t1, 1.0)
V_n = np.pi ** (n / 2.0) / gamma(n / 2.0 + 1.0)figure, ax = plt.subplots()
ax.plot(t, V)
ax.plot(n, V_n, color='green', marker='o', linestyle='')ax.set_xlabel('n (dimensionality)')
ax.set_ylabel('C_n m^n')
ax.set_title('volume of n dimensional unit sphere')
ax.grid()figure.savefig("volume.png")
plt.show()需要安装numpy, scipy, matplotlib这三个Python库,没安装的可以安装一下,以后科学计算和作图用得到的。控制台下输入命令 pip3 install numpy, scipy, matplotlib。代码运行无误后,得到图:

上面顺带也画出了负维空间的情况。从正整数维度到分数维度,再到负数维度,一直扩充到了实数范围。从图中看到,对于单位球,五维空间的体积最大。五维空间是什么概念?不清楚。克里斯托弗·诺兰是一个商业和艺术结合最好的导演,他在电影《星际穿越》中向我们描述了一个五维空间的存在。
固定半径r,我们可以看到,随着n的增长,分母以越来越大的正整数增加,分子以系数
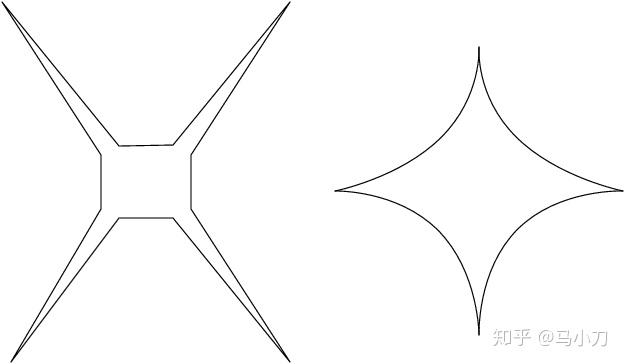
维度越高,越靠近坐标轴。很形象的一个比喻就是海胆,核越来越小,刺突越来越长,也越来越尖。想看动画效果?可以观察
参考
- ^Volume of an n-ball https://en.wikipedia.org/wiki/Volume_of_an_n-ball
- ^The Volume of a Hyperpyramid http://physicsinsights.org/pyramids-1.html
- ^Gamma Function and the Volumes of High Dimensional Spheres http://www.cs.nthu.edu.tw/~cchen/ISA5230/2017/sphere.pdf
- ^curse of dimensionality http://en.wikipedia.org/wiki/Curse_of_dimensionality

...)

















