1、前言
回顾前面几期的内容，在第一期中介绍了机器人的正/逆运动学建模，正运动学解决的问题是如何从关节空间的关节变量描述操作空间的位姿，反之则是逆运动学的内容。将操作空间和关节的空间的关系用以下关系式进行表达。
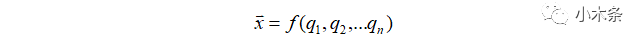
机器人正/逆运动学始终在解决上面这个公式，已知末端的位姿，求解关节变量，或者已知关节变量，确定末端的位姿，这些描述的是静态位置之间的关系，属于静态运动学问题。
在第二、三期介绍了机器人动力学建模，使用是拉格朗日法，由于需要计算的每个连杆的动能，因此在第三期介绍了角速度和线速度的传递公式，即在已知每个关节的转动/平动速度情况下，从第一个运动关节出发，递推末端关节的速度(v,w)。在本期中将介绍如在已知末端的速度的情况下，求得每个关节需要的运动速度。在机器人的控制方案，一般先规划末端的轨迹，而不是规划每个关节的运动速度，因此通过末端的运动状态求解关节的运动更具现实意义。
2、雅克比矩阵
2.1概念补充
关节空间：n个自由度的机械臂的末端位姿由n个关节变量决定，这n个关节变量统称为n维关节矢量，所有关节矢量构成的空间称为关节空间。即关节空间是由关节变量组成的空间。
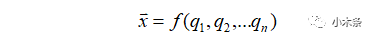
式中指右边部分
操作空间：也称任务空间，一般来讲是笛卡尔空间，简单来讲就是空间直角坐标系。末端的位姿在这个空间描述，上式指左边部分。关于末端空间姿态的表示的方法后续补充。
矩阵的求导：这里直接给出矩阵的求导的计算公式。
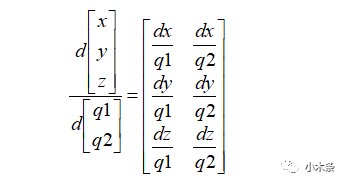
2.2雅克比矩阵意义
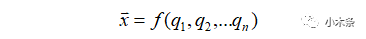
在前面我们知道正/逆运动学所要做的内容，可以用上式进行表述，那么是否存在这个的表达式能够将操作空间的速度和关节空间的速度联系起来。首先对上式关于时间t进行求导
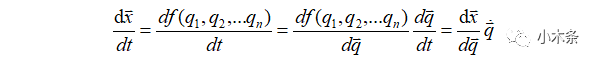
通过链式法则得到了操作空间的速度与关节空间的速度关系，将以上关系简记成如下形式：
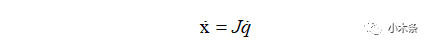
其中J即为本期需要介绍的雅克比矩阵，它建立从关节变量速度到末端速度的映射，且它们之间的关系为线性的。
2.3雅克比矩阵计算
方法一：根据变换矩阵
在笛卡尔坐标系下，末端的位姿和速度表示如下：
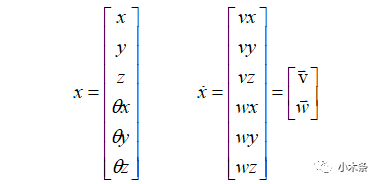
那么雅克比矩阵相应的可以表示成：
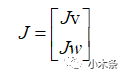
线速度部分
可以根据变换矩阵，其中第四列代表的含义为末端的位置。将第四列的前三个提取出来关于关节变量进行求导即可。
角速度部分
末端角速度是由每个不同的旋转关节进行线性叠加而成，在三维空间中，角速度的表示为指向旋转轴的向量，其方向可借助右手定则进行判断。在以自身旋转轴旋转和关节自身的坐标系下考虑角速度对末端的影响，关节的旋转轴在自身坐标系下通常定义为z轴([0,0,1])，角速度定义为[0,0,w],那么对于末端的角速度的贡献为[0,0,w]([0,0,1].*w)。而Jw是基于基坐标系下的表述形式。因此只需要将每个旋转轴转换成基坐标系中表示即可。
方法二：微元法
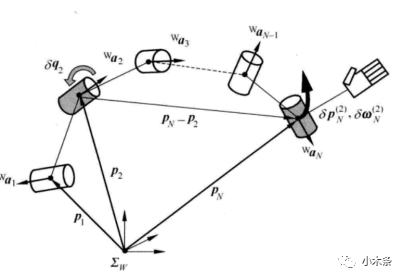
假设其它关节不动，只有第二关节绕其轴旋转微小角度。由此产生的第N个连杆的微小位移和微小转动。
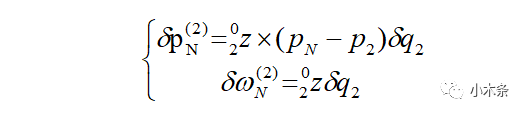
写成矩阵的形式：
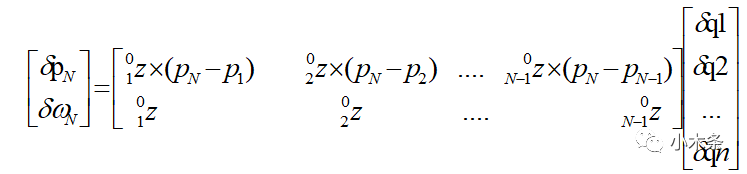
其中：
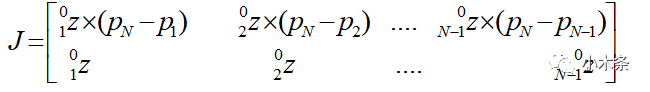
方法三：根据速度传递公式
速度的传递公式可回顾第三期的内容。这里直接写出速度的传递公式：
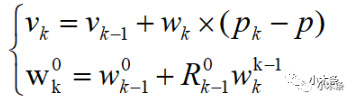
以上均针对转动关节而言，将雅克比矩阵写成以下形式：
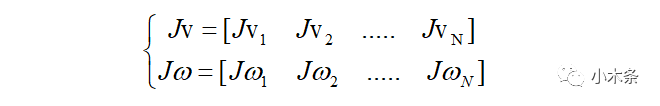
对于末端的线速度记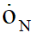
，末端角速度记为we,末端的速度是由每个关节运动对末端叠加，
写出如下叠加公式：
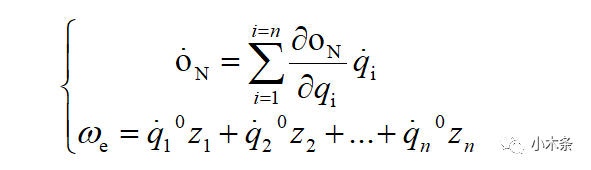
其中：
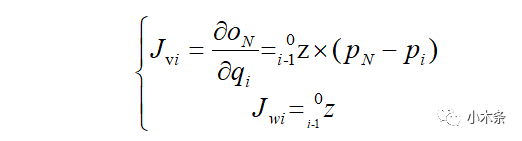
同上写出：
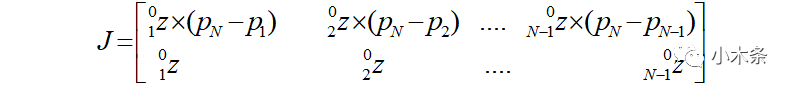
【下期预告】
实例讲解雅克比矩阵(下)-----雅克比应用
