推荐阅读:
- 面试BAT 却被小小字符串秒杀?这13道题帮你一举击败字符串算法题
- 字节跳动秋招面经:后端开发工程师,已拿意向书
前言
平时的编码中,我们经常需要判断两个文本的相似性,不管是用来做文本纠错或者去重等等,那么我们应该以什么维度来判断相似性呢?这些算法又怎么实现呢?这篇文章对常见的计算方式做一个记录。

Jaccard 相似度
首先是 Jaccard 相似度系数,下面是它在维基百科上的一个定义及计算公式。
The Jaccard index, also known as Intersection over Union and the Jaccard similarity coefficient (originally given the French name coefficient de communauté by Paul Jaccard), is a statistic used for gauging the similarity and diversity of sample sets. The Jaccard coefficient measures similarity between finite sample sets, and is defined as the size of the intersection divided by the size of the union of the sample sets:
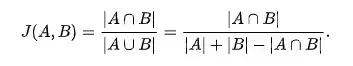
其实总结就是一句话:集合的交集与集合的并集的比例.
java 代码实现如下:
public static float jaccard(String a, String b) { if (a == null && b == null) { return 1f; } // 都为空相似度为 1 if (a == null || b == null) { return 0f; } Set aChar = a.chars().boxed().collect(Collectors.toSet()); Set bChar = b.chars().boxed().collect(Collectors.toSet()); // 交集数量 int intersection = SetUtils.intersection(aChar, bChar).size(); if (intersection == 0) return 0; // 并集数量 int union = SetUtils.union(aChar, bChar).size(); return ((float) intersection) / (float)union; }Sorensen Dice 相似度系数
与 Jaccard 类似,Dice 系数也是一种计算简单集合之间相似度的一种计算方式。与 Jaccard 不同的是,计算方式略有不同。下面是它的定义。
The Sørensen–Dice coefficient (see below for other names) is a statistic used to gauge the similarity of two samples. It was independently developed by the botanists Thorvald Sørensen[1] and Lee Raymond Dice,[2] who published in 1948 and 1945 respectively.
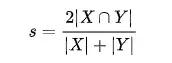
需要注意的是,他是:集合交集的 2 倍除以两个集合相加。并不是并集.
java 代码实现如下:
public static float SorensenDice(String a, String b) { if (a == null && b == null) { return 1f; } if (a == null || b == null) { return 0F; } Set aChars = a.chars().boxed().collect(Collectors.toSet()); Set bChars = b.chars().boxed().collect(Collectors.toSet()); // 求交集数量 int intersect = SetUtils.intersection(aChars, bChars).size(); if (intersect == 0) { return 0F; } // 全集,两个集合直接加起来 int aSize = aChars.size(); int bSize = bChars.size(); return (2 * (float) intersect) / ((float) (aSize + bSize)); }Levenshtein
莱文斯坦距离,又称 Levenshtein 距离,是编辑距离的一种。指两个字串之间,由一个转成另一个所需的最少编辑操作次数。
简单的说,就是用编辑距离表示字符串相似度, 编辑距离越小,字符串越相似。
java 实现代码如下:
public static float Levenshtein(String a, String b) { if (a == null && b == null) { return 1f; } if (a == null || b == null) { return 0F; } int editDistance = editDis(a, b); return 1 - ((float) editDistance / Math.max(a.length(), b.length())); } private static int editDis(String a, String b) { int aLen = a.length(); int bLen = b.length(); if (aLen == 0) return aLen; if (bLen == 0) return bLen; int[][] v = new int[aLen + 1][bLen + 1]; for (int i = 0; i <= aLen; ++i) { for (int j = 0; j <= bLen; ++j) { if (i == 0) { v[i][j] = j; } else if (j == 0) { v[i][j] = i; } else if (a.charAt(i - 1) == b.charAt(j - 1)) { v[i][j] = v[i - 1][j - 1]; } else { v[i][j] = 1 + Math.min(v[i - 1][j - 1], Math.min(v[i][j - 1], v[i - 1][j])); } } } return v[aLen][bLen]; }代码中的编辑距离求解使用了经典的动态规划求解法。
我们使用了** 1 - ( 编辑距离 / 两个字符串的最大长度) ** 来表示相似度,这样可以得到符合我们语义的相似度。
汉明距离
汉明距离是编辑距离中的一个特殊情况,仅用来计算两个等长字符串中不一致的字符个数。
因此汉明距离不用考虑添加及删除,只需要对比不同即可,所以实现比较简单。
我们可以用similarity=汉明距离/长度来表示两个字符串的相似度。
java 代码如下:
public static float hamming(String a, String b) { if (a == null || b == null) { return 0f; } if (a.length() != b.length()) { return 0f; } int disCount = 0; for (int i = 0; i < a.length(); i++) { if (a.charAt(i) != b.charAt(i)) { disCount++; } } return (float) disCount / (float) a.length(); }下面是测试用例:
Assert.assertEquals(0.0f, StringSimilarity.hamming("java 开发










...)



)



