- 一 BP神经网络实现不使用MATLAB神经网络工具箱
- 问题
- 分析
- MATLAB实现代码
- 运行结果
- 绘制的图像
- 二 使用MATLAB的神经网络工具箱简易实现BP网络
- 问题
- 分析
- 工具箱中的相关函数一些参考了MATLAB自带的英文手册
- mapminmax函数
- newff函数新版本
- 关于nettrainParam的常用属性
- train函数
- sim函数
- MATLAB实现代码
- 运行结果
- 绘制的图像
-
一. BP神经网络实现(不使用MATLAB神经网络工具箱)
1. 问题
公路运量主要包括公路客运量和公路货运量两方面。某个地区的公路运量主要与该地区的人数、机动车数量和公路面积有关,已知该地区20年(1990-2009)的公路运量相关数据如下:
人数/万人
20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63
机动车数量/万辆
0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6 2.7 2.85 2.95 3.1
公路面积/单位:万平方公里
0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 0.56 0.59 0.59 0.67 0.69 0.79
公路客运量/万人
5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 22598 25107 33442 36836 40548 42927 43462
公路货运量/万吨
1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 13320 16762 18673 20724 20803 21804
2. 分析
样本数据较多,且已知影响数据的因素(三大因素:该地区的人数、机动车数量和公路面积),可考虑将其作为BP神经网络的训练集,对该神经网络进行训练,然后对训练好的神经网络进行测试,最后使用测试合格的神经网络进行预测工作。
3. MATLAB实现代码
BP_road.m
numberOfSample = 20; %输入样本数量 %取测试样本数量等于输入(训练集)样本数量,因为输入样本(训练集)容量较少,否则一般必须用新鲜数据进行测试 numberOfTestSample = 20; numberOfForcastSample = 2; numberOfHiddenNeure = 8; inputDimension = 3; outputDimension = 2;%准备好训练集%人数(单位:万人) numberOfPeople=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63]; %机动车数(单位:万辆) numberOfAutomobile=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6 2.7 2.85 2.95 3.1]; %公路面积(单位:万平方公里) roadArea=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 0.56 0.59 0.59 0.67 0.69 0.79]; %公路客运量(单位:万人) passengerVolume = [5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 22598 25107 33442 36836 40548 42927 43462]; %公路货运量(单位:万吨) freightVolume = [1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 13320 16762 18673 20724 20803 21804];%由系统时钟种子产生随机数 rand('state', sum(100*clock));%输入数据矩阵 input = [numberOfPeople; numberOfAutomobile; roadArea]; %目标(输出)数据矩阵 output = [passengerVolume; freightVolume];%对训练集中的输入数据矩阵和目标数据矩阵进行归一化处理 [sampleInput, minp, maxp, tmp, mint, maxt] = premnmx(input, output);%噪声强度 noiseIntensity = 0.01; %利用正态分布产生噪声 noise = noiseIntensity * randn(outputDimension, numberOfSample); %给样本输出矩阵tmp添加噪声,防止网络过度拟合 sampleOutput = tmp + noise;%取测试样本输入(输出)与输入样本相同,因为输入样本(训练集)容量较少,否则一般必须用新鲜数据进行测试 testSampleInput = sampleInput; testSampleOutput = sampleOutput;%最大训练次数 maxEpochs = 50000;%网络的学习速率 learningRate = 0.035;%训练网络所要达到的目标误差 error0 = 0.65*10^(-3);%初始化输入层与隐含层之间的权值 W1 = 0.5 * rand(numberOfHiddenNeure, inputDimension) - 0.1; %初始化输入层与隐含层之间的阈值 B1 = 0.5 * rand(numberOfHiddenNeure, 1) - 0.1; %初始化输出层与隐含层之间的权值 W2 = 0.5 * rand(outputDimension, numberOfHiddenNeure) - 0.1; %初始化输出层与隐含层之间的阈值 B2 = 0.5 * rand(outputDimension, 1) - 0.1;%保存能量函数(误差平方和)的历史记录 errorHistory = [];for i = 1:maxEpochs%隐含层输出hiddenOutput = logsig(W1 * sampleInput + repmat(B1, 1, numberOfSample));%输出层输出networkOutput = W2 * hiddenOutput + repmat(B2, 1, numberOfSample);%实际输出与网络输出之差error = sampleOutput - networkOutput;%计算能量函数(误差平方和)E = sumsqr(error);errorHistory = [errorHistory E];if E < error0break;end%以下依据能量函数的负梯度下降原理对权值和阈值进行调整delta2 = error;delta1 = W2' * delta2.*hiddenOutput.*(1 - hiddenOutput);dW2 = delta2 * hiddenOutput';dB2 = delta2 * ones(numberOfSample, 1);dW1 = delta1 * sampleInput';dB1 = delta1 * ones(numberOfSample, 1);W2 = W2 + learningRate * dW2;B2 = B2 + learningRate * dB2;W1 = W1 + learningRate * dW1;B1 = B1 + learningRate * dB1; end%下面对已经训练好的网络进行(仿真)测试%对测试样本进行处理 testHiddenOutput = logsig(W1 * testSampleInput + repmat(B1, 1, numberOfTestSample)); testNetworkOutput = W2 * testHiddenOutput + repmat(B2, 1, numberOfTestSample); %还原网络输出层的结果(反归一化) a = postmnmx(testNetworkOutput, mint, maxt);%绘制测试样本神经网络输出和实际样本输出的对比图(figure(1))-------------------------------------- t = 1990:2009;%测试样本网络输出客运量 a1 = a(1,:); %测试样本网络输出货运量 a2 = a(2,:);figure(1); subplot(2, 1, 1); plot(t, a1, 'ro', t, passengerVolume, 'b+'); legend('网络输出客运量', '实际客运量'); xlabel('年份'); ylabel('客运量/万人'); title('神经网络客运量学习与测试对比图'); grid on;subplot(2, 1, 2); plot(t, a2, 'ro', t, freightVolume, 'b+'); legend('网络输出货运量', '实际货运量'); xlabel('年份'); ylabel('货运量/万吨'); title('神经网络货运量学习与测试对比图'); grid on;%使用训练好的神经网络对新输入数据进行预测%新输入数据(2010年和2011年的相关数据) newInput = [73.39 75.55; 3.9635 4.0975; 0.9880 1.0268]; %利用原始输入数据(训练集的输入数据)的归一化参数对新输入数据进行归一化 newInput = tramnmx(newInput, minp, maxp);newHiddenOutput = logsig(W1 * newInput + repmat(B1, 1, numberOfForcastSample)); newOutput = W2 * newHiddenOutput + repmat(B2, 1, numberOfForcastSample); newOutput = postmnmx(newOutput, mint, maxt);disp('预测2010和2011年的公路客运量分别为(单位:万人):'); newOutput(1,:) disp('预测2010和2011年的公路货运量分别为(单位:万吨):'); newOutput(2,:)%在figure(1)的基础上绘制2010和2011年的预测情况------------------------------------------------- figure(2); t1 = 1990:2011;subplot(2, 1, 1); plot(t1, [a1 newOutput(1,:)], 'ro', t, passengerVolume, 'b+'); legend('网络输出客运量', '实际客运量'); xlabel('年份'); ylabel('客运量/万人'); title('神经网络客运量学习与测试对比图(添加了预测数据)'); grid on;subplot(2, 1, 2); plot(t1, [a2 newOutput(2,:)], 'ro', t, freightVolume, 'b+'); legend('网络输出货运量', '实际货运量'); xlabel('年份'); ylabel('货运量/万吨'); title('神经网络货运量学习与测试对比图(添加了预测数据)'); grid on;%观察能量函数(误差平方和)在训练神经网络过程中的变化情况------------------------------------------ figure(3);n = length(errorHistory); t3 = 1:n; plot(t3, errorHistory, 'r-');%为了更加清楚地观察出能量函数值的变化情况,这里我只绘制前100次的训练情况 xlim([1 100]); xlabel('训练过程'); ylabel('能量函数值'); title('能量函数(误差平方和)在训练神经网络过程中的变化图'); grid on;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
4. 运行结果
预测2010和2011年的公路客运量分别为(单位:万人):
ans =
1.0e+04 *
4.6188 4.6601
预测2010和2011年的公路货运量分别为(单位:万吨):
ans =
1.0e+04 *
2.1521 2.1519
5. 绘制的图像
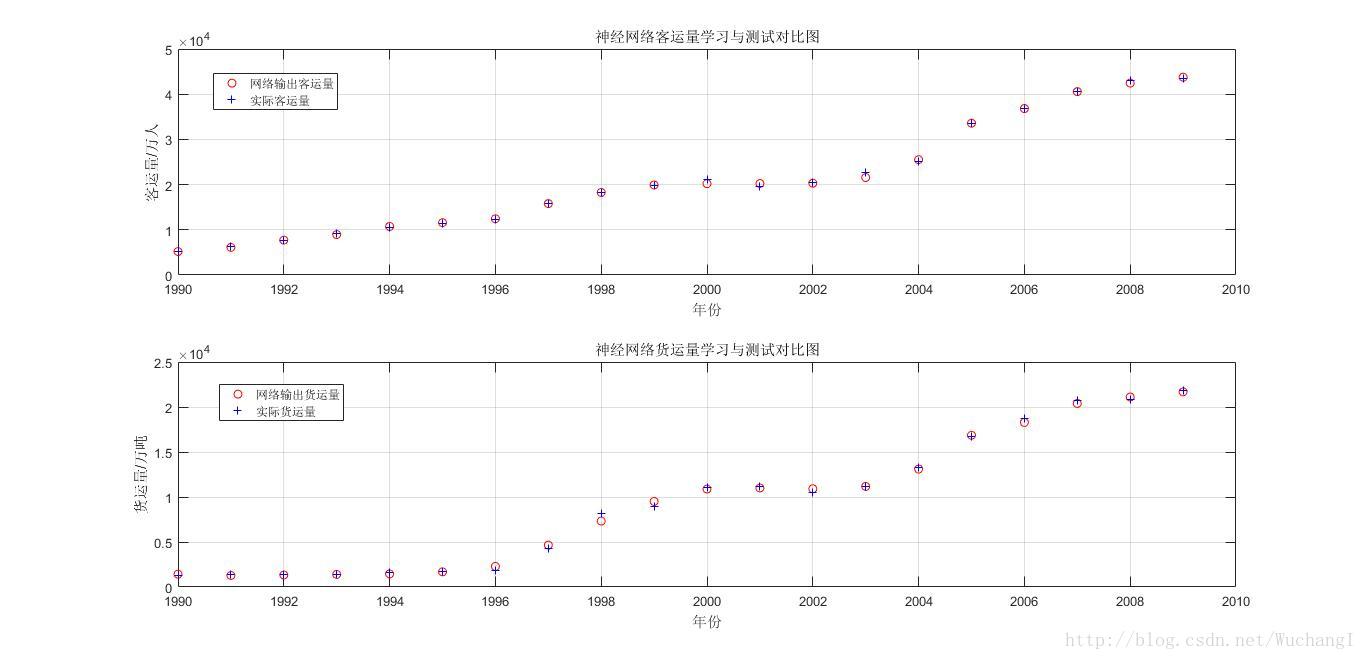
- figure(1)
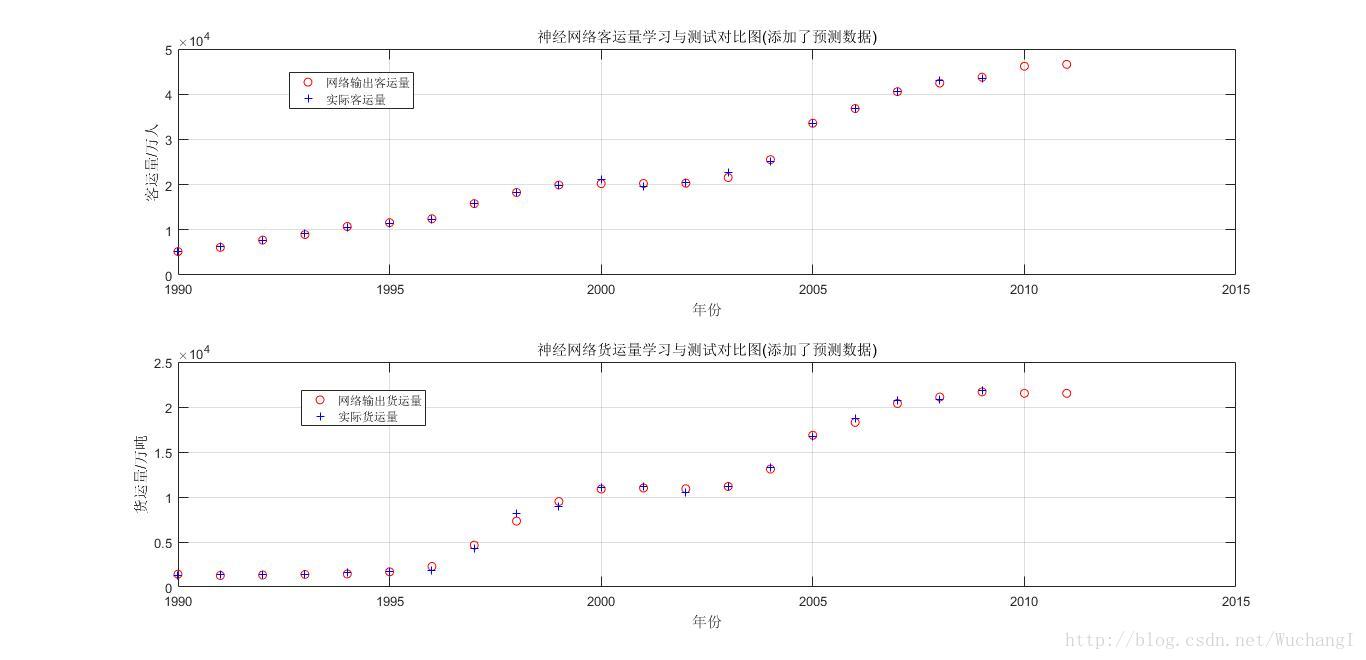
2. figure(2)
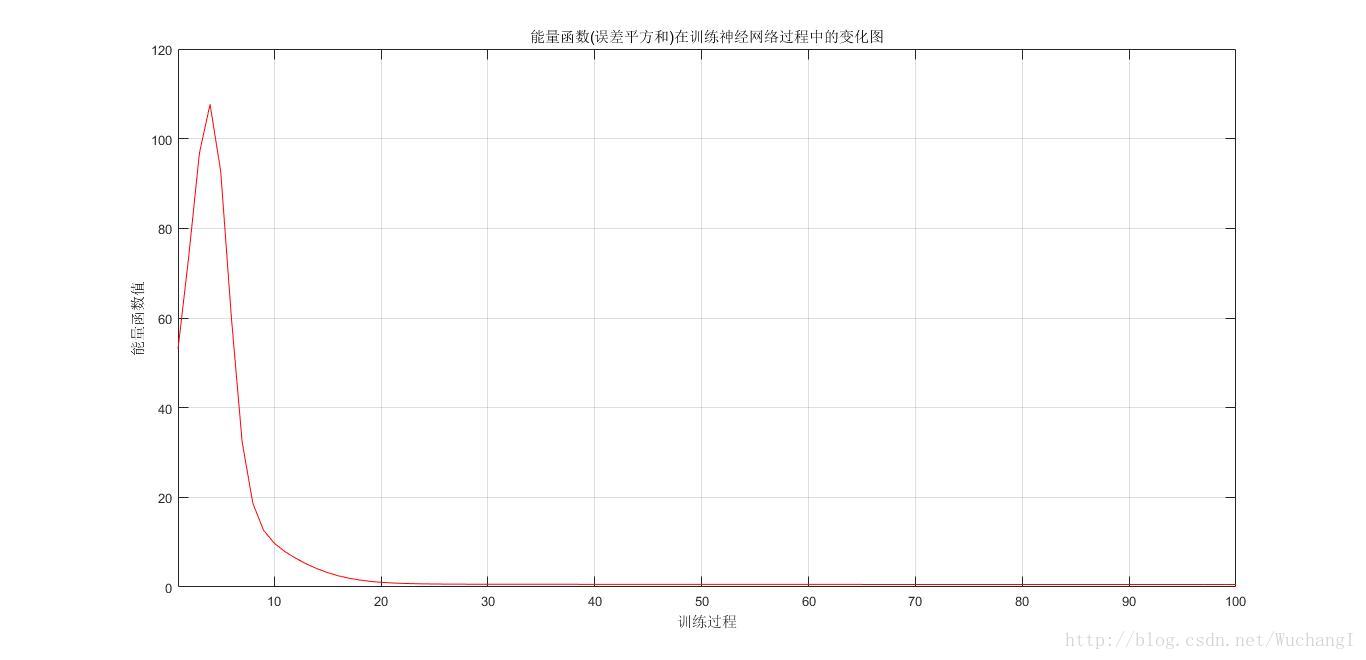
3. figure(3)
可以看出,使用BP网络中的负梯度下降原理之后,效果显著。
二. 使用MATLAB的神经网络工具箱简易实现BP网络
1. 问题
同<一>
2. 分析
同<一>
3. 工具箱中的相关函数(一些参考了MATLAB自带的英文手册)
mapminmax函数
- 功能:通过将原矩阵每行的最小值和最大值映射到[YMIN,YMAX]来得到规范化的矩阵。
- 算法:y = ( ymax - ymin ) * ( x - xmin ) / ( xmax - xmin ) + ymin
(注:当xmax与xmin相等时,则对原矩阵使用mapminmax函数仍得到原矩阵)
- 默认算法:
(默认情况下,mapminmax函数的YMIN和YMAX分别是-1和1)
y = 2 * ( x - xmin ) / ( xmax - xmin ) - 1
[Y,PS] = mapminmax(X)
- X:原矩阵
- Y:对矩阵X进行规范化得到的矩阵
- PS:存放关于原矩阵规范化过程中的相关映射数据的结构体
[Y,PS] = mapminmax(X,FP)
X:原矩阵
FP:含有字段FP.ymin和FP.ymax的结构体
Y:对矩阵X进行规范化得到的矩阵(使用在FP的ymin和ymax规定下的算法)
PS:存放关于原矩阵规范化过程中的相关映射数据的结构体
Y = mapminmax(‘apply’,X,PS)
- ’apply’:必写
- X:原矩阵
- PS:存放关于某个矩阵规范化过程中的相关映射数据的结构体
- Y:对矩阵X进行规范化得到的矩阵(使用PS中的规范化方式)
X = mapminmax(‘reverse’,Y,PS)
- ’reverse’:必写
- Y:某个矩阵
- PS:存放关于某个矩阵规范化过程中的相关映射数据的结构体
- X:将矩阵Y反规范化得到的矩阵(使用PS中的规范化方式,这里指将矩阵X转换为矩阵Y的规范化方式)
newff函数(新版本)
a. 功能:建立一个前馈反向传播(BP)网络。
b. net=newff(P,T,S)
- P: 输入数据矩阵。(RxQ1),其中Q1代表R元的输入向量。其数据意义是矩阵P有Q1列,每一列都是一个样本,而每个样本有R个属性(特征)。一般矩阵P需要事先归一化好,即P的每一行都归一化到[0 1]或者[-1 1]。
- T:目标数据矩阵。(SNxQ2),其中Q2代表SN元的目标向量。数据意义参考上面,矩阵T也是事先归一化好的。
- S:第i层的神经元个数。(新版本中可以省略输出层的神经元个数不写,因为输出层的神经元个数已经取决于T)
c. net = newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF)(提供了可选择的参数)
- TF:相关层的传递函数,默认隐含层使用tansig函数,输出层使用purelin函数。
- BTF:BP神经网络学习训练函数,默认值为trainlm函数。
- BLF:权重学习函数,默认值为learngdm。
- PF:性能函数,默认值为mse。
- PF,OPF,DDF均为默认值即可。
d. 常用的传递函数:
- purelin:线性传递函数
- tansig:正切 S 型传递函数
- logsig: 对数 S 型传递函数
(注意:隐含层和输出层函数的选择对BP神经网络预测精度有较大影响,一般隐含层节点传递函数选用tansig函数或logsig函数,输出层节点转移函数选用tansig函数或purelin函数。)
关于net.trainParam的常用属性
(假定已经定义了一个BP网络net)
* net.trainParam.show: 两次显示之间的训练次数
* net.trainParam.epochs: 最大训练次数
* net.trainParam.lr: 网络的学习速率
* net.trainParam.goal: 训练网络所要达到的目标误差
* net.trainParam.time: 最长训练时间(秒)train函数
功能:训练一个神经网络
[NET2,TR] = train(NET1,X,T)(也可[NET2] = train(NET1,X,T) )
- NET1:待训练的网络
- X: 输入数据矩阵(已归一化)
- T:目标数据矩阵(已归一化)
- NET2:训练得到的网络TR:存放有关训练过程的数据的结构体
sim函数
功能:模拟Simulink模型
SimOut = sim(‘MODEL’, PARAMETERS)
- (见名知意,不必再解释)
4. MATLAB实现代码
BP_toolbox_road.m
%准备好训练集%人数(单位:万人) numberOfPeople=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63]; %机动车数(单位:万辆) numberOfAutomobile=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6 2.7 2.85 2.95 3.1]; %公路面积(单位:万平方公里) roadArea=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 0.56 0.59 0.59 0.67 0.69 0.79]; %公路客运量(单位:万人) passengerVolume = [5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 22598 25107 33442 36836 40548 42927 43462]; %公路货运量(单位:万吨) freightVolume = [1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 13320 16762 18673 20724 20803 21804];%输入数据矩阵 p = [numberOfPeople; numberOfAutomobile; roadArea]; %目标(输出)数据矩阵 t = [passengerVolume; freightVolume];%对训练集中的输入数据矩阵和目标数据矩阵进行归一化处理 [pn, inputStr] = mapminmax(p); [tn, outputStr] = mapminmax(t);%建立BP神经网络 net = newff(pn, tn, [3 7 2], {'purelin', 'logsig', 'purelin'});%每10轮回显示一次结果 net.trainParam.show = 10;%最大训练次数 net.trainParam.epochs = 5000;%网络的学习速率 net.trainParam.lr = 0.05;%训练网络所要达到的目标误差 net.trainParam.goal = 0.65 * 10^(-3);%网络误差如果连续6次迭代都没变化,则matlab会默认终止训练。为了让程序继续运行,用以下命令取消这条设置 net.divideFcn = '';%开始训练网络 net = train(net, pn, tn);%使用训练好的网络,基于训练集的数据对BP网络进行仿真得到网络输出结果 %(因为输入样本(训练集)容量较少,否则一般必须用新鲜数据进行仿真测试) answer = sim(net, pn);%反归一化 answer1 = mapminmax('reverse', answer, outputStr);%绘制测试样本神经网络输出和实际样本输出的对比图(figure(1))------------------------------------------- t = 1990:2009;%测试样本网络输出客运量 a1 = answer1(1,:); %测试样本网络输出货运量 a2 = answer1(2,:);figure(1); subplot(2, 1, 1); plot(t, a1, 'ro', t, passengerVolume, 'b+'); legend('网络输出客运量', '实际客运量'); xlabel('年份'); ylabel('客运量/万人'); title('神经网络客运量学习与测试对比图'); grid on;subplot(2, 1, 2); plot(t, a2, 'ro', t, freightVolume, 'b+'); legend('网络输出货运量', '实际货运量'); xlabel('年份'); ylabel('货运量/万吨'); title('神经网络货运量学习与测试对比图'); grid on;%使用训练好的神经网络对新输入数据进行预测%新输入数据(2010年和2011年的相关数据) newInput = [73.39 75.55; 3.9635 4.0975; 0.9880 1.0268]; %利用原始输入数据(训练集的输入数据)的归一化参数对新输入数据进行归一化 newInput = mapminmax('apply', newInput, inputStr);%进行仿真 newOutput = sim(net, newInput);%反归一化 newOutput = mapminmax('reverse',newOutput, outputStr);disp('预测2010和2011年的公路客运量分别为(单位:万人):'); newOutput(1,:) disp('预测2010和2011年的公路货运量分别为(单位:万吨):'); newOutput(2,:)%在figure(1)的基础上绘制2010和2011年的预测情况------------------------------------------------------- figure(2); t1 = 1990:2011;subplot(2, 1, 1); plot(t1, [a1 newOutput(1,:)], 'ro', t, passengerVolume, 'b+'); legend('网络输出客运量', '实际客运量'); xlabel('年份'); ylabel('客运量/万人'); title('神经网络客运量学习与测试对比图(添加了预测数据)'); grid on;subplot(2, 1, 2); plot(t1, [a2 newOutput(2,:)], 'ro', t, freightVolume, 'b+'); legend('网络输出货运量', '实际货运量'); xlabel('年份'); ylabel('货运量/万吨'); title('神经网络货运量学习与测试对比图(添加了预测数据)'); grid on;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
5. 运行结果
预测2010和2011年的公路客运量分别为(单位:万人):
ans =
1.0e+04 *
4.4384 4.4656
预测2010和2011年的公路货运量分别为(单位:万吨):
ans =
1.0e+04 *
2.1042 2.1139
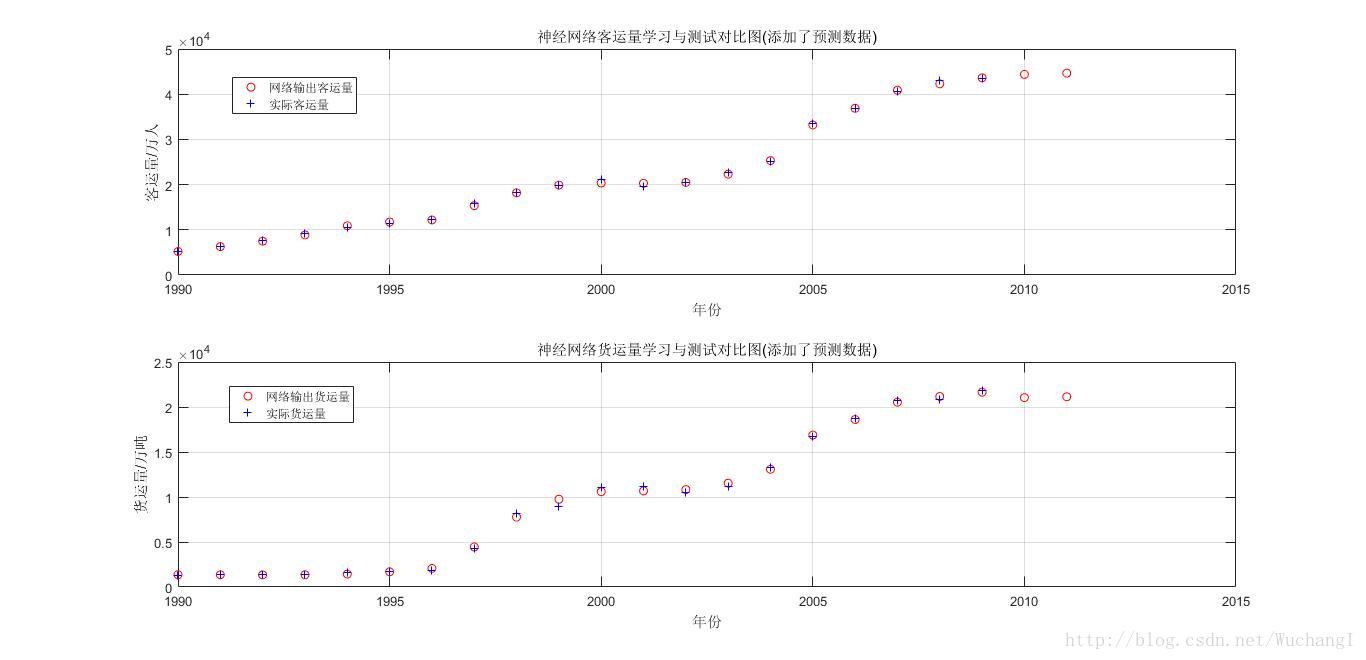
6. 绘制的图像
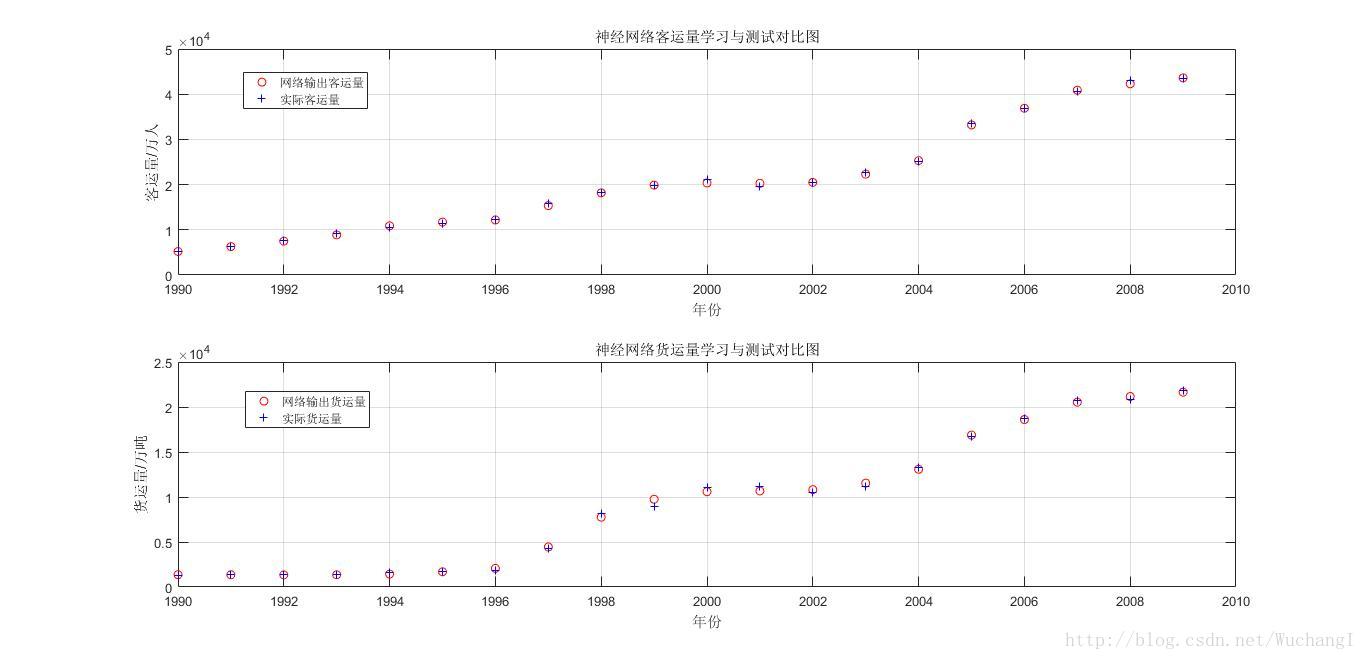
- figure(1)
- figure(2)
用MATLAB实现神经网络
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/549361.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Follow Me:CCIE RS--使用小凡模拟器搭建的CCIE拓扑图
我用小凡模拟器搭建了CCIE LAB 拓扑图有何不对的地方请指正转载于:https://blog.51cto.com/tanfo/216831
【积累】非常全面的开源数据集
非常全面的开源数据集 由skymind.ai公布 非常全面的开源数据集最近新增数据集自然图像数据集地理空间数据人工数据集人脸数据集视频数据集文本数据集问答数据集情感数据集推荐和排名系统语音数据集音符音乐数据集健康 &生物数据政府&统计数据网络和图形其它数据集 最近…
女性最常说的5大谎言:
女性最常说的5大谎言: “没事,我很好” “哦,这不是新买的,买很久了” “这不是很贵” “这是打折时买的” “我正在路上” 我好像都曾听过! 摘自:http://lady.163.com/special/00261MPK/kexue004.html
【资源】史上最全数据集汇总
无论是数据挖掘还是目前大热的深度学习,都离不开“大数据”。大公司们一般会有自己的数据,但对于创业公司或是高校老师、学生来说,“Where can I get large datasets open to the public” 是一个不得不面对的问题。 本文将为您提供一个网站/…
非线性最优化(二)——高斯牛顿法和Levengerg-Marquardt迭代
高斯牛顿法和Levengerg-Marquardt迭代都用来解决非线性最小二乘问题(nonlinear least square)。 From Wiki
The Gauss–Newton algorithm is a method used to solve non-linear least squares problems. It is a modification of Newtons method for finding a minimum of a …
为右键新建菜单添加内容
右键菜单的内容由注册表关联,通过修改注册表就可以定制鼠标右键快捷菜单中的“新建”菜单所包含的项目。 需要注意的是,在修改注册表以前要先将注册表备份,以免出现问题时无法恢复。 一、增加菜单项目1.首先,决定要增加到菜单中的…
逆透视变换详解 及 代码实现(一)
逆透视变换详解 及 代码实现(一) 中主要是原理的说明: 一、世界坐标轴和摄像机坐标轴
从下图中可以看到,世界坐标为(X,Y,Z) 相机坐标为(Xc,Yc,Zc)
而世界坐标变换到相机坐标存在一个旋转矩阵变换R以及一个位移变换T。 根据上图…
逆透视变换详解 及 代码实现(二)
根据 逆透视变换详解 及 代码实现(一)的原理
下面我用车上拍摄的车道图像,采用逆透视变换得到的图像,给出代码前我们先看下处理结果。 首先是原始图像: 下图为逆透视变换图像: 下面说具体的实现吧!!
一、…
[赵星理]《简单男人》--歌曲温暖你的心,激励你前进
简单的男人,简单的歌曲,赵星理《简单男人》送给所有身负家庭责任的人,要让家越来越美,再苦再累也不能后退。加油!简单男人词曲:赵星理演唱:赵星理累不累也不许落泪醉不醉苦辣都值得回味要让家越…
ArrayList list = new ArrayList(20);中的list扩充几次
16. ArrayList list new ArrayList(20);中的list扩充几次()
A 0 B 1 C 2 D 3
答案:A ArrayList动态扩容机制 初始化:有三种方式 默认的构造器,将会以默认的大小来初始化内部的数组:public …
利用ATL创建com组件和如何在程序中使用组件的接口函数和设置接口的属性
这是一个ATL开发实例的流程: 1. 在atl中插入一个atl实例,然后添加一个类,派生自ccmdtarget。 2. 添加相应的属性或者方法,在这里需要明白一点的是,这个属性和方法其实是一个概念,只是添加一个属…
java 课外练习题
1.下列哪些是Thread类中的方法()
A start() B run() C exit() D getPriority()
解析:线程的就绪状态:新建线程后start()方法的调用,来启动线程,但此时线程并没有进入运行状态,只是…
关于ubuntu 是否需要使用std::到问题。
首先是在ubuntu下编译c要使用g,比如 g -Wall 01knap2.cpp -o 01knap2 而如果是编译c语言文件的话则需要用 gcc -Wall 01knap2.c -o 01knap2 即可,g编译得到的是.cpp文件,而gcc编译得到的是.c文件。 第二个是关于是否能够直接使用cout&#…
对一道基础string题及其变式题的思考与解析
1、下面程序的运行结果是()(选择一项) String str1“hello”; String str2new String(“hello”); System.out.println(str1str2);
A.true
B.false
C.hello
D.he 答案:B 分析:str1没有使用new关键字&am…
Redo Log 和Checkpoint not complete
首先我们来看下 alertSID.log 日志: Mon Nov 30 17:31:54 2009 Thread 1 advanced to log sequence 14214 (LGWR switch) Current log# 3 seq# 14214 mem# 0: /u03/oradata/newccs/redo03.log Mon Nov 30 17:34:29 2009 Thread 1 advanced to log sequence 14215 (L…
组合数学中的项链计数
给c种不同颜色宝石能穿成多少种长度为s的宝石项链(本质不同) Burnside定理的应用: 当n为奇数时,有n种翻转,每种翻转都是以一个顶点和该顶点对边的中点对称。有k^(n/21)*n种。 当n为偶数时,有n种翻转&#x…
蓝桥杯 算法训练(四)结点选择(树形动态规划)
结点选择(树形动态规划)C语言 问题描述 有一棵 n 个节点的树,树上每个节点都有一个正整数权值。如果一个点被选择了,那么在树上和它相邻的点都不能被选择。求选出的点的权值和最大是多少? 输入格式 第一行包含一个整数…





——高斯牛顿法和Levengerg-Marquardt迭代)

)

)
![[赵星理]《简单男人》--歌曲温暖你的心,激励你前进](http://pic.xiahunao.cn/[赵星理]《简单男人》--歌曲温暖你的心,激励你前进)
;中的list扩充几次)







结点选择(树形动态规划))