Hanoi(汉诺)塔问题

问题描述：

Hanoi(汉诺)塔问题。古代有一个梵塔，塔内有3个座A,B,C，开始时A座有n个盘子，盘子大小不等，大的在下，小的在上。有一个老和尚想把这n个盘子，从A座移动到C座，但是每次只允许移动一个盘子，且在移动的过程中，3个座上都始终保持大盘在下，小盘在上。在移动的过程中，可以利用B座。

要求编程打印出移动的步骤~

问题分析：

当有1个盘子的时候，步骤：A->C；

当有2个盘子的时候，步骤：A->B  |  A->C  |  B->C；

当有3个盘子的时候，步骤：A->C  |  A->B  |  C->B  |  A->C  |  B->A  |  B->C  |  A->C;

分析了以上3个盘子的移动步骤，可以将移动n个盘子的步骤抽象为3个大的步骤；首先，将A上的上面的n-1个盘子都移动到B上，然后将B上的n-1个盘子移动到C上，然后将B上的n-1个盘子移动到C上。

示例代码：

/*汉诺塔问题*/
#include<iostream>
using namespace std;
void move(char x, char y){cout<<x<<"->"<<y<<endl; //执行移动的操作
}
void hnt(int n, char a, char b, char c){if(n==1)move(a,c);//当只移动一个盘子的时候，不需要借助第三个盘子else if(n>1){hnt(n-1,a,c,b);//需要借助汉诺塔函数，把A上面的n-1个盘子移动到B上move(a,c);//直接把第n个盘子移动到C上hnt(n-1,b,a,c);//借助汉诺塔函数，把B上的n-1个盘子移动到C上} 
} 
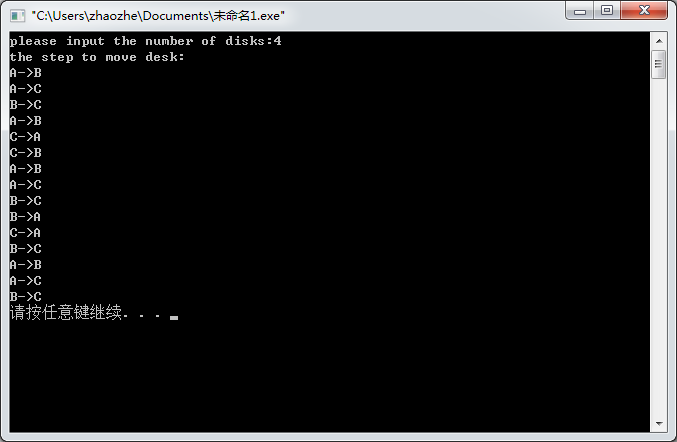
int main(){int n;cout<<"please input the number of disks:";cin>>n;cout<<"the step to move desk:"<<endl;hnt(n,'A','B','C');return 1;}

最后在上一个n=4的时候的截图

晚安啦~