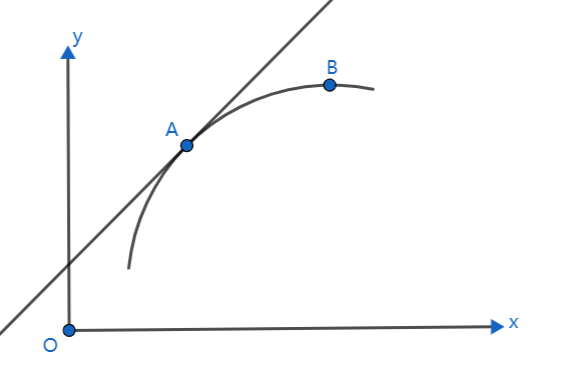
本文研究平面、空间直线在参数方程形式下,切线斜率(即导数)如何表示的问题。
如上图所示。 设 y = f ( x ) , x = φ ( t ) , y = ψ ( t ) 当 t = t 0 时, x = x 0 , y = y 0 ,即点 A 坐标为 ( x 0 , y 0 ) 点 A 处的导数 f ′ ( x 0 ) = lim Δ x → 0 Δ y Δ x = lim Δ t → 0 ψ ( t 0 + Δ t ) − ψ ( t 0 ) φ ( t 0 + Δ t ) − φ ( t 0 ) = lim Δ t → 0 ψ ( t 0 + Δ t ) − ψ ( t 0 ) Δ t / φ ( t 0 + Δ t ) − φ ( t 0 ) Δ t = lim Δ t → 0 ψ ( t 0 + Δ t ) − ψ ( t 0 ) Δ t / lim Δ t → 0 φ ( t 0 + Δ t ) − φ ( t 0 ) Δ t = ψ ′ ( t 0 ) φ ′ ( t 0 ) 因此点 A 处的切线向量可表示为 ( ψ ′ ( t 0 ) , φ ′ ( t 0 ) ) 而切线方程为 y − y 0 = ψ ′ ( t 0 ) φ ′ ( t 0 ) ( x − x 0 ) ,即 y − y 0 ψ ′ ( t 0 ) = x − x 0 φ ′ ( t 0 ) 同理可得空间直线的点向式方程为: y − y 0 ψ ′ ( t 0 ) = x − x 0 φ ′ ( t 0 ) = z − z 0 ω ′ ( t 0 ) 如上图所示。\\ 设y=f(x),x=\varphi(t),y=\psi(t) \\ 当t=t_0时,x=x_0,y=y_0,即点A坐标为(x_0,y_0) \\ 点A处的导数f^\prime(x_0)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\varphi(t_0+\Delta t)-\varphi(t_0)} \\ \,\\ =\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\Delta t}/\frac{\varphi(t_0+\Delta t)-\varphi(t_0)}{\Delta t} \\ \,\\ =\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\Delta t}/\lim_{\Delta t \to 0}\frac{\varphi(t_0+\Delta t)-\varphi(t_0)}{\Delta t} \\ \,\\ =\frac{\psi^\prime(t_0)}{\varphi^\prime(t_0)} \\ \,\\ 因此点A处的切线向量可表示为(\psi^\prime(t_0),\varphi^\prime(t_0)) \\ 而切线方程为y-y_0=\frac{\psi^\prime(t_0)}{\varphi^\prime(t_0)}(x-x_0),即\frac{y-y_0}{\psi^\prime(t_0)}=\frac{x-x_0}{\varphi^\prime(t_0)} \\ \,\\ 同理可得空间直线的点向式方程为:\\ \frac{y-y_0}{\psi^\prime(t_0)}=\frac{x-x_0}{\varphi^\prime(t_0)}=\frac{z-z_0}{\omega^\prime(t_0)} 如上图所示。设y=f(x),x=φ(t),y=ψ(t)当t=t0时,x=x0,y=y0,即点A坐标为(x0,y0)点A处的导数f′(x0)=Δx→0limΔxΔy=Δt→0limφ(t0+Δt)−φ(t0)ψ(t0+Δt)−ψ(t0)=Δt→0limΔtψ(t0+Δt)−ψ(t0)/Δtφ(t0+Δt)−φ(t0)=Δt→0limΔtψ(t0+Δt)−ψ(t0)/Δt→0limΔtφ(t0+Δt)−φ(t0)=φ′(t0)ψ′(t0)因此点A处的切线向量可表示为(ψ′(t0),φ′(t0))而切线方程为y−y0=φ′(t0)ψ′(t0)(x−x0),即ψ′(t0)y−y0=φ′(t0)x−x0同理可得空间直线的点向式方程为:ψ′(t0)y−y0=φ′(t0)x−x0=ω′(t0)z−z0
专题:平面、空间直线参数方程下的切线斜率问题
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/54700.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
为Claude的分析内容做准备:提取PDF页面内容的简易应用程序
由于Claude虽然可以分析整个文件,但是对文件的大小以及字数是有限制的,为了将pdf文件分批传入Claude人工智能分析和总结文章内容,才有了这篇博客: 在本篇博客中,我们将介绍一个基于 wxPython 和 PyMuPDF 库编写的简易的…
【电路设计】单节锂电池使用
前言 最近在研究如何利用单节锂电池给3.3V单片机供电。
找到两个比较好的教程 单节锂电池如何转3.3V?升压还是降压? 锂电池接了保护板,就可以用五伏电压直接充电了吗?
其中上面提到的LDO,这里有一个型号࿱…
【校招VIP】测试专业课之TCP/IP模型
考点介绍: 大厂测试校招面试里经常会出现TCP/IP模型的考察,TCP/IP协议是网络基础知识,但是在校招面试中很多同学在基础回答中不到位,或者倒在引申问题里,就丢分了。
『测试专业课之TCP/IP模型』相关题目及解析内容可点…
TypeScript数组和对象的操作
TypeScript数组和对象的操作 一、数组的声明二、数组初始化三、数组元素赋值、添加、更改四、删除五、合并、断开数组六、查找数组元素位置七、连接数组元素八、排序、反序数组九、遍历请看这里 一、数组的声明
let arr1: Array<number>;
let arr2: number[];二、数组初…
Property ‘sqlSessionFactory‘ or ‘sqlSessionTemplate‘ are required
项目场景:
最近因为公司业务需要在搭一个新架构,用的springboot3和jdk17,在整合mybatis多数据源的时候报错 (引用的mybatisplus 和 mybatisplusjion的是最新的包-2023-08-26) Error creating bean with name ‘XXXServiceImpl’:…
有限与无限游戏 | 真北荐书
2023佛山敏捷之旅暨DevOps Meetup志愿者为进行大会的组织与准备,每周三晚有一个例会。 例会前等人的时间,涌现出一个小的分享环节。今天分享这本书:《有限与无限游戏》。 大家选择成为志愿者,是一个无限游戏。而组织活动和完成各种…
一文讲清楚c/c++中的宏
一文讲清楚c/c中的宏 文章目录 一文讲清楚c/c中的宏一、如何理解这个“宏”字面的意思呢?二、c/c中的宏详解三、宏的使用场景 一、如何理解这个“宏”字面的意思呢? 在刚开始学习C语言的时候,始终有点分不清楚"宏"这个字面上的意思…
设计模式-责任链模式
原理和实现
将这些接收对象串成一条链,并沿着这条链传递这个请求,直到链上的某个接收 对象能够处理它为止,实时上,在常见的使用场景中,我们的责任链并不是和概念中的完全一样 ● 原始概念中,是直到链上的某…
Python|OpenCV-读取视频,显示视频并保存视频(3)
前言 本文是该专栏的第3篇,后面将持续分享OpenCV计算机视觉的干货知识,记得关注。
在使用OpenCV处理视频的时候,不论是摄像头画面还是视频文件,通常情况下都要使用VideoCapture类来进行每一帧图像的处理。对于OpenCV而言,只要使用视频文件作为参数,它就可以打开视频文件…
在前端开发中,什么叫移动设备上的视口?如何通过header标签中的meta属性设置页面的视口。
移动设备上的视口(Viewport)是指在移动设备上可见的网页区域。由于移动设备的屏幕尺寸和分辨率各不相同,为了确保网页在各种设备上都能正确显示和交互,需要通过视口设置来适配不同的屏幕尺寸。
在移动设备上,网页通常…
Qt XML文件解析 QDomDocument
QtXml模块提供了一个读写XML文件的流,解析方法包含DOM和SAX,两者的区别是什么呢?
DOM(Document Object Model):将XML文件保存为树的形式,操作简单,便于访问。
SAX(Simple API for …
SpringBoot2.0集成WebSocket
<!-- websocket --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId></dependency>
新建配置类
import org.springframework.boot.autoconfigure.condition.Cond…
视频监控/视频集中存储/云存储平台AI智能分析网关V3——功能简介
安防监控/视频集中存储/云存储平台AI智能分析网关V3内置了20多种AI算法,可针对安全生产、通用园区、智慧食安、石油化工等场景,提供基于视频智能检测技术的个性化行业解决方案。今天来具体介绍下v3版本的智能分析网关有哪些算法功能配置。 一、硬件
安防…
DDR与PCIe:高性能SoC的双引擎
SoC芯片无处不在,小到家电控制的MCU,大到手机芯片,我们都会接触到。如今大部分芯片设计公司都在开发SoC芯片,一颗SoC芯片可以集成越来越多的功能,俨然它已成为IC设计业界的焦点。
高性能、高速、高带宽的互联和存储的…
深入分析负载均衡情景
本文出现的内核代码来自Linux5.4.28,为了减少篇幅,我们尽量不引用代码,如果有兴趣,读者可以配合代码阅读本文。
一、有几种负载均衡的方式?
整个Linux的负载均衡器有下面的几个类型: 实际上内核的负载均衡…
Git push拦截
遇到的问题
今天想提交代码到gitee,结果发现被拦截了,有段提示“forbidden by xxxx”… 我记得xxxx好像是公司的一个防泄密的东西… 这个东西是怎么实现的呢?
解决
原来git提供很多hook,push命令就有一个pre-push的hook&#x…
如何保障Facebook账号登录稳定
当谈到保障Facebook账号的稳定性时,我们不得不提到那些令人头疼的情况——Facebook账号被封。尽管我们已经踏入数字化的未来,但是被封号似乎是一个时常困扰着社交媒体用户的问题。那么,让我们来看看一些常见的Facebook账号被封的原因…
《C和指针》笔记13: static关键字总结
这里对static关键字做一下总结,可以回顾一下前面两篇博客的文章。
《C和指针》笔记11: external和internal链接属性 《C和指针》笔记12: 存储类型(自动变量、静态变量和寄存器变量)
当它用于函数定义时,或用于代码块之外的变量声…
Python Requests模块session的使用建议
本篇主要讲解Python Requests模块session的使用建议及整个会话中的所有cookie的方法。
测试代码
服务端:下面是用flask做的一个服务端,用来设置cookie以及打印请求时的请求头。
# -*- coding: utf-8 -*-
from flask import Flask, make_response, req…









)









