回溯算法n皇后问题

N-皇后问题 (N - Queen's problem)

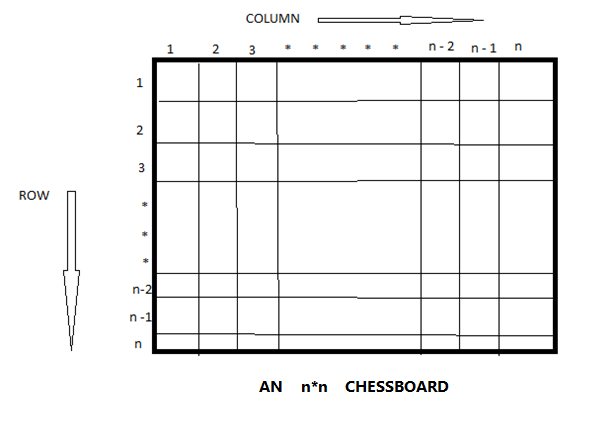
The n – queen problem is the generalized problem of 8-queens or 4 – queen’s problem. Here, the n – queens are placed on a n * n chess board, which means that the chessboard has n rows and n columns and the n queens are placed on thus n * n chessboard such that no two queens are placed in the same row or in the same column or in same diagonal. So that, no two queens attack each other.

n皇后问题是8皇后或4 皇后问题的广义问题 。 在这里，将n –皇后放置在* n棋盘上，这意味着该棋board具有n行和n列，并且将n个皇后放置在n * n棋盘上，这样就不会在同一行中放置两个皇后。在同一列或同一对角线中。 因此，没有两个女王互相攻击。

Here, we suppose that the queen i is to be placed in row i. We can say that 1 queen is placed in the first row only but can have columns from 1, 2... n so that they satisfy all the explicit and implicit constraints.

在这里，我们假设将女王i放在第i行。 我们可以说1个皇后只放在第一行，但是可以有1、2 ... n个列，这样它们就可以满足所有显式和隐式约束。

All solutions to the n – queen’s problem can be therefore represented as n – tuples (x1, x2... xn) where xi is the column on which queen i is to be placed.

因此，n- 皇后问题的所有解决方案都可以表示为n-元组(x1，x2 ... xn)，其中xi是放置女王i的列。

The explicit constraints using this formulation are Si = {1, 2, 3... n-1, n}, where 1 <= I <= n. Therefore, the solution space consists of nˆn n- tuples. Now, while considering the implicit constraints, that no two xi’s can be same i.e., two queens cannot be in the same row, same column, or in same diagonal. So, each xi should be different. Now by the above constraint, the solution is the permutations of the n – tuples (1, 2, 3, 4... n-1, n).

使用此公式的显式约束为Si = {1,2,3 ... n-1，n}，其中1 <= I <= n。 因此，解空间由nˆn个元组组成。 现在，在考虑隐式约束时，没有两个xi可以相同，即两个皇后不能在同一行，同一列或同一对角线中。 因此，每个xi应该不同。 现在，根据上述约束，解决方案是n个元组的排列(1、2、3、4 ... n-1，n)。

算法 (Algorithm )

For all the solutions of the n - queen’s problem...

对于n-皇后问题的所有解...

1.	Algorithm N Queen (k, n)
2.	// Using backtracking, this procedure prints all possible placements of
3.	// n- queens on the n*n chess board so that they are non-attacking.
4.	{
5.	For I = 1 to n do
6.	{
7.	If Place (k, i) then
8.	{
9.	X[k] = I;
10.	If (k = n) then write (x[1: n ]) ;
11.	 Else N Queens (k+1, n);
12.	}
13.	}
14.	}

翻译自: https://www.includehelp.com/algorithms/n-queens-problem-and-solution-using-backtracking-algorithm.aspx

回溯算法n皇后问题