二进制补码乘法除法
1)二进制乘法 (1) Binary Multiplication)
Binary numbers can be multiplied using two methods,
二进制数可以使用两种方法相乘,
Paper method: Paper method is similar to multiplication of decimal numbers on paper.
纸张方法:纸张方法类似于纸张上十进制数字的乘法。
Computer method: Computer method is used by digital machines to multiply the binary numbers.
计算机方法:数字计算机使用计算机方法乘以二进制数。
However, both these methods follow the same rule of multiplication which is,
但是,这两种方法都遵循相同的乘法规则,即
0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1
Note: If two binary numbers are of 'n' bits each in magnitude, then their product can be maximum '2n' bits long in magnitude.
注意:如果两个二进制数的大小均为'n'位,则它们的乘积最大为'2n'位。
长手乘法/纸张方法 (Long Hand Multiplication/Paper Method)
The long Hand Multiplication technique is similar to decimal multiplication that we do on paper.
长手乘法技术类似于我们在纸上进行的十进制乘法。
In this technique, we multiply the multiplicand with each bit of multiplier and add the partial products together to obtain the result.
在这项技术中,我们将被乘数与乘数的每一位相乘,并将部分乘积相加以获得结果。
We scan the multiplier from the RHS, if the multiplier bit is 1 then we copy the whole multiplicand in the partial product and if the multiplier bit is 0, we replace all the bits of the multiplicand with 0 in the partial product.
我们从RHS扫描乘数,如果乘数位为1,则复制部分乘积中的整个被乘数,如果乘数位为0,则将乘积中的所有位替换为部分乘积中的0。
Example 1: Compute (10)2 * (11)2
示例1:计算(10) 2 *(11) 2
Solution:
解:
Therefore, the result is (10)2 * (11)2 = (110)2
因此,结果是(10) 2 *(11) 2 =(110) 2
Verification:
验证:
We can verify our result by converting the binary numbers to respective decimal numbers and multiplying them to get the result.
我们可以通过将二进制数字转换为相应的十进制数字并乘以它们以获得结果来验证我们的结果。
Here, (10)2 = (2)10, (11)2 = (3)10 and (110)2 = (6)10. When we will multiply 2 and 3, we will get the product as 6, which we are getting by multiplication of binary numbers. Hence our solution is correct.
在此, (10) 2 =(2) 10 , (11) 2 =(3) 10和(110) 2 =(6) 10 。 当我们将2和3相乘时,我们将得到乘积为6 ,这是通过二进制数相乘得到的。 因此,我们的解决方案是正确的。
Example 2: Compute (111)2 * (101)2
示例2:计算(111) 2 *(101) 2
Solution:
解:
Therefore, the result is (111)2 * (101)2 = (100011)2
因此,结果为(111) 2 *(101) 2 =(100011) 2
Example 3: Compute (1010.01)2 * (1.01)2
示例3:计算(1010.01) 2 *(1.01) 2
Solution:
解:
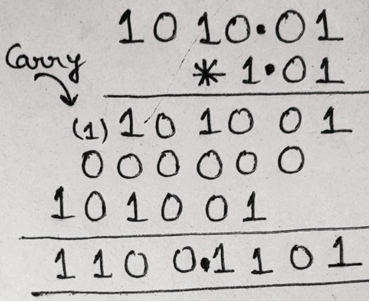
Therefore, the result is (1010.01)2 * (1.01)2 = (1100.1101)2
因此,结果为(1010.01) 2 *(1.01) 2 =(1100.1101) 2
2)二进制除法 (2) Binary Division)
Like binary multiplication, division of binary numbers can also be done in two ways which are:
像二进制乘法一样,二进制数的除法也可以通过两种方式完成:
Paper Method: Paper Method division of binary numbers is similar to decimal division.
纸张方法 :纸张方法对二进制数的除法类似于十进制除法。
Computer Method: Computer Method is used by the digital devices where they make use of 2's complement of a number to subtract the numbers during division.
计算机方法 :数字设备使用数字方法使用数字的补码来在除法运算中减去数字。
长手分割法/纸法 (Long Hand Division Method/Paper Method)
In binary division, there are only two possibilities either 0 or 1. If the divisor goes into the dividend then quotient will be 1 and if the divisor doesn’t then the quotient will be 0. Similar, to decimal division, we will subtract divisor from the dividend and the result will be appended by the next bit in the dividend. This process repeats until all the bits of the dividend are considered.
在二进制除法中 ,只有两种可能性,即0或1。如果除数进入被除数,则商将为1;如果除数没有,则商将为0。类似于十进制除法,我们将减去除数的红利和结果将被添加到红利的下一位。 重复此过程,直到考虑了除数的所有位。
Example 1: Divide (111101)2 by (100)2
范例1:将(111101) 2除以(100) 2
Solution:
解:
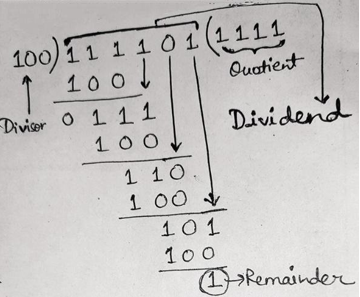
Therefore, the result is (111101)2 / (100)2 gives (1111)2 (Quotient) and 1 (Remainder)
因此,结果为(111101) 2 /(100) 2得出(1111) 2 (商)和1(余数)
Example 2: Divide (110101.11)2 by (101)2
范例2:将(110101.11) 2除以(101) 2
Solution:
解:
Therefore, the result is (110101.11)2 / (101)2 gives (1010.11)2.
因此,结果为(110101.11) 2 /(101) 2给出(1010.11) 2 。
Verification:
验证:
We can verify our result by converting the binary numbers to respective decimal numbers and then dividing the dividend by the divisor to get the result.
我们可以通过将二进制数字转换为相应的十进制数字,然后将除数除以除数来得到结果,从而验证我们的结果。
Here, (110101.11)2 = (53.75)10, (101)2 = (5)10 and (1010.11)2 = (10.75)10. When we will divide 53.75 by 5, we will get the result as 10.75, which we are getting by doing division of binary numbers. Hence our solution is correct.
在此, (110101.11) 2 =(53.75) 10 , (101) 2 =(5) 10和(1010.11) 2 =(10.75) 10 。 当我们将53.75除以5时 ,将得到10.75的结果,这是通过对二进制数进行除法得到的。 因此,我们的解决方案是正确的。
Example 3: Divide (1010.1)2 by (101.01)2
示例3:将(1010.1) 2除以(101.01) 2
Solution:
解:
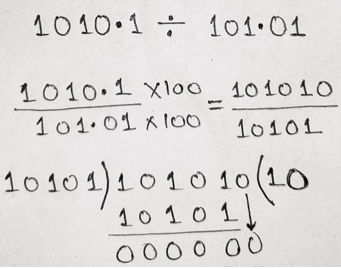
Therefore, the result is (1010.1)2 / (101.01)2 gives (10)2.
因此,结果是(1010.1)2 /(101.01)2给出了(10)2。
翻译自: https://www.includehelp.com/basics/binary-multiplication-and-division.aspx
二进制补码乘法除法










方法以及Ruby中的示例)

函数与示例)


方法与示例)


函数)
