哈密顿路径_检查图形是否为哈密顿量（哈密顿路径）

哈密顿路径

Problem Statement:

问题陈述：

Given a graph G. you have to find out that that graph is Hamiltonian or not.

给定图G。您必须找出该图是否为哈密顿量 。

Example:

例：

Input:

输入：

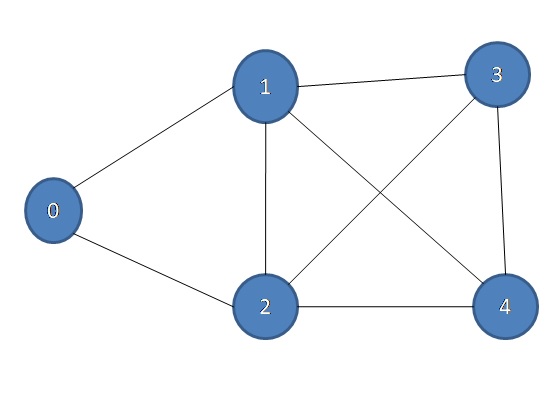
Output: 1

输出1

Because here is a path 0 → 1 → 5 → 3 → 2 → 0 and 0 → 2 → 3 → 5 → 1 → 0

因为这里是路径0→1→5→3→2→0和0→2→3→5→1→0

Algorithm:

算法：

To solve this problem we follow this approach:

为了解决这个问题，我们采用以下方法：

We take the source vertex and go for its adjacent not visited vertices.
我们获取源顶点，并寻找其相邻的未访问顶点。
Whenever we find a new vertex we make it source vertex and we repeat step 1.
每当我们找到一个新顶点时，就将其设为源顶点，然后重复步骤1。
When a vertex count is equal to the vertex number then we check that from vertex is there any path to the source vertex. If there is exist a path to the source vertex then we will mark it and if not then make that vertex as unmarked and continue the process.
当顶点数等于顶点数时，我们检查从顶点开始是否存在到源顶点的任何路径。如果存在到源顶点的路径，那么我们将对其进行标记，如果没有，则将该顶点设为未标记并继续该过程。
If there is no such path then we say NO.
如果没有这样的路径，那么我们说不。

检查图是否为哈密顿的C ++实现 (C++ Implementation to check a graph is Hamiltonian or not )

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
void addedge(list<int>* g, int u, int v)
{
g[u].push_back(v);
g[v].push_back(u);
}
int hamiltonian(list<int>* g, int v, int s, int& count, bool* vis, int& h)
{
if (count > 1 && s == 0) {
h = 1;
return 1;
}
list<int>::iterator it;
for (it = g[s].begin(); it != g[s].end(); it++) {
if (!vis[*it]) {
vis[*it] = true;
count++;
if (count == v) {
vis[0] = false;
}
hamiltonian(g, v, *it, count, vis, h);
vis[0] = true;
vis[*it] = false;
count--;
}
}
return 0;
}
int main()
{
int num;
cin >> num;
for (int i = 0; i < num; i++) {
int v, e;
cin >> v >> e;
list<int> g[v];
int x, y;
for (int j = 0; j < e; j++) {
cin >> x >> y;
addedge(g, x, y);
}
bool vis[v];
memset(vis, false, sizeof(vis));
int count = 1;
vis[0] = true;
int h = 0;
hamiltonian(g, v, 0, count, vis, h);
cout << h << endl;
}
return 0;
}

Output

输出量