计算理论 形式语言与自动机

Pushdown Automaton (PDA) is a kind of Automaton which comes under the theory of Computation that appoints stack. The word Pushdown stands due to the fact that the stack can be pushed down as operations can only work on the elements which are on the top of the stack. A PDA can store an infinite amount of information. It is used to identify Context-free languages.

下推式自动机(Pushdown Automaton，PDA)是一种基于计算理论的自动机，它指定堆栈。 之所以使用Pushdown一词，是因为可以将堆栈向下推，因为操作只能在堆栈顶部的元素上进行。 PDA可以存储无限量的信息。 它用于识别上下文无关的语言。

The following equation will help you to understand Pushdown Automaton (PDA),

以下等式将帮助您了解下推自动机(PDA) ，

"Pushdown Automation" = "Finite State Machine" + "Stack"

“下推式自动化” =“有限状态机” +“堆栈”

A finite state machine does not employ any stack and only bothers about the input signal and the current state that does not work in the case of context free grammar. Push Down Automata is different from finite state machine because,

有限状态机不使用任何堆栈，而只关心输入信号和当前状态，这在上下文无关文法的情况下不起作用。 下推自动机与有限状态机不同，因为，

1. It uses top of the stack for deciding which transition is to be taken.

   它使用堆栈的顶部来决定要进行的过渡。

2. While performing the transition, it can handle or manipulate the stack.

   在执行过渡时，它可以处理或操纵堆栈。

Pushdown Automaton (PDA) reads the provided string from left to right direction. The current state, input symbol and the symbol at TOS (Top of the Stack) are being indexed in the table and helps in choosing a transition, this happens at each step. While performing a transition, PDA can manipulate stack in two ways, either it can push a symbol at the top of the stack or can pop out a symbol from the stack.

下推式自动机(PDA)从左到右读取提供的字符串。 在表中为当前状态，输入符号和TOS(堆栈顶部)上的符号建立索引，并有助于选择过渡，这在每个步骤中都会发生。 在执行转换时，PDA可以通过两种方式操纵堆栈，既可以将符号推入堆栈的顶部，也可以从堆栈弹出符号。

Formal definition of PDA,

PDA的正式定义，

PDA can be betokened formally by a 7-tuple (Q, ∑, S, δ, q0, I, F) where,

PDA可以由7个元组(Q，∑，S，δ，q0，I，F)正式标记，其中，

1. Q is the number of states. It is finite.

   Q是状态数。 这是有限的。

2. ∑ is an input alphabet. It is a finite set.

   Σ是输入字母。 这是一个有限集。

3. S stands for stack symbols.(which can be pushed and popped from the stack).

   S代表堆栈符号(可以从堆栈中压入和弹出)。

4. δ is the transition function which is Q × (∑ ∪ {ε}) × S × Q × S*. It is a finite subset.

   δ是转移函数Q×(∑ε{ε})×S×Q×S * 。 它是一个有限子集。

5. q0 is the start or initial or beginning state (q0 ∈ Q).

   q0是开始或初始或开始状态(q0∈Q) 。

6. I is the initial stack top symbol (I ∈ S).

   I是初始堆栈顶部符号(I∈S) 。

7. F is the set of accepting states (F ∈ Q).

   F是一组接受状态(F∈Q) 。

In a specified state, PDA will read the symbol which is at the top of the stack and the input signal and move to a new state after changing the symbol of the stack.

在指定状态下， PDA将读取堆栈顶部的符号和输入信号，并在更改堆栈符号后移至新状态。

Consider the following diagram which demonstrates transition in a PDA, from State q1 to state q2 described as x, y->z.

考虑下图，该图演示了PDA从状态q1到状态q2的过渡，描述为x，y-> z 。

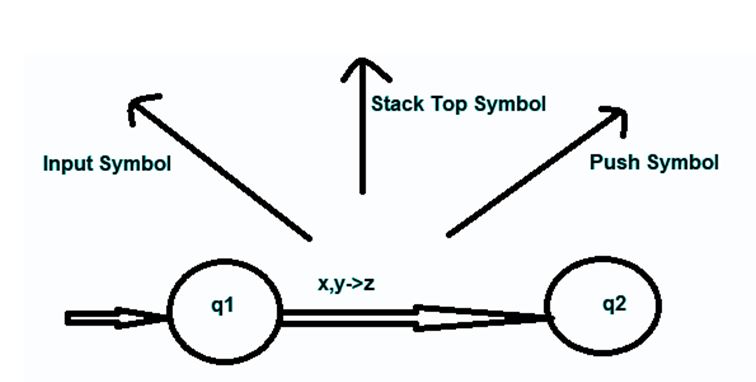
In the above scenario, you can observe that if the current state of machine is q1, The input symbol is 'x' and 'y' is at the Top of Stack symbol then we can carry out push and pop operation by popping 'y' and pushing 'z' on the top of the stack and can proceed to state q2.

在上述情况下，您可以观察到，如果计算机的当前状态为q1 ，输入符号为'x'并且'y'在堆栈顶部符号中，那么我们可以通过弹出'y'来执行推入和弹出操作并将'z'推入堆栈的顶部，然后可以进入状态q2 。

Some important points of PDA:

PDA的一些要点：

• A PDA is used to check whether a given grammar is context free grammar or not.

  PDA用于检查给定的语法是否为上下文无关的语法。

• A grammar is accepted if it reaches the end state on using of all its input symbols.

  如果语法在使用所有输入符号时都达到结束状态，则该语法被接受。

• There are some other notations of the PDA that are used. They are:

  使用了PDA的其他一些符号。 他们是：

  1. Instantaneous Description: For a PDA, instantaneous description is given by,即时描述 ：对于PDA，即时描述由，

  2.     triplet (q,w,s), where 
     q is the current state of the machine
     w is the set of input symbols that are remaining
     s is the stack. 
     
     

  3. Turnstile Notation: It defines the moves of PDA based on ID notation. Transition is defined as 旋转记号 ：它根据ID记号定义PDA的移动。 过渡定义为'⊢'“⊢”

翻译自: https://www.includehelp.com/toc/pushdown-automaton-pda-theory-of-computation.aspx

计算理论 形式语言与自动机