将八进制数制转换为二进制，十进制和十六进制数制

1)将八进制数制转换为二进制数制 (1) Conversion of Octal Number System to Binary Number System)

To convert octal numbers into binary numbers, we can use the relationship between octal and binary numbers.

要将八进制数转换为二进制数，我们可以使用八进制数和二进制数之间的关系。

Octal Number	Binary Number
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

八进制数	二进制数
0	000
1个	001
2	010
3	011
4	100
5	101
6	110
7	111

Example 1: Convert (73.2)₈ into ( ? )₂

示例1：将(73.2) ₈转换为(？) ₂

Solution:

解：

Using the table provided above, we can replace octal numbers with their equivalent binary digits.

使用上面提供的表，我们可以将八进制数字替换为其等效的二进制数字。

    7 = 111
3 = 011
2 = 010

Therefore, (73.2)₈ = (111 011.010)₂

因此， (73.2) ₈ =(111 011.010) ₂

Example 2: Convert (475.62)₈ into ( ? )₂

示例2：将(475.62) ₈转换为(？) ₂

Solution:

解：

Using the table provided above, we can replace octal numbers with their equivalent binary digits.

使用上面提供的表，我们可以将八进制数字替换为其等效的二进制数字。

Therefore, (475.62)₈ = (100 111 101.110 010)₂

因此， (475.62) ₈ =(100111 101.110 010) ₂

2)将八进制数制转换为十进制数制 (2) Conversion of Octal Number System to Decimal Number System)

Conversion of octal number into a decimal number can be done using the positional weights by multiplying the positional weights with the corresponding bit and add them all together to obtain the decimal number.

可以使用位置权重将八进制数转换为十进制数，方法是将位置权重乘以相应的位，然后将它们全部加在一起以获得十进制数。

In an integral part of the octal number, the weights follow the pattern as 8⁰, 8¹, 8², 8³, 8⁴, 8⁵ and so on from right to left.
在八进制数的一个组成部分，权重按照图案作为8 ^0，8 ^1，8 ^2，8 ^3，8 ^4，8 ⁵等从右到左。
In the fractional part of the octal number, the weights follow the pattern as 8^-1, 8^-2, 8^-3, 8^-4, 8^-5 and so on from left to right.
在八进制数的小数部分，权重按照图案作为8 ^-1，8 ^{^-2，-3} 8，8 ^{^-4，-5} 8等从左到右。

Example 1: Convert (75.3)₈ = ( ? )₁₀

示例1：转换(75.3) ₈ =(？) ₁₀

Solution:

解：

octoal to decimal conversion (example 1)

We multiply each bit with the corresponding positional weight and then add them together to get the result.

我们将每个位乘以相应的位置权重，然后将它们加在一起以获得结果。

Therefore, (75.3)₈ = (61.375)₁₀

因此， (75.3) ₈ =(61.375) ₁₀

Example 2: Convert (624.712)₈ = ( ? )₁₀

示例2：转换(624.712) ₈ =(？) ₁₀

Solution:

解：

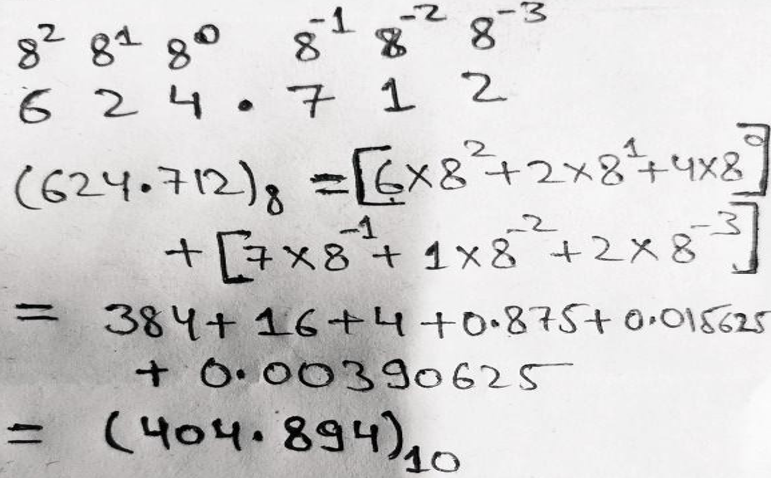
octoal to decimal conversion (example 2)

We multiply each bit with the corresponding positional weight and then add them together to get the result.

我们将每个位乘以相应的位置权重，然后将它们加在一起以获得结果。

Therefore, (624.712)₈ = (404.894)₁₀

因此， (624.712) ₈ =(404.894) ₁₀

Example 3: Convert (482.31)₈ = ( ? )₁₀

示例3：转换(482.31) ₈ =(？) ₁₀

Solution:

解：

Given number (482.31)₈ is not an octal number as a range of octal number is from 0 to 7 and the given number includes 8. So, it cannot be converted to a decimal number.

给定数字(482.31) ₈不是八进制数字，因为八进制数字的范围是从0到7，并且给定数字包括8。因此，不能将其转换为十进制数字 。

3)将八进制数制转换为十六进制数制 (3) Conversion of Octal Number System into Hexadecimal Number System)

Conversion of the octal number to hexadecimal can only be done using a certain definite path. We first have to convert octal number to binary number and then convert the binary number into hexadecimal number i.e., Octal Number → Binary Number → Hexadecimal Number

八进制数到十六进制的转换只能使用某个确定的路径来完成。我们首先必须将八进制数转换为二进制数，然后将二进制数转换为十六进制数，即八进制数→二进制数→十六进制数

Example 1: Convert (35.7)₈ into ( ? )₁₆

示例1：将(35.7) ₈转换为(？) ₁₆

Solution:

解：

Step 1: Convert octal number to binary number.
Therefore, (35.7)₈ = (011101.111)₂

步骤1：将八进制数转换为二进制数。
因此， (35.7) ₈ =(011101.111) ₂

Step 2: Convert binary number to a hexadecimal number.
Therefore, (011101.111)₂ = (1D.E)₁₆

步骤2：将二进制数转换为十六进制数。
因此， (011101.111) ₂ =(1D.E) ₁₆

Therefore, (35.7)₈ = (1D.E)₁₆

因此， (35.7) ₈ =(1D.E) ₁₆

Note: To know how to convert the binary number into a hexadecimal number?, Read: Conversion of binary number into a hexadecimal number.